Шлицы тензорного продукта хорошо подходят для данных с сеткой (двухмерные и даже многомерные). Для работы с разрозненными двумерными данными панель инструментов предоставляет сглаживающий шлиц тонкой пластины. Предположим, что заданы значения данных y(j) на разрозненных узлах данных x(:,j), j=1:N, в самолете. Чтобы привести конкретный пример,
n = 65; t = linspace(0,2*pi,n+1); x = [cos(t);sin(t)]; x(:,end) = [0;0];
обеспечивает 65 площадок, а именно 64 точки, равноудаленные на единичной окружности, плюс центр этой окружности. Вот соответствующие значения данных, а именно шумные значения очень хорошей функции.![]()
y = (x(1,:)+.5).^2 + (x(2,:)+.5).^2; noisy = y + (rand(size(y))-.5)/3;
Затем можно вычислить разумное приближение к этим данным с помощью
st = tpaps(x,noisy);
и постройте график результирующего приближения вместе с шумными данными
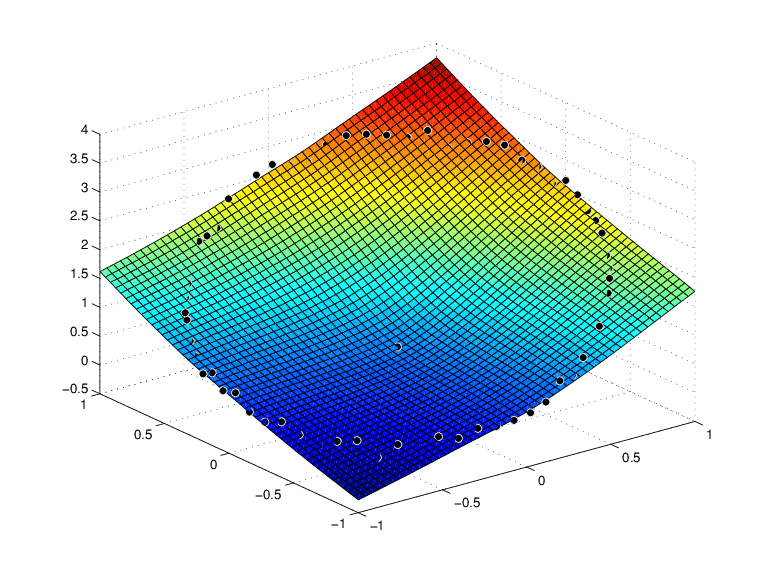
fnplt(st); hold on plot3(x(1,:),x(2,:),noisy,'wo','markerfacecolor','k') hold off
и таким образом создать следующую картину:
Тонколистовой сглаживающий сплайн аппроксимация шумных данных