Фитинг с наименьшими квадратами

Введение

Программа Curve Fitting Toolbox™ использует метод наименьших квадратов при подборе данных. Для подгонки требуется параметрическая модель, которая связывает данные ответа с данными предиктора с одним или несколькими коэффициентами. Результатом процесса подгонки является оценка коэффициентов модели.

Для получения оценок коэффициентов метод наименьших квадратов минимизирует суммированный квадрат остатков. Остаточное значение для i-ой точки ri данных определяется как разность между наблюдаемым значением _yi отклика и соответствующим значением _ŷi отклика и идентифицируется как ошибка, связанная с данными.

$\begin{array}{l} _{ri} =_{} {\overset{}{yi}}_{-} \\ y ^iresidual = \end{array}$ данные − подгонка

Суммируемый квадрат остатков задаётся как

$_{}^{}_{}^{}_{}^{S=∑i=1nri2=∑i=1n} {(_{} yi {\bar{}}_{} y}^{}$ ^ i) 2

где n - количество точек данных, включенных в аппроксимацию, а S - сумма оценок ошибок квадратов. Поддерживаемые типы фитинга с наименьшими квадратами включают в себя:

Линейные наименьшие квадраты
Взвешенные линейные наименьшие квадраты
Надежные наименьшие квадраты
Нелинейные наименьшие квадраты

Распределения ошибок

При подборе данных, содержащих случайные вариации, существуют два важных предположения, которые обычно делаются относительно ошибки:

Ошибка существует только в данных ответа, а не в данных предиктора.
Ошибки являются случайными и следуют нормальному (гауссову) распределению с нулевым средним и постоянной дисперсией, start2.

Второе предположение часто выражается как

$error∼N (0,^{}$ start2)

Предполагается, что ошибки обычно распределяются, поскольку нормальное распределение часто обеспечивает адекватное приближение к распределению многих измеренных величин. Хотя метод подгонки методом наименьших квадратов не предполагает нормально распределенных ошибок при вычислении оценок параметров, метод лучше всего работает для данных, которые не содержат большого количества случайных ошибок с экстремальными значениями. Нормальное распределение - это одно из вероятностных распределений, в которых экстремальные случайные ошибки встречаются редко. Однако статистические результаты, такие как пределы достоверности и прогнозирования, действительно требуют обычно распределенных ошибок для их достоверности.

Если среднее значение ошибок равно нулю, то ошибки являются чисто случайными. Если среднее значение не равно нулю, то может оказаться, что модель не является правильным выбором для ваших данных, или ошибки не являются чисто случайными и содержат систематические ошибки.

Постоянная дисперсия в данных подразумевает, что «разброс» ошибок постоянен. Иногда говорят, что данные с одинаковой дисперсией имеют одинаковое качество.

Предположение о том, что случайные ошибки имеют постоянную дисперсию, не является неявным для взвешенной регрессии наименьших квадратов. Вместо этого предполагается, что веса, предусмотренные в процедуре подгонки, правильно указывают различные уровни качества, присутствующие в данных. Затем веса используются для регулировки величины влияния каждой точки данных на оценки установленных коэффициентов до соответствующего уровня.

Линейные наименьшие квадраты

Программное обеспечение панели инструментов фитинга кривой использует метод линейных наименьших квадратов для подгонки линейной модели к данным. Линейная модель определяется как уравнение, которое является линейным в коэффициентах. Например, полиномы являются линейными, но гауссовы - нет. Чтобы проиллюстрировать линейный процесс подгонки методом наименьших квадратов, предположим, что у вас есть n точек данных, которые могут быть смоделированы полиномом первой степени.

$y =_{} {p1x}_{}$ + p2

Чтобы решить это уравнение для неизвестных коэффициентов p1 и p2, запишите S как систему n одновременных линейных уравнений в двух неизвестных. Если n больше числа неизвестных, то система уравнений переопределяется.

$_{}^{S=∑i=1n} {(_{} yi -_{} (_{}_{p1xi} +}^{}$ p2)) 2

Поскольку процесс подгонки методом наименьших квадратов сводит к минимуму суммированный квадрат остатков, коэффициенты определяются путем дифференцирования S относительно каждого параметра и установки результата равным нулю.

$\begin{array}{l} \frac{}{_{}}_{}^{}_{∂S∂p1=−2∑i=1nxi} (_{} yi -_{} (_{}_{p1xi} + \\ \frac{p2)}{)_{}}_{}^{}_{} {=0∂S∂p2=−2∑i=1n}_{} (_{} yi_{−} ( \end{array}$ p1xi + p2)) = 0

Оценки истинных параметров обычно представлены как b. Заменяя b1 и b2 на p1 и p2, предыдущие уравнения становятся

$\begin{matrix} _{∑xi} (_{} yi -_{} (_{}_{b1xi} + \\ b2 ) ) = 0_{} \sum (_{} {yi}_{} -_{(} b1xi \end{matrix}$ + b2)) = 0

где суммирование выполняется от i = 1 до n. Нормальные уравнения определяются как

$\begin{matrix} _{}_{}^{}_{}_{}_{}_{} \\ _{}_{}_{}_{b1∑xi2+b2∑xi=∑xiyib1∑xi+nb2=∑yi} \end{matrix}$

Решение для b1

$_{} \frac{_{}_{}_{}_{}}{_{}^{} b1=n\sumxiyi-\sumxi\sumyin\sumxi2- {(_{} \sumxi}^{)}}$ 2

Решение для b2 с использованием значения b1

$_{b2} \frac{=}{} 1n_{(}_{}_{}$ ∑yi−b1∑xi)

Как видно, оценка коэффициентов p1 и p2 требует лишь нескольких простых вычислений. Распространение этого примера на многочлен более высокой степени является простым, хотя и немного утомительным. Все, что требуется, это дополнительное нормальное уравнение для каждого линейного члена, добавленного в модель.

В матричном виде линейные модели задаются формулой

y = Xβ +

где

y - вектор ответов n-на-1.
β - вектор коэффициентов m-by-1.
X - матрица конструкции n-by-m для модели.
λ - вектор ошибок n-by-1.

Для многочлена первой степени n уравнений в двух неизвестных выражаются в терминах y, X и β как

$[\begin{matrix} _{} \\ _{} \\ _{y1y2y3} \\ . \\ . \\ . \\ _{} \end{matrix} yn] \begin{matrix} =_{} [ \\ _{} \\ _{} \\ x11x21x31 \\ ._{.} . \end{matrix} \begin{array}{l} {xn1}_{]} \\ _{×} \end{array}$ [p1p2]

Решением задачи с наименьшими квадратами является вектор b, который оценивает неизвестный вектор коэффициентов β. Нормальные уравнения задаются

(^XTX) b = ^XTy

где ^XT - транспонирование матрицы дизайна X. Решение для b,

b = (^XTX) ^-1 ^XTy

Используйте оператор обратной косой черты MATLAB ® (mldivide) для решения системы одновременных линейных уравнений для неизвестных коэффициентов. Поскольку инвертирование ^XTX может привести к недопустимым ошибкам округления, оператор обратной косой черты использует QR разложение с поворотом, что является очень стабильным алгоритмом численно. Дополнительные сведения об операторе обратной косой черты и декомпозиции QR см. в разделе Арифметические операции.

Можно снова подключить b к формуле модели, чтобы получить прогнозируемые значения отклика, ŷ.

ŷ = Xb = Hy

H = X (^XTX⁾ -1 XT

Шляпа (циркумфлекс) над буквой обозначает оценку параметра или предсказание из модели. Проекционная матрица H называется матрицей шляпы, потому что она ставит шляпу на y.

Остатки задаются

r = y - ŷ = (1-H) y

Взвешенные наименьшие квадраты

Обычно предполагается, что данные ответа имеют одинаковое качество и, следовательно, имеют постоянную дисперсию. Если это предположение нарушено, на вашу подгонку могут оказать чрезмерное влияние данные низкого качества. Для улучшения подгонки можно использовать взвешенную регрессию наименьших квадратов, когда в процесс подгонки включается дополнительный масштабный коэффициент (вес). Взвешенная регрессия методом наименьших квадратов минимизирует оценку ошибки

$_{}^{}_{s=∑i=1nwi} {(_{} yi {\bar{}}_{} y}^{}$ ^ i) 2

где _wi - веса. Веса определяют, насколько каждое значение отклика влияет на окончательные оценки параметров. Точка данных высокого качества влияет на посадку больше, чем точка данных низкого качества. Взвешивание данных рекомендуется в том случае, если веса известны или если существует обоснование того, что они соответствуют определенной форме.

Веса изменяют выражение для оценок параметров b следующим образом:

$b \overset{}{=} β {^^{} = (}^{}^{XTWX})$ − 1XTWy

где W задается диагональными элементами весовой матрицы w.

Часто можно определить, не являются ли отклонения постоянными, подгоняя данные и выводя на печать остатки. На графике, показанном ниже, данные содержат реплицированные данные различного качества, и предполагается, что аппроксимация верна. Данные низкого качества обнаруживаются на графике остатков, который имеет форму «воронки», где малые значения предиктора дают больший разброс в значениях ответа, чем большие значения предиктора.

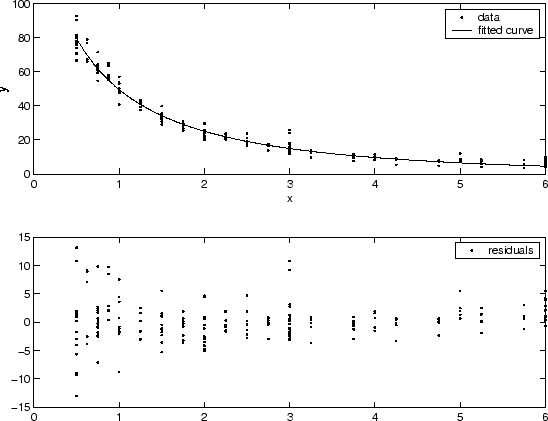
Вводимые веса должны преобразовывать отклонения отклика в постоянное значение. Если известны отклонения ошибок измерения в данных, то веса задаются

$_{wi} =_{}^{}$ 1/starti2

Или, если имеются только оценки переменной ошибки для каждой точки данных, обычно достаточно использовать эти оценки вместо истинной дисперсии. Если отклонения неизвестны, достаточно указать веса в относительном масштабе. Следует отметить, что общий срок отклонения оценивается даже в том случае, если были определены веса. В этом случае веса определяют относительный вес каждой точки посадки, но не используются для указания точной дисперсии каждой точки.

Например, если каждая точка данных является средним значением нескольких независимых измерений, может быть целесообразно использовать эти числа измерений в качестве весов.

Надежные наименьшие квадраты

Обычно предполагается, что ошибки ответа следуют за нормальным распределением и что экстремальные значения редки. Тем не менее, экстремальные значения, называемые отклонениями, действительно имеют место.

Основным недостатком фитинга с наименьшими квадратами является его чувствительность к отклонениям. Отклонения оказывают большое влияние на аппроксимацию, поскольку возведение остатков в квадрат увеличивает влияние этих крайних точек данных. Чтобы минимизировать влияние отклонений, можно подогнать данные с помощью надежной регрессии методом наименьших квадратов. Панель инструментов предоставляет следующие два надежных метода регрессии:

Наименьшие абсолютные остатки (LAR) - метод LAR находит кривую, которая минимизирует абсолютную разность остатков, а не квадратичные разности. Поэтому экстремальные значения оказывают меньшее влияние на прилегание.
Весы Bisquare - этот метод минимизирует взвешенную сумму квадратов, где вес каждой точки данных зависит от того, как далеко точка находится от подгоняемой линии. Очки возле линии получают полный вес. Очки дальше от линии получают уменьшенный вес. Очки, которые находятся дальше от линии, чем можно было бы ожидать по случайной случайности, получают нулевой вес.
Для большинства случаев метод веса бисквара предпочтительнее, чем LAR, потому что он одновременно стремится найти кривую, которая соответствует большей части данных, используя обычный подход наименьших квадратов, и он минимизирует эффект отклонений.

Надежная подгонка с весами bisquare использует итерационно перезаряженный алгоритм наименьших квадратов и выполняет следующую процедуру:

Подгонка модели по взвешенным наименьшим квадратам.
Вычислите скорректированные остатки и стандартизируйте их. Скорректированные остатки даны
$_{radj} \frac{=_{}}{\sqrt{{ri1}_{}}}$ − hi
_ri являются обычными остатками наименьших квадратов, а _hi - рычагами, которые регулируют остатки, уменьшая вес высокоэффективных точек данных, которые оказывают большое влияние на подгонку наименьших квадратов. Стандартизированные скорректированные остатки даны
$u \frac{=_{}}{}$ radjKs
K - постоянная настройки, равная 4,685, и s - надежное стандартное отклонение, заданное MAD/0.6745, где MAD - среднее абсолютное отклонение остатков.
Вычислите надежные веса как функцию u. Веса bisquare даны как
$_{wi} = \begin{matrix} {({1_{-}}^{(}^{ui} & )_{2}) \\ _{} \end{matrix}$ 2|ui|<10|ui|≥1
Обратите внимание, что при вводе собственного вектора регрессионного веса конечный вес является произведением надежного веса и регрессионного веса.
Если посадка сходится, то вы закончите. В противном случае выполните следующую итерацию процедуры фитинга, вернувшись к первому шагу.

График, показанный ниже, сравнивает обычную линейную посадку с устойчивой посадкой с использованием весов бисквара. Обратите внимание, что надежная посадка следует за большей частью данных и не подвергается сильному влиянию отклонений.

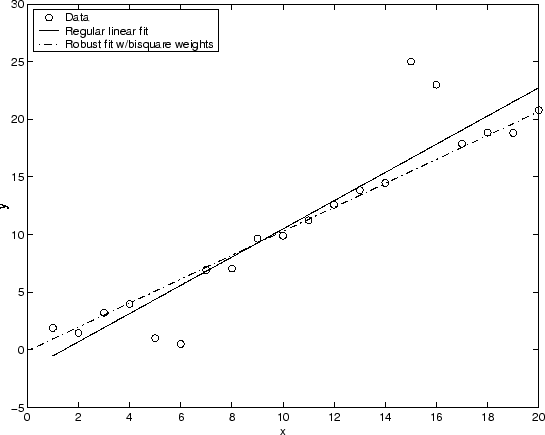
Вместо минимизации влияния отклонений с помощью надежной регрессии можно отметить точки данных, которые будут исключены из аппроксимации. Дополнительные сведения см. в разделе Удаление отклонений.

Нелинейные наименьшие квадраты

Программное обеспечение панели инструментов фитинга кривой использует нелинейную формулировку наименьших квадратов для подгонки нелинейной модели к данным. Нелинейная модель определяется как уравнение, которое является нелинейным в коэффициентах, или как комбинация линейного и нелинейного в коэффициентах. Например, гауссовы, отношения многочленов и степенные функции являются нелинейными.

В матричном виде нелинейные модели задаются формулой

y = f (X, β) +

где

y - вектор ответов n-на-1.
f - функция β и X.
β - вектор коэффициентов m-by-1.
X - матрица конструкции n-by-m для модели.
λ - вектор ошибок n-by-1.

Нелинейные модели труднее подгонять, чем линейные, поскольку коэффициенты нельзя оценить с помощью простых матричных методов. Вместо этого требуется итеративный подход, который следует следующим шагам:

Начните с начальной оценки для каждого коэффициента. Для некоторых нелинейных моделей предусмотрен эвристический подход, который дает разумные начальные значения. Для других моделей предоставляются случайные значения на интервале [0,1].
Создайте подгоняемую кривую для текущего набора коэффициентов. Аппроксимированное значение отклика ŷ задается
ŷ = f (X, b)
и включает вычисление якобиана f (X, b), который определяется как матрица частных производных, взятых относительно коэффициентов.
Отрегулируйте коэффициенты и определите, улучшится ли посадка. Направление и величина регулировки зависят от алгоритма подгонки. Панель инструментов предоставляет следующие алгоритмы:
- Область доверия - это алгоритм по умолчанию, который должен использоваться, если заданы ограничения коэффициентов. Он может решать сложные нелинейные задачи более эффективно, чем другие алгоритмы, и представляет собой улучшение по сравнению с популярным алгоритмом Левенберга-Марквардта.
- Левенберг-Марквардт (Levenberg-Marquardt) - этот алгоритм используется в течение многих лет и доказал, что он работает большую часть времени для широкого диапазона нелинейных моделей и стартовых значений. Если алгоритм доверительной области не дает разумного соответствия и у вас нет ограничений коэффициентов, следует попробовать алгоритм Левенберга-Марквардта.
Выполните итерацию процесса, возвращаясь к шагу 2, пока аппроксимация не достигнет заданных критериев сходимости.

Для нелинейных моделей можно использовать веса и надежный фитинг, и процесс фитинга изменяется соответствующим образом.

Из-за характера процесса аппроксимации ни один алгоритм не является безупречным для всех нелинейных моделей, наборов данных и начальных точек. Поэтому, если с помощью исходных точек, алгоритма и критериев сходимости по умолчанию не удается достичь разумного соответствия, следует поэкспериментировать с различными опциями. Описание изменения параметров по умолчанию см. в разделе Определение параметров посадки и оптимизированные начальные точки. Поскольку нелинейные модели могут быть особенно чувствительны к начальным точкам, это должен быть первый вариант вписывания, который вы изменяете.

Прочный фитинг

Открыть сценарий в реальном времени

В этом примере показано, как сравнить эффекты исключения отклонений и надежной подгонки. В примере показано, как исключить отклонения на произвольном расстоянии, превышающем 1,5 стандартных отклонения от модели. Затем эти шаги сравнивают удаление отклонений с заданием надежной посадки, которая дает меньший вес отклонениям.

Создайте синусоидальный сигнал базовой линии:

xdata = (0:0.1:2*pi)'; 
y0 = sin(xdata);

Добавьте шум к сигналу с непостоянной дисперсией.

% Response-dependent Gaussian noise
gnoise = y0.*randn(size(y0));

% Salt-and-pepper noise
spnoise = zeros(size(y0)); 
p = randperm(length(y0));
sppoints = p(1:round(length(p)/5));
spnoise(sppoints) = 5*sign(y0(sppoints));

ydata = y0 + gnoise + spnoise;

Поместите шумные данные в синусоидальную модель базовой линии и укажите 3 выходных аргумента для получения информации о подгонке, включая остатки.

f = fittype('a*sin(b*x)'); 
[fit1,gof,fitinfo] = fit(xdata,ydata,f,'StartPoint',[1 1]);

Проверьте информацию в структуре фитинфо.

fitinfo

fitinfo = struct with fields:
           numobs: 63
         numparam: 2
        residuals: [63x1 double]
         Jacobian: [63x2 double]
         exitflag: 3
    firstorderopt: 0.0883
       iterations: 5
        funcCount: 18
     cgiterations: 0
        algorithm: 'trust-region-reflective'
         stepsize: 4.1539e-04
          message: 'Success, but fitting stopped because change in residuals less than tolerance (TolFun).'

Извлеките остатки из структуры фитинфо.

residuals = fitinfo.residuals;

Определите «отклонения» как точки на произвольном расстоянии, превышающем 1,5 стандартных отклонения от базовой модели, и измените данные, исключив отклонения.

I = abs( residuals) > 1.5 * std( residuals );
outliers = excludedata(xdata,ydata,'indices',I);

fit2 = fit(xdata,ydata,f,'StartPoint',[1 1],...
           'Exclude',outliers);

Сравните эффект исключения отклонений с эффектом придания им более низкого веса бисквара при надежной посадке.

fit3 = fit(xdata,ydata,f,'StartPoint',[1 1],'Robust','on');

Постройте график данных, отклонений и результатов посадок. Укажите информативную легенду.

plot(fit1,'r-',xdata,ydata,'k.',outliers,'m*') 
hold on
plot(fit2,'c--')
plot(fit3,'b:')
xlim([0 2*pi])
legend( 'Data', 'Data excluded from second fit', 'Original fit',...
    'Fit with points excluded', 'Robust fit' )
hold off

Figure contains an axes. The axes contains 5 objects of type line. These objects represent Data, Data excluded from second fit, Original fit, Fit with points excluded, Robust fit.

Постройте график остатков для двух посадок с учетом отклонений:

figure 
plot(fit2,xdata,ydata,'co','residuals') 
hold on
plot(fit3,xdata,ydata,'bx','residuals')
hold off

Figure contains an axes. The axes contains 4 objects of type line. These objects represent data, zero line.

Документация