Параметрический фитинг включает в себя поиск коэффициентов (параметров) для одной или нескольких моделей, которые соответствуют данным. Предполагается, что данные носят статистический характер и подразделяются на два компонента:
данные = детерминированная составляющая + случайная составляющая
Детерминированный компонент задается параметрической моделью, и случайный компонент часто описывается как ошибка, связанная с данными:
data = параметрическая модель + ошибка
Модель является функцией независимой (предикторной) переменной и одного или нескольких коэффициентов. Ошибка представляет случайные изменения в данных, которые следуют за определенным распределением вероятностей (обычно гауссовым). Вариации могут быть получены из различных источников, но всегда присутствуют на определенном уровне при работе с измеренными данными. Систематические вариации также могут существовать, но они могут привести к подобранной модели, которая плохо представляет данные.
Коэффициенты модели часто имеют физическое значение. Например, предположим, что вы собрали данные, которые соответствуют одному режиму распада радиоактивного нуклида, и хотите оценить период полураспада (T1/2) распада. Закон радиоактивного распада гласит, что активность радиоактивного вещества распадается во времени экспоненциально. Поэтому модель, которая будет использоваться при посадке, задается
− λ t
где y0 - число ядер в момент времени t = 0, а λ - постоянная распада. Данные могут быть описаны
ошибка
И y0, и λ - коэффициенты, которые оцениваются по аппроксимации. Поскольку T1/2 = ln (2 )/λ, аппроксимированное значение константы распада дает аппроксимированный период полураспада. Однако, поскольку данные содержат некоторую ошибку, детерминированная составляющая уравнения не может быть определена точно из данных. Поэтому коэффициенты и расчет периода полураспада будут иметь некоторую неопределенность, связанную с ними. Если неопределенность допустима, выполняется подбор данных. Если неопределенность неприемлема, то, возможно, придется предпринять шаги для ее уменьшения либо путем сбора большего количества данных, либо путем уменьшения погрешности измерений, сбора новых данных и повторения подгонки модели.
При других проблемах, когда нет теории диктовать модель, можно также изменить модель путем добавления или удаления терминов или заменить совершенно другую модель.
Модели параметрической библиотеки «Фитинг кривой» (Curve Fitting) Toolbox™ описаны в следующих разделах.
Выберите тип модели для подгонки в раскрывающемся списке приложения «Фитинг кривой».
Какие типы посадок можно использовать для кривых или поверхностей? На основе выбранных данных в списке категорий подгонки отображаются категории кривых или поверхностей. В следующей таблице описаны опции кривых и поверхностей.
| Вписать категорию | Кривые | Поверхности |
|---|---|---|
| Регрессионные модели | ||
| Полиномиал | Да (до степени 9) | Да (до степени 5) |
| Показательный | Да | |
| Фурье | Да | |
| Гауссовский | Да | |
| Власть | Да | |
| Рациональный | Да | |
| Сумма синусов | Да | |
| Weibull | Да | |
| Интерполяция | ||
| Interpolant | Да Методы: Ближайший сосед Линейный Кубический Сохранение формы (PCHIP) | Да Методы: Ближайший сосед Линейный Кубический Biharmonic Тонколистовой шлиц |
| Сглаживание | ||
| Сглаживание сплайна | Да | |
| Lowess | Да | |
| Обычай | ||
| Пользовательское уравнение | Да | Да |
| Пользовательский линейный фитинг | Да | |
Для всех категорий соответствия просмотрите на панели Результаты (Results) термины модели, значения коэффициентов и статистику соответствия.
Совет
При возникновении проблем с посадкой сообщения на панели Результаты (Results) помогают определить лучшие настройки.
Приложение «Фитинг кривой» предоставляет набор типов и параметров подгонки, которые можно изменить для улучшения подгонки. Сначала попробуйте использовать значения по умолчанию, а затем поэкспериментируйте с другими параметрами.
Общие сведения об использовании доступных опций подгонки см. в разделах Определение опций подгонки и Оптимизированные начальные точки.
Можно попробовать различные настройки в пределах одной фигуры посадки, а также создать несколько посадок для сравнения. При создании нескольких посадок можно сравнивать различные типы посадок и настройки рядом в приложении «Фитинг кривой». См. раздел Создание нескольких посадок в приложении «Фитинг кривой».
Имя модели библиотеки можно указать как строку при вызове fit функция. Например, для задания квадратичного poly2:
f = fit( x, y, 'poly2' )
См. раздел Список библиотечных моделей для фитинга кривой и поверхности (List of Library Models for Curve and Surface Fitting), чтобы просмотреть все доступные имена библиотечных моделей.
Вы также можете использовать fittype для построения функции fittype для библиотечной модели и используйте fittype в качестве входных данных для fit функция.
Используйте fitoptions чтобы узнать, какие параметры можно задать, например:
fitoptions(poly2)
Примеры см. в разделах для каждого типа модели, перечисленных в таблице в разделе Интерактивный выбор типа модели. Дополнительные сведения обо всех функциях создания и анализа моделей см. в разделе Фитинг кривой и поверхности.
Для большинства типов моделей в приложении «Фитинг кривой» используется опция «Центр и масштаб». При выборе этого параметра инструмент корректируется с учетом центрированных и масштабированных данных, применяя Normalize установка переменных. В командной строке можно использовать Normalize в качестве входного аргумента для fitoptions функция. См. раздел fitoptions справочная страница.
Как правило, это хорошая идея для нормализации входных данных (также известных как данные предиктора), которые могут облегчить численные проблемы с переменными различных масштабов. Например, предположим, что входными данными подгонки поверхности являются частота вращения двигателя с диапазоном 500-4500 r/мин и процент нагрузки двигателя с диапазоном 0-1. Затем, Центр (Center) и Масштаб (Scale), как правило, улучшают подгонку из-за большой разницы в масштабе между двумя входами. Однако если входные данные находятся в одних и тех же единицах или в аналогичном масштабе (например, на востоке и севере для географических данных), то центр и масштаб менее полезны. При нормализации входных данных с помощью этой опции значения соответствующих коэффициентов изменяются по сравнению с исходными данными.
Если выполняется подгонка кривой или поверхности для оценки коэффициентов или коэффициенты имеют физическую значимость, снимите флажок Центр и масштаб (Center and scale). На графиках приложения «Фитинг кривой» используется исходный масштаб с опцией «Центр и масштаб» или без нее.
В командной строке, чтобы задать параметр для центрирования и масштабирования данных перед подгонкой, создайте структуру параметров подгонки по умолчанию, задайте Normalize кому on, затем совместим с опциями:
options = fitoptions;
options.Normal = 'on';
options
options =
Normalize: 'on'
Exclude: [1x0 double]
Weights: [1x0 double]
Method: 'None'
load census
f1 = fit(cdate,pop,'poly3',options)Опции интерактивного вписывания описаны в следующих разделах. Сведения о программном задании тех же параметров подгонки см. в разделе Задание параметров подгонки в командной строке.
Чтобы в интерактивном режиме задать опции подгонки в приложении «Фитинг кривой», нажмите кнопку «Параметры подгонки», чтобы открыть диалоговое окно «Параметры подгонки». Все категории подгонки, кроме интерполяторов и сглаживающих сплайнов, имеют конфигурируемые опции подгонки.
Доступные опции зависят от того, подгоняются ли данные с помощью линейной модели, нелинейной модели или непараметрического типа посадки:
Все опции, описанные ниже, доступны для нелинейных моделей.
Ограничения нижнего и верхнего коэффициентов являются единственными опциями подгонки, доступными в диалоговом окне для линейных моделей полиномов. Для полиномов можно задать значение «Надежный» в приложении «Фитинг кривой», не открывая диалоговое окно «Параметры подгонки».
Непараметрические типы подгонки не имеют дополнительных опций подгонки (интерполяция, сглаживание сплайна и снижение).
Варианты подгонки для одномерной экспоненты показаны ниже. Начальные значения коэффициентов и ограничения относятся к данным переписи.
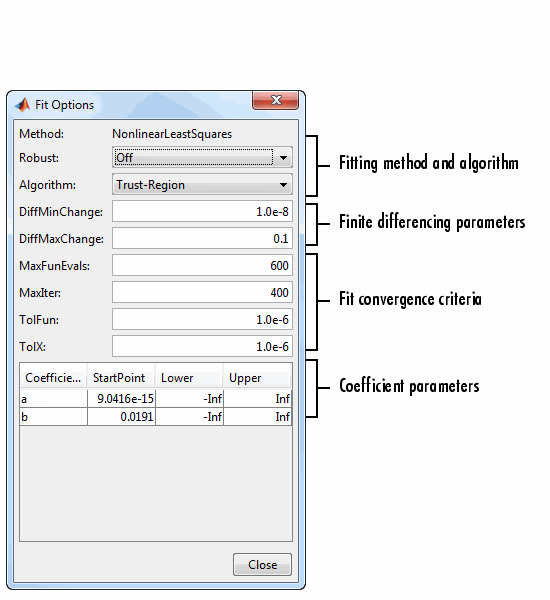
Метод - метод подгонки.
Метод выбирается автоматически на основе используемой библиотеки или пользовательской модели. Для линейных моделей используется метод LinearSquares. Для нелинейных моделей используется метод Нелинейные квадраты.
Надежный (Rustive) - указывает, следует ли использовать метод надежного фитинга методом наименьших квадратов.
Откл (Off) - не использовать надежный фитинг (по умолчанию).
Вкл. (On) - вписывается с помощью надежного метода по умолчанию (весы bisquare).
LAR - подгонка путем минимизации наименьших абсолютных остатков (LAR).
Bisquare - подгонка путем минимизации суммированного квадрата остатков и уменьшения веса отклонений с помощью весов bisquare. В большинстве случаев это лучший выбор для надежной установки.
Алгоритм - алгоритм, используемый для процедуры подгонки:
Область доверия - это алгоритм по умолчанию, который должен использоваться, если заданы ограничения нижнего или верхнего коэффициентов.
Левенберг-Марквардт (Levenberg-Marquardt) - если алгоритм доверительной области не дает разумного соответствия и у вас нет ограничений коэффициентов, попробуйте алгоритм Левенберга-Марквардта.
DiffMinChange - минимальное изменение коэффициентов для конечной разницы якобинцев. Значение по умолчанию - 10-8.
DiffMaxChange - максимальное изменение коэффициентов для конечных разностей якобианцев. Значение по умолчанию - 0,1.
Обратите внимание, что DiffMinChange и DiffMaxChange применяются к:
Любое нелинейное пользовательское уравнение, то есть нелинейное уравнение, которое вы пишете
Некоторые нелинейные уравнения, поставляемые с программным обеспечением панели инструментов фитинга кривой
Однако DiffMinChange и DiffMaxChange не применяются ни к каким линейным уравнениям.
MaxFunEvals - максимально допустимое количество оценок функций (модели). Значение по умолчанию - 600.
MaxIter - максимально допустимое количество итераций подгонки. Значение по умолчанию - 400.
TolFun - допуск окончания, используемый для условий остановки, включающих значение функции (модели). Значение по умолчанию - 10-6.
TolX - допуск окончания, используемый в условиях остановки с использованием коэффициентов. Значение по умолчанию - 10-6.
Коэффициенты - символы для неизвестных коэффициентов, которые должны быть установлены.
StartPoint - начальные значения коэффициентов. Значения по умолчанию зависят от модели. Для рациональных, Вейбулла и пользовательских моделей значения по умолчанию выбираются случайным образом в диапазоне [0,1]. Для всех других нелинейных библиотечных моделей начальные значения зависят от набора данных и вычисляются эвристически. См. оптимизированные начальные точки ниже.
Нижний (Lower) - нижние границы установленных коэффициентов. Инструмент использует только границы с алгоритмом подгонки области доверия. Нижние границы по умолчанию для большинства библиотечных моделей: -Inf, что указывает на то, что коэффициенты не ограничены. Однако некоторые модели имеют конечные нижние границы по умолчанию. Например, для гауссов параметр width ограничен так, что он не может быть меньше 0. См. ограничения по умолчанию ниже.
Верхний - верхние границы на соответствующих коэффициентах. Инструмент использует только границы с алгоритмом подгонки области доверия. Верхними границами по умолчанию для всех библиотечных моделей являются Inf, что указывает на то, что коэффициенты не ограничены.
Дополнительные сведения об этих опциях подгонки см. в разделе lsqcurvefit в документации по Toolbox™ оптимизации.
Начальные точки коэффициентов по умолчанию и ограничения для библиотечных и пользовательских моделей показаны в следующей таблице. Если начальные точки оптимизированы, то они вычисляются эвристически на основе текущего набора данных. Случайные начальные точки определяются на интервале [0,1], и линейные модели не требуют начальных точек.
Если модель не имеет ограничений, коэффициенты не имеют ни нижней, ни верхней границы. Можно переопределить начальные точки и ограничения по умолчанию, указав собственные значения в диалоговом окне Опции вписывания (Fit Options).
Начальные точки и ограничения по умолчанию
Модель | Начальные точки | Ограничения |
|---|---|---|
Пользовательский линейный | Н/Д | Ничего |
Нелинейный пользовательский | Случайный | Ничего |
Показательный | Оптимизированный | Ничего |
Фурье | Оптимизированный | Ничего |
Гауссовский | Оптимизированный | ci > 0 |
Полиномиал | Н/Д | Ничего |
Власть | Оптимизированный | Ничего |
Рациональный | Случайный | Ничего |
Сумма синусов | Оптимизированный | bi > 0 |
Weibull | Случайный | a, b > 0 |
Следует отметить, что сумма синусов и модели рядов Фурье особенно чувствительны к начальным точкам, и оптимизированные значения могут быть точными только для нескольких членов в связанных уравнениях.
Создайте структуру опций вписывания по умолчанию и задайте параметр для центрирования и масштабирования данных перед подгонкой:
options = fitoptions;
options.Normal = 'on';
options
options =
Normalize: 'on'
Exclude: [1x0 double]
Weights: [1x0 double]
Method: 'None'Изменение структуры опций вписывания по умолчанию полезно, если необходимо задать Normalize, Exclude, или Weights и затем подгонять данные с помощью одних и тех же опций с различными методами подгонки. Например:
load census f1 = fit(cdate,pop,'poly3',options); f2 = fit(cdate,pop,'exp1',options); f3 = fit(cdate,pop,'cubicsp',options);
Зависящие от данных параметры аппроксимации возвращаются в третьем выходном аргументе fit функция. Например, параметр сглаживания для сглаживания сплайна зависит от данных:
[f,gof,out] = fit(cdate,pop,'smooth');
smoothparam = out.p
smoothparam =
0.0089Используйте опции вписывания для изменения параметра сглаживания по умолчанию для нового вписывания:
options = fitoptions('Method','Smooth','SmoothingParam',0.0098);
[f,gof,out] = fit(cdate,pop,'smooth',options);Дополнительные сведения об использовании параметров посадки см. в разделе fitoptions справочная страница.