Документация

Набор данных SIN

Первый набор эталонных данных представляет собой простую задачу аппроксимации функции. Сеть 1-5-1, с tansig передаточные функции в скрытом слое и линейная передаточная функция в выходном слое используются для аппроксимации одного периода синусоидальной волны. В следующей таблице приведены результаты обучения сети с использованием девяти различных алгоритмов обучения. Каждая запись в таблице представляет 30 различных испытаний, где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучают до тех пор, пока квадрат ошибки не станет меньше 0,002. Самый быстрый алгоритм для этой задачи - алгоритм Левенберга - Марквардта. В среднем он в четыре раза быстрее следующего самого быстрого алгоритма. Это тип задачи, для которой лучше всего подходит алгоритм LM - задача аппроксимации функции, где сеть имеет меньше ста весов и аппроксимация должна быть очень точной.

На производительность различных алгоритмов может влиять точность, требуемая для аппроксимации. Это показано на следующем рисунке, который отображает среднюю квадратную ошибку в зависимости от времени выполнения (усредненное за 30 испытаний) для нескольких репрезентативных алгоритмов. Здесь видно, что ошибка в алгоритме LM со временем уменьшается гораздо быстрее, чем другие показанные алгоритмы.

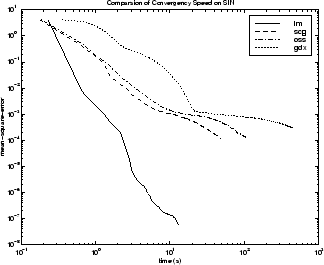
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. Здесь видно, что по мере уменьшения цели ошибки улучшение, обеспечиваемое алгоритмом LM, становится более выраженным. Некоторые алгоритмы работают лучше по мере уменьшения цели ошибки (LM и BFG), а другие алгоритмы ухудшаются по мере уменьшения цели ошибки (OSS и GDX).

Набор данных ЧЕТНОСТИ

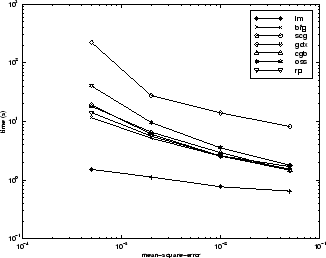
Второй проблемой эталонного теста является простая проблема распознавания образов - обнаружение четности 3-битного числа. Если количество единиц во входном шаблоне нечетное, то сеть должна выводить 1; в противном случае он должен выводить -1. Сеть, используемая для этой проблемы, представляет собой сеть 3-10-10-1 с нейронами тансиг в каждом слое. В следующей таблице приведены результаты обучения этой сети с использованием девяти различных алгоритмов. Каждая запись в таблице представляет 30 различных испытаний, где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучается до тех пор, пока квадрат ошибки не станет меньше 0,001. Самый быстрый алгоритм для этой проблемы - алгоритм упругого обратного распространения, хотя алгоритмы сопряженного градиента (в частности, алгоритм масштабированного сопряженного градиента) почти такие же быстрые. Обратите внимание, что алгоритм LM не справляется с этой проблемой. В общем, алгоритм LM не так хорошо работает с проблемами распознавания образов, как с проблемами аппроксимации функций. Алгоритм LM предназначен для задач наименьших квадратов, которые являются приблизительно линейными. Поскольку выходные нейроны в проблемах распознавания образов, как правило, насыщены, вы не будете работать в линейной области.

Как и в случае проблем аппроксимации функций, на производительность различных алгоритмов может влиять точность, требуемая сетью. Это показано на следующем рисунке, на котором показана среднеквадратическая ошибка в зависимости от времени выполнения для некоторых типичных алгоритмов. Алгоритм LM быстро сходится после некоторого момента, но только после того, как другие алгоритмы уже сошлись.

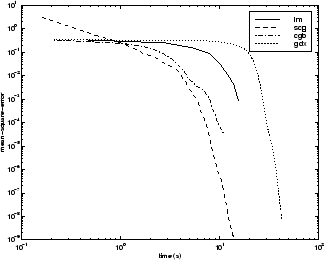
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. Снова видно, что некоторые алгоритмы ухудшаются по мере уменьшения цели ошибки (OSS и BFG).

Набор данных ENGINE

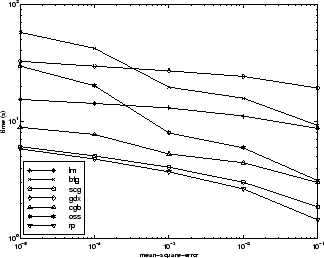
Третья задача эталона - это задача аппроксимации реалистичной функции (или нелинейной регрессии). Данные получают из работы двигателя. Входами в сеть являются частота вращения двигателя и уровни заправки, а выходами сети - крутящий момент и уровни выбросов. Сеть, используемая для этой проблемы, представляет собой сеть 2-30-2 с нейронами тансиг в скрытом слое и линейными нейронами в выходном слое. В следующей таблице приведены результаты обучения этой сети с использованием девяти различных алгоритмов. Каждая запись в таблице представляет 30 различных испытаний (10 испытаний для RP и GDX из-за временных ограничений), где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучают до тех пор, пока квадрат ошибки не станет меньше 0,005. Самым быстрым алгоритмом для этой задачи является алгоритм LM, за которым следуют алгоритм квази-Ньютона BFGS и алгоритмы сопряженного градиента. Хотя это проблема аппроксимации функции, алгоритм LM не так явно превосходит, как это было в наборе данных SIN. В этом случае количество весов и смещений в сети значительно больше, чем используемое в проблеме SIN (152 против 16), и преимущества алгоритма LM уменьшаются по мере увеличения числа параметров сети.

На следующем рисунке показана среднеквадратическая ошибка в зависимости от времени выполнения для некоторых типичных алгоритмов. Производительность алгоритма LM улучшается с течением времени по сравнению с другими алгоритмами.

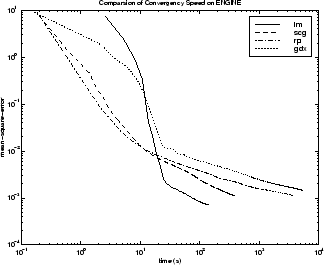
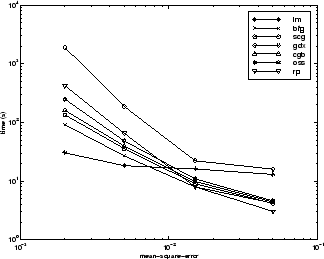
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. Снова видно, что некоторые алгоритмы ухудшаются по мере уменьшения цели ошибки (GDX и RP), в то время как алгоритм LM улучшается.

Набор данных CANCER

Четвертая задача эталона - это задача реалистичного распознавания образов (или нелинейного дискриминантного анализа). Целью сети является классификация опухоли как доброкачественной или злокачественной на основе описаний клеток, собранных при микроскопическом исследовании. Входные атрибуты включают толщину комка, однородность размера и формы ячейки, величину предельной адгезии и частоту голых ядер. Данные были получены из больниц Университета Висконсина, Мэдисон, от доктора Уильяма Х. Вольберга. Сеть, используемая для этой проблемы, представляет собой сеть 9-5-5-2 с нейронами тансиг во всех слоях. В следующей таблице приведены результаты обучения этой сети с использованием девяти различных алгоритмов. Каждая запись в таблице представляет 30 различных испытаний, где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучается до тех пор, пока квадрат ошибки не станет меньше 0,012. Несколько прогонов не смогли сойтись для некоторых алгоритмов, поэтому для получения статистики использовались только верхние 75% прогонов из каждого алгоритма.

Сопряженные алгоритмы градиента и упругое обратное распространение обеспечивают быструю сходимость, и алгоритм LM также является достаточно быстрым. Как и в случае набора данных четности, алгоритм LM не работает так же хорошо над проблемами распознавания образов, как и над проблемами аппроксимации функций.

На следующем рисунке показана среднеквадратическая ошибка в зависимости от времени выполнения для некоторых типичных алгоритмов. Для этой проблемы существует не так много изменений в производительности, как в предыдущих проблемах.

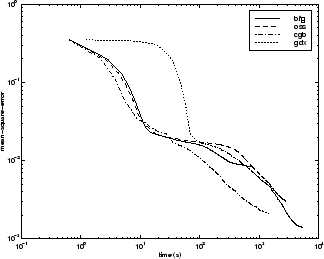
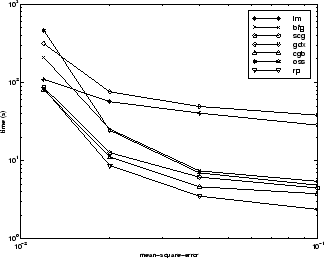
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. Снова видно, что некоторые алгоритмы ухудшаются по мере уменьшения цели ошибки (OSS и BFG), в то время как алгоритм LM улучшается. Типично для алгоритма LM при любой проблеме, что его производительность улучшается по сравнению с другими алгоритмами по мере уменьшения цели ошибки.

НАБОР ДАННЫХ ПО ХОЛЕСТЕРИНУ

Пятая задача эталона - это задача аппроксимации реалистичной функции (или нелинейной регрессии). Целью сети является прогнозирование уровней холестерина (ldl, hdl и vldl) на основе измерений 21 спектрального компонента. Данные были получены от доктора Нила Пурди, химического факультета, Университет штата Оклахома [PuLu92]. Сеть, используемая для этой проблемы, представляет собой сеть 21-15-3 с нейронами тансиг в скрытых слоях и линейными нейронами в выходном слое. В следующей таблице приведены результаты обучения этой сети с использованием девяти различных алгоритмов. Каждая запись в таблице представляет 20 различных испытаний (10 испытаний для RP и GDX), где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучается до тех пор, пока квадрат ошибки не станет меньше 0,027.

Масштабируемый алгоритм сопряженного градиента имеет наилучшую производительность по этой проблеме, хотя все алгоритмы сопряженного градиента работают хорошо. Алгоритм LM не так хорошо выполняет эту задачу аппроксимации функции, как это было с двумя другими. Это происходит потому, что количество весов и отклонений в сети снова увеличилось (378 против 152 против 16). По мере увеличения числа параметров геометрически увеличивается требуемое в алгоритме LM вычисление.

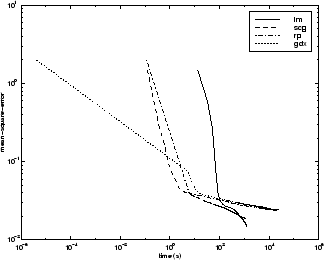
На следующем рисунке показана среднеквадратическая ошибка в зависимости от времени выполнения для некоторых типичных алгоритмов. Для этой проблемы можно увидеть, что алгоритм LM способен довести среднеквадратическую ошибку до более низкого уровня, чем другие алгоритмы. Алгоритмы SCG и RP обеспечивают самую быструю начальную сходимость.

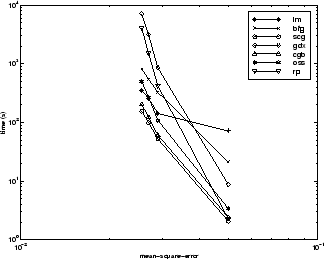
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. Можно видеть, что алгоритмы LM и BFG улучшаются относительно других алгоритмов по мере уменьшения цели ошибки.

Набор данных DIABETES

Шестой проблемой эталонного теста является проблема распознавания образов. Цель сети - решить, есть ли у человека диабет, на основе личных данных (возраст, количество беременностей) и результатов медицинских осмотров (например, артериальное давление, индекс массы тела, результат теста на толерантность к глюкозе и т.д.). Данные были получены из базы данных машинного обучения Калифорнийского университета в Ирвайне. Сеть, используемая для этой проблемы, представляет собой сеть 8-15-15-2 с нейронами тансиг во всех слоях. В следующей таблице приведены результаты обучения этой сети с использованием девяти различных алгоритмов. Каждая запись в таблице представляет 10 различных испытаний, где в каждом испытании используются разные случайные начальные веса. В каждом случае сеть обучают до тех пор, пока квадрат ошибки не станет меньше 0,05.

Алгоритмы сопряженного градиента и упругое обратное распространение обеспечивают быструю сходимость. Результаты по этой проблеме согласуются с другими рассмотренными проблемами распознавания образов. Алгоритм RP хорошо работает над всеми проблемами распознавания образов. Это разумно, потому что этот алгоритм был разработан для преодоления трудностей, вызванных тренировками с сигмоидальными функциями, которые имеют очень небольшие уклоны при работе далеко от центральной точки. Для распознавания образов используются функции переноса сигмоидов на уровне вывода, и необходимо, чтобы сеть работала в хвостах сигмоидной функции.

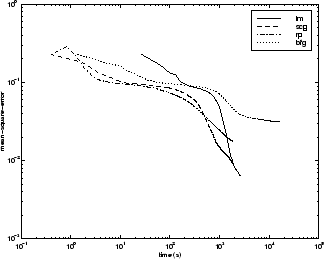
На следующем рисунке показана среднеквадратическая ошибка в зависимости от времени выполнения для некоторых типичных алгоритмов. Как и в случае с другими проблемами, вы видите, что SCG и RP имеют быструю начальную сходимость, в то время как алгоритм LM способен обеспечить меньшую конечную ошибку.

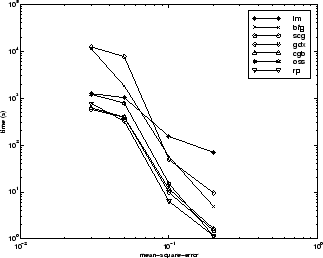
Взаимосвязь между алгоритмами дополнительно проиллюстрирована на следующем рисунке, на котором показано время, необходимое для сходимости, по сравнению со средней целью сходимости квадратной ошибки. В этом случае можно увидеть, что алгоритм BFG ухудшается по мере уменьшения цели ошибки, в то время как алгоритм LM улучшается. Алгоритм RP лучше всего, за исключением наименьшей цели ошибки, где SCG лучше.

Резюме

Существует несколько характеристик алгоритма, которые можно вывести из описанных экспериментов. В целом, на задачах аппроксимации функций, для сетей, которые содержат до нескольких сотен весов, алгоритм Левенберга-Марквардта будет иметь самую быструю сходимость. Это преимущество особенно заметно, если требуется очень точная тренировка. Во многих случаях trainlm способен получить более низкие среднеквадратические ошибки, чем любой из других протестированных алгоритмов. Однако по мере увеличения количества весов в сети преимущество trainlm уменьшается. Кроме того, trainlm производительность относительно низкая при проблемах распознавания образов. Требования к хранению trainlm больше, чем другие проверенные алгоритмы.

trainrp функция является самым быстрым алгоритмом для проблем распознавания образов. Однако он плохо выполняет задачи аппроксимации функций. Его производительность также ухудшается по мере снижения цели ошибки. Требования к памяти для этого алгоритма относительно малы по сравнению с другими рассмотренными алгоритмами.

Алгоритмы сопряженного градиента, в частности trainscg, по-видимому, выполняет более широкий спектр проблем, особенно для сетей с большим количеством весов. Алгоритм SCG почти так же быстр, как алгоритм LM по проблемам аппроксимации функций (быстрее для больших сетей) и почти так же быстр, как trainrp о проблемах распознавания образов. Его производительность снижается не так быстро, как trainrp это происходит, когда ошибка уменьшается. Алгоритмы сопряженного градиента имеют относительно скромные требования к памяти.

Производительность trainbfg аналогичен trainlm. Для этого не требуется столько ресурсов хранения, сколько trainlm, но требуемое вычисление увеличивается геометрически с размером сети, потому что эквивалент обратной матрицы должен вычисляться при каждой итерации.

Алгоритм переменной скорости обучения traingdx обычно гораздо медленнее, чем другие методы, и имеет примерно те же требования к хранению, что и trainrp, но это может быть полезно для некоторых проблем. Есть определенные ситуации, в которых лучше сходиться медленнее. Например, при использовании ранней остановки можно получить противоречивые результаты, если использовать алгоритм, который слишком быстро сходится. Возможно, будет превышена точка минимизации ошибки в наборе проверки.