Вероятностные нейронные сети

Вероятностные нейронные сети могут использоваться для задач классификации. Когда вход представлен, первый уровень вычисляет расстояния от входного вектора до обучающих входных векторов и формирует вектор, элементы которого указывают, насколько близок вход к обучающему входу. Второй уровень суммирует эти вклады для каждого класса входов, чтобы получить в качестве чистого выхода вектор вероятностей. Наконец, конкурирующая передаточная функция на выходе второго уровня выбирает максимум этих вероятностей и выдает 1 для этого класса и 0 для других классов. Архитектура этой системы показана ниже.

Сетевая архитектура

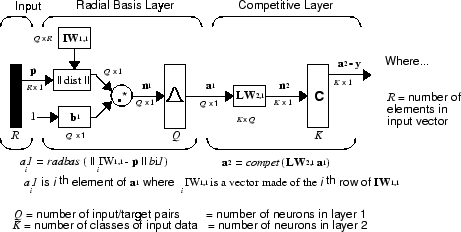
Предполагается, что существуют Q входных векторных/целевых векторных пар. Каждый целевой вектор имеет K элементы. Один из этих элементов равен 1, а остальные равны 0. Таким образом, каждый входной вектор связан с одним из K классы.

Входные веса первого уровня, ^IW1,1 (net.IW{1,1}), устанавливаются на транспонирование матрицы, сформированной из Q обучающих пар, P'. При представлении входных данных || dist || создает вектор, элементы которого указывают, насколько близки входные данные к векторам обучающего набора. Эти элементы умножаются, элемент за элементом, на смещение и посылаются в radbas передаточная функция. Входной вектор, близкий к обучающему вектору, представлен числом, близким к 1 в выходном векторе a1. Если вход близок к нескольким обучающим векторам одного класса, он представляется несколькими элементами a1, близкими к 1.

Веса второго слоя, ^LW1,2 (net.LW{2,1}), устанавливаются в матрицу Т целевых векторов. Каждый вектор имеет 1 только в строке, связанной с этим конкретным классом входных данных, и 0 в другом месте. (Использовать функцию ind2vec для создания соответствующих векторов.) Ta1 умножения суммирует элементы a1 благодаря каждому из K входные классы. Наконец, передаточная функция второго уровня, compet, создает 1, соответствующий наибольшему элементу n2 и 0 в другом месте. Таким образом, сеть классифицирует входной вектор в конкретный K класс, поскольку этот класс имеет максимальную вероятность быть правильным.

Дизайн (newpnn)

Можно использовать функцию newpnn для создания PNN. Например, предположим, что семь входных векторов и их соответствующие цели

P = [0 0;1 1;0 3;1 4;3 1;4 1;4 3]'

который дает

P =
     0     1     0     1     3     4     4
     0     1     3     4     1     1     3
Tc = [1 1 2 2 3 3 3]

который дает

Tc =
     1     1     2     2     3     3     3

Вам нужна целевая матрица с 1 в нужных местах. Вы можете получить его с помощью функции ind2vec. Это дает матрицу с 0 s, за исключением правильных точек. Так выполнять

T = ind2vec(Tc)

что дает

T =
   (1,1)        1
   (1,2)        1
   (2,3)        1
   (2,4)        1
   (3,5)        1
   (3,6)        1
   (3,7)        1

Теперь можно создать сеть и смоделировать ее с помощью входных данных. P для проверки правильности классификации. Используйте функцию vec2ind для преобразования выходных данных Y в строку Yc для уточнения классификаций.

net = newpnn(P,T);
Y = sim(net,P);
Yc = vec2ind(Y)

Это приводит к

Yc =
     1     1     2     2     3     3     3

Можно попытаться классифицировать векторы, отличные от тех, которые использовались для создания сети. Попробуйте классифицировать векторы, показанные ниже в P2.

P2 = [1 4;0 1;5 2]'
P2 =
     1     0     5
     4     1     2

Можете угадать, как эти векторы будут классифицированы? При выполнении моделирования и построении графика векторов, как и ранее, получается

Yc =
     2     1     3

Эти результаты выглядят хорошо, поскольку эти тестовые векторы были довольно близки к членам классов 2, 1 и 3 соответственно. Сети удалось обобщить свою работу для правильной классификации векторов, отличных от используемых для проектирования сети.

Возможно, потребуется попробовать классификацию PNN. В нем показано, как проектировать PNN и как сеть может успешно классифицировать вектор, не используемый в проекте.

Документация