Преобразование нижних частот с нулевым полюсным усилением в частоту M-диапазона
[Z2,P2,K2,AllpassNum,AllpassDen] = zpklp2mb(Z,P,K,Wo,Wt)
[Z2,P2,K2,AllpassNum,AllpassDen] = zpklp2mb(Z,P,K,Wo,Wt,Pass)
[Z2,P2,K2,AllpassNum,AllpassDen] = zpklp2mb(Z,P,K,Wo,Wt) возвращает нули, Z2, полюса, P2 и коэффициент усиления, K2, целевого фильтра, преобразованного из реального прототипа нижних частот путем применения Mпреобразование реальных нижних частот в реальные многополосные. По умолчанию элемент DC сохраняется в исходном местоположении.
[Z2,P2,K2,AllpassNum,AllpassDen] = zpklp2mb(Z,P,K,Wo,Wt,Pass) позволяет указать дополнительный параметр, Pass, который выбирает между использованием «DC Mobility» и «Nyquist Mobility». В первом случае элемент Nyquist остается в исходном местоположении, и элемент DC может свободно перемещаться. Во втором случае функция постоянного тока поддерживается на исходной частоте, и функция Найквиста может перемещаться.
Он также возвращает числитель, AllpassNumи знаменатель, AllpassDen, фильтра отображения allpass. Прототип фильтра нижних частот имеет нули, Z, полюса, Pи коэффициент усиления, K.
Это преобразование эффективно помещает один признак исходного фильтра, расположенного на частоте Wo, в требуемые местоположения целевой частоты, Wt1,...,WtM.
Относительные положения других элементов исходного фильтра не изменяются в целевом фильтре. Это означает, что можно выбрать два элемента исходного фильтра, F1 и F2, с F1 предшествующим F2. F1 элемента по-прежнему будет предшествовать F2 после преобразования. Однако расстояние между F1 и F2 не будет одинаковым до и после преобразования.
Выбор элемента, подлежащего этому преобразованию, не ограничивается частотой отсечения исходного фильтра нижних частот. Как правило, можно выбрать любой элемент; например, край полосы останова, DC, глубокий минимум в полосе останова или другие.
Это преобразование может также использоваться для преобразования фильтров других типов; например, режущие фильтры или резонаторы могут быть легко воспроизведены в ряде требуемых частотных местоположений. Хорошим применением является адаптивная схема подавления тональных сигналов, реагирующая на изменение количества и местоположения тональных сигналов.
Спроектируйте прототип реального полуполосного фильтра БИХ с использованием стандартного эллиптического подхода:
[b, a] = ellip(3,0.1,30,0.409); z = roots(b); p = roots(a); k = b(1); [z1,p1,k1] = zpklp2mb(z, p, k, 0.5, [2 4 6 8]/10, 'pass'); [z2,p2,k2] = zpklp2mb(z, p, k, 0.5, [2 4 6 8]/10, 'stop');
Проверьте результат, сравнив фильтр прототипа с целевым фильтром:
fvtool(b, a, k1*poly(z1), poly(p1), k2*poly(z2), poly(p2));
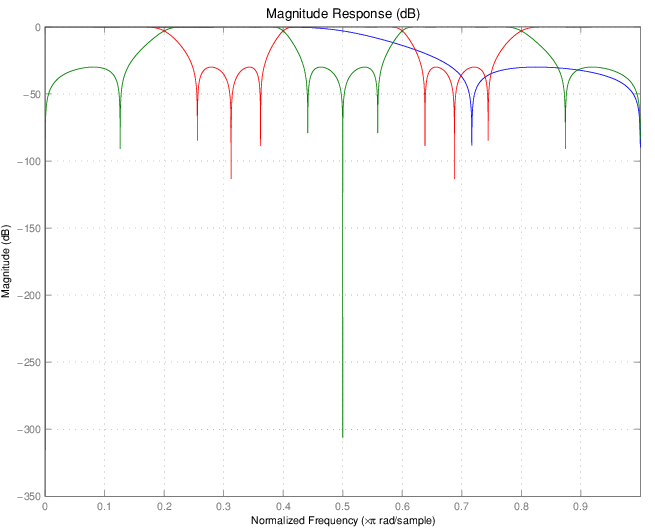
Результирующий многополосный фильтр, реплицирующий элементы прототипа, показан на рисунке. Обратите внимание на точность процесса репликации.
| Переменная | Описание |
|---|---|
Z | Нули прототипа фильтра нижних частот |
P | Полюса прототипа фильтра нижних частот |
K | Коэффициент усиления фильтра нижних частот прототипа |
Wo | Значение частоты, которое будет преобразовано из фильтра прототипа |
Wt | Требуемое местоположение частоты в преобразованном целевом фильтре |
Pass | Выбор ( |
Z2 | Нули целевого фильтра |
P2 | Полюса целевого фильтра |
K2 | Коэффициент усиления целевого фильтра |
AllpassNum | Числитель фильтра отображения |
AllpassDen | Знаменатель фильтра отображения |
Частоты должны быть нормализованы между 0 и 1, при этом 1 соответствует половине частоты дискретизации.
Franchitti, J.C., «Проблемы интерполяции и преобразования частот фильтра всех частот», MSc Thesis, департамент электротехники и вычислительной техники, Университет Колорадо, 1985.
Feyh, G., J.C. Franchitti и C.T. Mullis, «All-pass filter interpolation and frequency transformation problem», Proceedings 20th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, стр. 164-168, ноябрь 1986.
Маллис, К.Т. и Р.А. Робертс, цифровая обработка сигналов, раздел 6.7, Рединг, Массачусетс, Эддисон-Уэсли, 1987.
Feyh, G., W.B. Jones и C.T. Mullis, расширение алгоритма Шура для преобразования частот, линейных схем, систем и обработки сигналов: теория и применение, C. J. Byrnes et al Eds, Амстердам: Elsevier, 1988.