Преобразование цифровой частоты

Детали и методология

Обзор преобразований
Выбор элементов, подлежащих преобразованию
Сопоставление между фильтром прототипа и целевым фильтром
Сводка по частотным преобразованиям

Обзор преобразований

Преобразование существующих конструкций фильтров FIR или IIR в модифицированную форму IIR часто выполняется с использованием частотных преобразований allpass. Хотя полученные конструкции могут быть значительно дороже с точки зрения размерности, чем прототип (оригинальный) фильтра, их простота использования в фиксированных или переменных применениях является большим преимуществом.

Общая идея преобразования частоты состоит в том, чтобы взять существующий фильтр-прототип и создать из него другой фильтр, который сохранит некоторые характеристики прототипа, в частотной области. Функции преобразования достигают этого путем замены каждого элемента задержки фильтра прототипа фильтром allpass, тщательно разработанным таким образом, чтобы иметь заданную фазовую характеристику для достижения изменений, запрошенных проектировщиком.

Обычно используется основная форма отображения:

$_{HT} (z)_{=}_{Ho} [HA$ (z)]

_HA (z) является фильтром отображения allpass N-го порядка, задаваемым

$\begin{array}{l} _{HA} (z) \frac{_{}^{}_{}^{}}{_{}^{}_{}^{}} \frac{_{} =S∑i=0Nαiz−i∑i=0Nαiz−N+i=NA}{(_{z})} \\ {DA}_{} (z \end{array}$ ) α0 = 1

где

_Ho (z) - Передаточная функция фильтра прототипа

_HA (z) - функция передачи фильтра отображения allpass

_HT (z) - Передаточная функция целевого фильтра

Рассмотрим простой пример преобразования,

$_{HT} (z)_{=} Ho$ (− z)

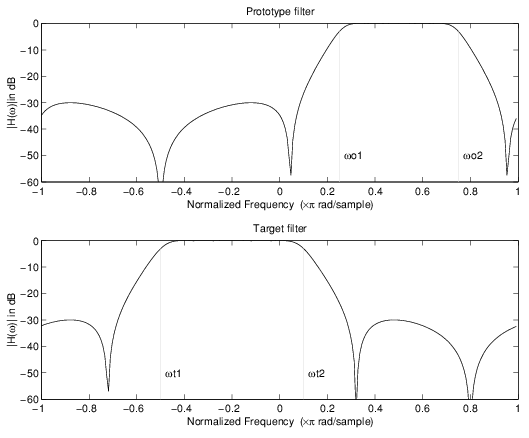
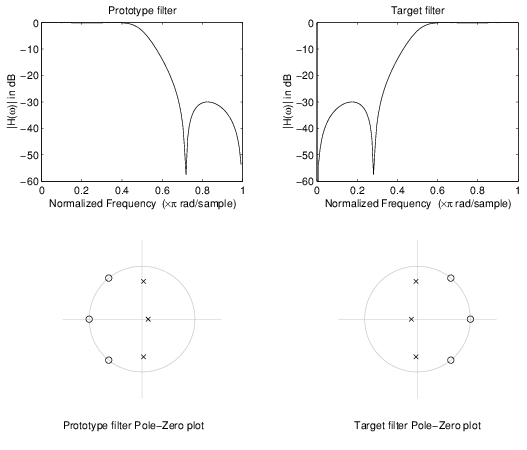
Целевой фильтр имеет свои полюса и нули, перевернутые через начало координат вещественной и мнимой осей. Для реального прототипа фильтра он даёт зеркальный эффект против 0.5, что означает, что низкочастотный _Ho (z) даёт начало действительному высокопроходному _HT (z). Это показано на следующем рисунке для прототипа фильтра, разработанного как полуполосный эллиптический фильтр третьего порядка.

Пример простого зеркального преобразования

Выбор фильтра allpass для обеспечения частотного отображения необходим для обеспечения частотного преобразования частотного отклика фильтра-прототипа на целевой фильтр путем изменения частотного положения признаков из фильтра-прототипа без влияния на общую форму отклика фильтра.

Фазовый отклик фильтра отображения, нормализованного до δ, может быть интерпретирован как функция трансляции:

$H (_{} wnew)_{=}$

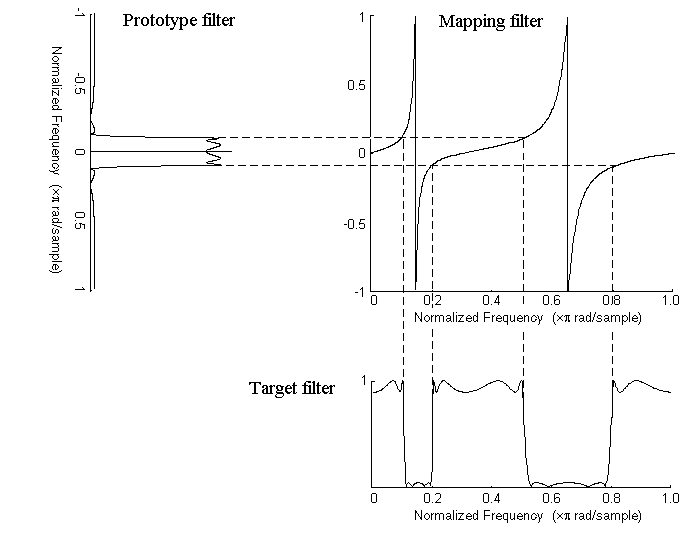
Графическая интерпретация преобразования частоты показана на рисунке ниже. Комплексное многополосное преобразование принимает действительный фильтр нижних частот и преобразует его в ряд полос пропускания вокруг единичной окружности.

Графическая интерпретация процесса отображения

Большая часть частотных преобразований основана на фильтре отображения allpass второго порядка:

$_{HA} (z) \frac{= \pm_{} 1^{+}_{} {α1z}^{−}}{_{1} +_{}^{α2z} -^{}}$ 2α2 + α1z − 1 + z − 2

Две степени свободы, обеспечиваемые выбором _α1 и _α2, не полностью используются обычным ограничительным набором классических отображений «плоского верха», таких как низкочастотное преобразование в полосовое. Вместо этого любые два признака передаточной функции могут быть перенесены в (почти) любые два других частотных местоположения, если _α1 и _α2 выбраны так, чтобы поддерживать полюса _HA (z) строго вне единичной окружности (так как _HA (z) заменяется на z в прототипе передаточной функции). Более того, как впервые указал Константинид, выбор внешнего знака влияет на то, можно ли переместить исходный признак в ноль (знак минус, условие, известное как «подвижность постоянного тока») или можно перенести частоту Найквиста (случай «подвижности Найквиста», возникающий, когда ведущий знак является положительным).

Выбор элементов, подлежащих преобразованию

Выбор соответствующего преобразования частоты для достижения требуемого эффекта и правильных характеристик прототипа фильтра очень важен и требует тщательного рассмотрения. Не рекомендуется использовать преобразование первого порядка для управления несколькими функциями. Фильтр сопоставления не обеспечит достаточной гибкости. Также нехорошо использовать преобразование более высокого порядка только для изменения частоты отсечки фильтра нижних частот. Увеличение порядка фильтров будет слишком большим, без учета дополнительной реплики прототипа фильтра, которая может быть создана в нежелательных местах.

Выбор функций для преобразования реальных нижних частот в полосу пропускания

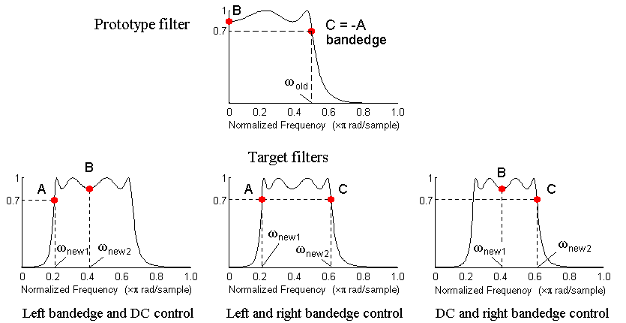
Для иллюстрации идеи действительное многоточечное преобразование второго порядка было применено три раза к одному и тому же эллиптическому полуполосному фильтру, чтобы превратить его в полосовой фильтр. В каждом из трех случаев были выбраны два различных признака прототипа фильтра для получения полосового фильтра с полосой пропускания от 0,25 до 0,75. Положение элемента постоянного тока не было важным, но было бы выгодно, если бы он находился посередине между краями полосы пропускания в целевом фильтре. В первом случае выбранными признаками были левый и правый края полосы пропускания фильтра нижних частот, во втором случае - левый край полосы пропускания и постоянный ток, в третьем случае - постоянный ток и правый край полосы пропускания.

Результат выбора различных функций

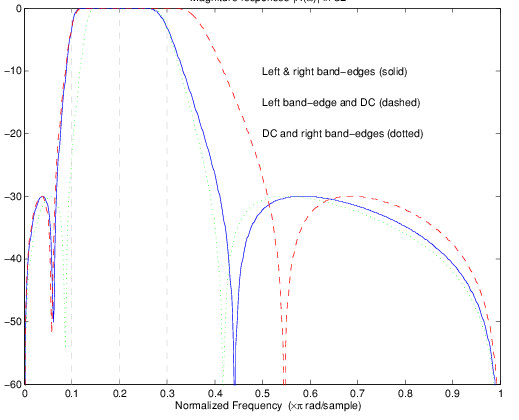
Результаты всех трех подходов совершенно разные. Для каждого из них только выбранные элементы позиционировались точно там, где они требовались. В первом случае DC перемещается к левому краю полосы пропускания так же, как и все другие элементы, близкие к левому краю, зажатому там. Во втором случае правый край полосы пропускания был вытолкнут из ожидаемой цели, поскольку требовалось точное положение постоянного тока. В третьем случае левый край полосы пропускания тянут к постоянному току, чтобы расположить его на правильной частоте. Вывод состоит в том, что если в полосе пропускания может находиться только DC, то для преобразования должны быть выбраны края полосы пропускания. Для большинства случаев, требующих позиционирования проходов и стоп-полос, конструкторы всегда должны выбирать положение кромок фильтра-прототипа, чтобы убедиться, что они получают края целевого фильтра в правильных местах. Частотные ответы для трех рассмотренных случаев показаны на рисунке. Прототип фильтра представлял собой эллиптический фильтр нижних частот третьего порядка с частотой отсечки 0,5.

Здесь приведен код MATLAB ®, используемый для создания рисунка.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В данном примере требования установлены для создания реального полосового фильтра с краями полосы пропускания 0,1 и 0,3 из реального полосового фильтра, имеющего частоту отсечки 0,5. Это делается тремя различными способами. В первом приближении выбирают оба края полосы пропускания, во втором приближении выбирают левый край полосы пропускания и постоянный ток, в то время как в третьем приближении принимают постоянный ток и правый край полосы пропускания:

[num1,den1] = iirlp2xn(b, a, [-0.5, 0.5], [0.1, 0.3]);
[num2,den2] = iirlp2xn(b, a, [-0.5, 0.0], [0.1, 0.2]);
[num3,den3] = iirlp2xn(b, a, [ 0.0, 0.5], [0.2, 0.3]);

Сопоставление между фильтром прототипа и целевым фильтром

В общем, частотное отображение преобразует фильтр-прототип _Ho (z) в целевой фильтр, _HT (z), используя фильтр allpass NA-го порядка, HA (z). Общая форма фильтра отображения allpass приведена в разделе Обзор преобразований. Частотное отображение является математической операцией, которая заменяет каждый слой фильтра прототипа фильтром allpass. Существует два способа выполнения такого отображения. Выбор подхода зависит от того, как представлены прототипы и целевые фильтры.

При задании фильтра-прототипа N-го порядка с полюсно-нулевой формой

$_{Ho} (z) \frac{_{}^{} =∑i=1N (_{z}}{-_{zi}^{)}_{} \sumi=1N}$ (z − pi)

отображение заменяет каждый полюс, _pi, и каждый ноль, _zi, на число полюсов и нулей, равное порядку фильтра отображения allpass:

$_{Хо} (z) \frac{_{}^{} =∑i=1N_{(}^{}_{}^{}_{}_{}^{}_{}^{}^{}}{_{S∑k=0N−1αkzk−zi⋅∑k=0N−1αkzN−k)}^{}_{∑i=1N (}^{}_{}^{}_{}_{}^{}_{}^{}^{}}$ S∑k=0N−1αkzk−pi⋅∑k=0N−1αkzN−k)

Для поиска полюсов и нулей целевого фильтра необходимо использовать корневой поиск в выражениях в скобках.

При описании фильтра прототипа в форме числитель-знаменатель:

$_{HT} (z) {\frac{_{=}^{}_{β0zN}^{+} β1zN_{-}}{_{1}^{+} . ._{.}^{+}_{βNα0zN}}}_{+_{} α1zN}$ − 1 +... + αN 'z = HA (z)

Тогда процесс отображения потребует ряд сверток, чтобы вычислить числитель и знаменатель целевого фильтра:

$_{HT} (z) \frac{_{=}_{} {β1NA}^{} (z_{)}_{N} +^{} {β2NA}_{} (z) N -_{}_{} {1DA (}^{z}}{)_{} +_{.} {. .}^{+}_{}_{βNDA} {(z}^{)}_{} Nβ1NA (z)_{N}_{+}^{}}$ β2NA (z) N − 1DA (z) +... + βNDA (z) N

Для каждого коэффициента _αi и _βi фильтра-прототипа многочлены _{NAth-порядка} должны быть свернуты N времена. Такой подход может вызвать ошибки округления для больших фильтров прототипа и/или фильтров отображения высокого порядка. В этом случае пользователь должен рассмотреть альтернативу выполнения отображения с использованием полюсов и нулей.

Сводка по частотным преобразованиям

Преимущества

Большинство частотных преобразований описываются решениями замкнутой формы или могут быть вычислены из набора линейных уравнений.
Они дают предсказуемые и знакомые результаты.
Высоты пульсаций из фильтра прототипа сохраняются в целевом фильтре.
Они архитектурно привлекательны для переменных и адаптивных фильтров.

Недостатки

Бывают случаи, когда использование методов оптимизации для проектирования требуемого фильтра дает лучшие результаты.
Преобразования высокого порядка увеличивают размерность целевого фильтра, что может дать дорогостоящие конечные результаты.
Начиная со свежих конструкций, можно избежать взаимных компромиссов.

Частотные преобразования для реальных фильтров

Обзор
Сдвиг реальной частоты
От реальных нижних частот до реальных нижних частот
От реального нижнего к реальному верхнему
Реальный нижний проход к реальному бандпасу
Реальный нижний проход к реальному бандстопу
Реал Lowpass в Real Multiband
От реальных нижних частот до реальных многоточечных

Обзор

В этом разделе рассматриваются преобразования реальных частот, которые принимают фильтр прототипа реальных нижних частот и преобразуют его в другой фильтр реальных целей. Целевой фильтр имеет свою частотную характеристику, модифицированную по отношению к частотной характеристике фильтра-прототипа в соответствии с характеристикой применяемого преобразования частоты.

Сдвиг реальной частоты

Преобразование с действительным сдвигом частоты использует фильтр отображения allpass второго порядка. Он выполняет точное отображение одного выбранного признака частотной характеристики в его новое местоположение, дополнительно перемещая как признаки Найквиста, так и признаки постоянного тока. Это эффективно перемещает весь отклик фильтра нижних частот на расстояние, заданное выбором элемента из фильтра прототипа и целевого фильтра. Как реальная трансформация, она работает аналогичным образом для положительных и отрицательных частот.

$_{HA} (z)^{} \frac{^{}}{^{}}$ =z−1⋅1−αz−1α−z−1

с α, заданным

$α = \begin{array}{l} \frac{{\frac{}{} {cosíd2}_{(} {startold}_{-}}{\frac{2startnew}{)}_{}} & \frac{}{}_{} cosā2objectoldfor 'cosā2 (_{} startold - \\ \frac{\frac{}{2startnew})_{| <}_{} 1sinè2}{(\frac{}{} {startold}_{-}} & 2startnew) \end{array}$ sinā2ü oldotherwise

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew - Положение элемента первоначально в _{λ old} в целевом фильтре

В следующем примере показано, как это преобразование можно использовать для перемещения отклика фильтра нижних частот прототипа в любом направлении. Обратите внимание, что, поскольку целевой фильтр также должен быть реальным, реакция целевого фильтра будет по своей природе нарушаться на частотах, близких к Nyquist и близких к DC. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования элемент перемещается от 0,5 до 0,9:

[num,den] = iirshift(b, a, 0.5, 0.9);

Пример отображения реального сдвига частоты

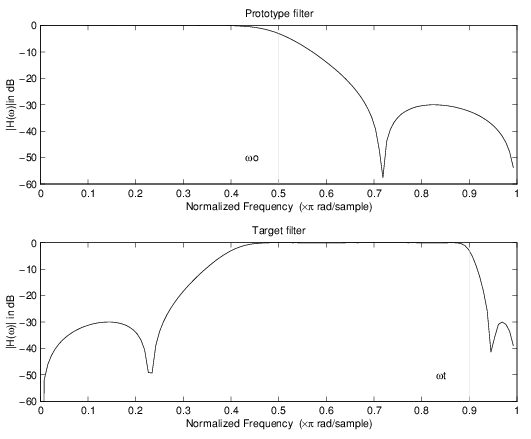
От реальных нижних частот до реальных нижних частот

В преобразовании фильтра реальных нижних частот в фильтр реальных нижних частот используется фильтр отображения allpass первого порядка. Он выполняет точное отображение одного признака частотной характеристики в новое местоположение, сохраняя фиксированные признаки DC и Nyquist. Как реальная трансформация, она работает аналогичным образом для положительных и отрицательных частот. Важно отметить, что использование отображения первого порядка гарантирует, что порядок фильтра после преобразования будет таким же, как и первоначально.

$_{HA} (z) = \frac{- (^{1}}{-^{αz}} -$ 1α − z − 1)

с α, заданным

$α \frac{= \frac{}{} {siníd2}_{(}_{ü old -}}{\frac{startnew}{)}_{} sinā2_{(}}$ startold − startnew)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew - Частотное расположение одного и того же элемента в целевом фильтре

В приведенном ниже примере показано, как изменить частоту отсечения фильтра прототипа. Код MATLAB для этого примера показан на следующем рисунке.

Фильтр-прототип представляет собой полуполосный эллиптический, вещественный фильтр третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Частота отсечки изменяется от 0,5 до 0,75:

[num,den] = iirlp2lp(b, a, 0.5, 0.75);

Пример отображения реальных нижних частот в реальные нижние частоты

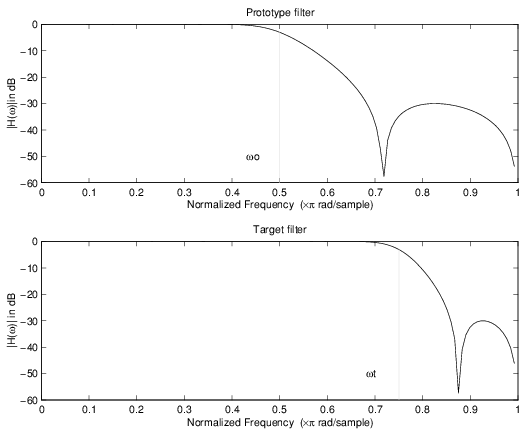
От реального нижнего к реальному верхнему

В преобразовании реального фильтра нижних частот в реальный фильтр верхних частот используется фильтр отображения allpass первого порядка. Он выполняет точное отображение одного признака частотной характеристики в новое местоположение, дополнительно заменяя элементы DC и Nyquist. Как реальная трансформация, она работает аналогичным образом для положительных и отрицательных частот. Так же, как и в предыдущем преобразовании из-за использования отображения первого порядка, порядок фильтра до и после преобразования тот же.

$_{HA} (z) = \frac{- (^{1}}{+^{αz}} -$ 1α + z − 1)

с α, заданным

$α = \frac{− (\frac{}{}_{cosíd2 (}_{startold} +}{\frac{}{startnew})_{} {cos.d2}_{(}}$ startold − startnew))

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew - Частотное расположение одного и того же элемента в целевом фильтре

В приведенном ниже примере показано, как преобразовать фильтр нижних частот в фильтр верхних частот с произвольно выбранной частотой отсечения. В приведенном ниже коде MATLAB фильтр нижних частот преобразуется в верхний канал с частотой отсечки, смещенной от 0,5 до 0,75. Результаты показаны на рисунке.

Фильтр-прототип представляет собой полуполосный эллиптический, вещественный фильтр третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Пример перемещает частоту отсечки от 0,5 до 0,75:

[num,den] = iirlp2hp(b, a, 0.5, 0.75);

Пример сопоставления реального нижнего и реального верхних частот

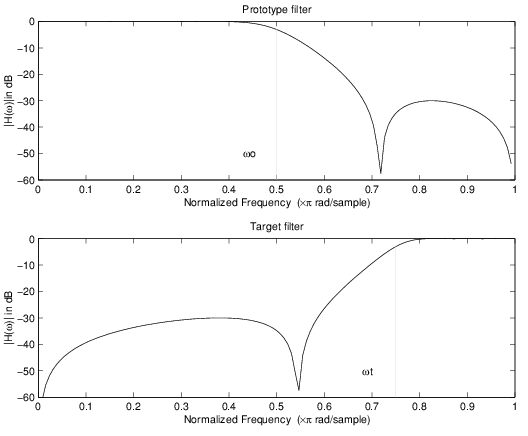
Реальный нижний проход к реальному бандпасу

В преобразовании реального фильтра нижних частот в реальный полосовой фильтр используется фильтр отображения allpass второго порядка. Он выполняет точное отображение двух признаков частотной характеристики в их новое местоположение, дополнительно перемещая элемент постоянного тока и сохраняя элемент Найквиста фиксированным. Как реальная трансформация, она работает аналогичным образом для положительных и отрицательных частот.

$_{HA} (z) = \frac{- (1 - β^{(} 1 +^{α}}{) z − 1 -^{} αz^{-}}$ 2α − β (1 + α) z − 1 + z − 2)

с α и β, заданными

$α \frac{= \frac{}{} siníd4_{(}_{2ü old -}_{startnew, 2} +}{\frac{}{startnew}, 1_{)}_{sinā4 (}_{2startold +}}$ startnew, 2 − startnew, 1)

$β = \frac{}{} {cosā2}_{(«} новый»,_{1 + «}$ новый», 2)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew, 1 - Исходное положение элемента в целевом фильтре (-_{ü old)}

_startnew, 2 - Исходное положение элемента в целевом фильтре (+ _startold)

В приведенном ниже примере показано, как переместить отклик фильтра нижних частот прототипа в любом направлении. Обратите внимание, что, поскольку целевой фильтр также должен быть реальным, реакция целевого фильтра будет по своей природе нарушаться на частотах, близких к Nyquist и близких к DC. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создается полоса пропускания от 0,5 до 0,75:

[num,den] = iirlp2bp(b, a, 0.5, [0.5, 0.75]);

Пример преобразования реальных нижних частот в реальные полосы пропускания

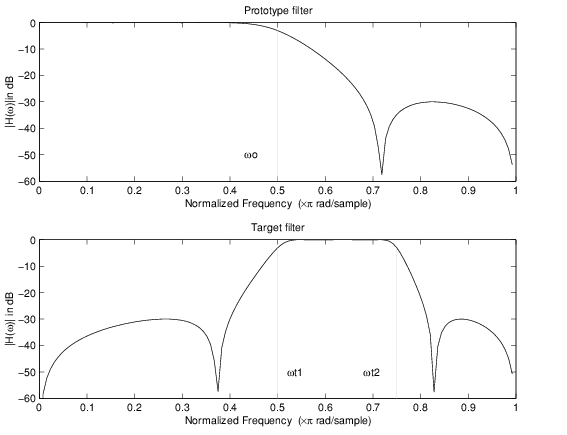
Реальный нижний проход к реальному бандстопу

В преобразовании реального фильтра нижних частот в реальный полосовой фильтр используется фильтр отображения allpass второго порядка. Он выполняет точное отображение двух признаков частотной характеристики в их новое местоположение, дополнительно перемещая элемент Найквиста и сохраняя неизменным элемент постоянного тока. Это эффективно создает полосу останова между выбранными частотными местоположениями в целевом фильтре. Как реальная трансформация, она работает аналогичным образом для положительных и отрицательных частот.

$_{HA} (z) \frac{= 1 - β^{(1} +^{α)}}{z - 1 +^{αz} -^{}}$ 2α − β (1 + α) z − 1 + z − 2

с α и β, заданными

$\begin{array}{l} α \frac{= \frac{}{} cosíd4_{(}_{2startold +}_{startnew, 2} -}{\frac{}{startnew}, 1_{)}_{cosā4 (}_{2startold -}} \\ startnew, \frac{2}{} +_{startnew,} 1_{) β =} \end{array}$ cos.d2 (startnew, 1 + startnew, 2)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew, 1 - Исходное положение элемента в целевом фильтре (-_{ü old)}

_startnew, 2 - Исходное положение элемента в целевом фильтре (+ _startold)

В следующем примере показано, как это преобразование может быть использовано для преобразования прототипа фильтра нижних частот с частотой отсечки 0,5 в реальный полосовой фильтр с той же самой структурой пульсации полосы пропускания и полосы останова, и полоса останова расположена между 0,5 и 0,75. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создается полоса останова от 0,5 до 0,75:

[num,den] = iirlp2bs(b, a, 0.5, [0.5, 0.75]);

Пример отображения реальных нижних частот в реальные полосы пропускания

Реал Lowpass в Real Multiband

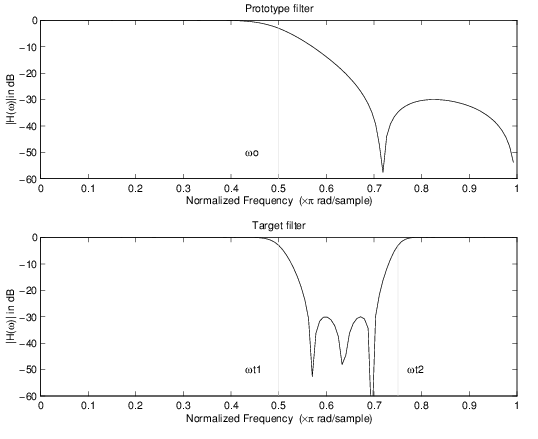
Это преобразование высокого порядка выполняет точное отображение одного выбранного признака частотной характеристики фильтра прототипа в ряд новых местоположений в целевом фильтре. Его наиболее распространенное использование состоит в преобразовании реальных нижних частот с предопределенными полосой пропускания и пульсациями стоп-полосы в реальный многополосный фильтр с N произвольными краями полосы, где N - порядок фильтра отображения allpass.

$\begin{array}{l} _{HA} (z) \frac{_{}^{}_{}^{}^{}}{_{}^{}_{}^{}^{}} \\ _{} \end{array}$ =S∑i=0Nαiz−i∑i=0Nαiz−N+iα0=1

Коэффициенты α задаются

${\begin{cases} \begin{matrix} _{} & α0=1k=1 ... \end{matrix} \\ ,_{} \frac{\frac{}{} Nαk =−Ssinπ2_{(} {Nωnew +}^{}_{(−1)}}{\frac{kωold}{)} sinπ2 (_{}^{}_{(N−2k) ωnew +}} \end{cases}$ (−1) kωold)

где

_{λ old,} k - Частотное расположение первой функции в фильтре прототипа

_startnew, k - Положение признака первоначально в _{λ old,} k в целевом фильтре

Коэффициент мобильности S определяет мобильность или функцию DC или Nyquist:

$S = \begin{matrix} { \\ 1Nyquist & - \end{matrix}$ 1DC

Пример ниже показывает, как это преобразование может быть использовано для преобразования прототипа фильтра нижних частот с частотой отсечки 0,5 в фильтр, имеющий ряд полос, расположенных на произвольных граничных частотах 1/5, 2/5, 3/5 и 4/5. Параметр S был таков, что при DC существует полоса пропускания. Вот код MATLAB для создания рисунка.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Пример преобразования создает три стопбенда, от DC до 0,2, от 0,4 до 0,6 и от 0,8 до Nyquist:

[num,den] = iirlp2mb(b, a, 0.5, [0.2, 0.4, 0.6, 0.8], `pass');

Пример преобразования реальных нижних частот в реальные многополосные

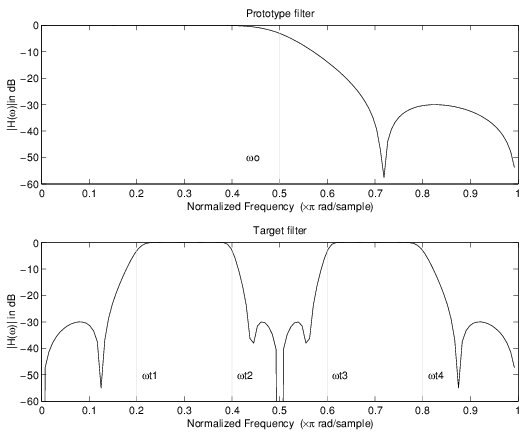
От реальных нижних частот до реальных многоточечных

Это частотное преобразование высокого порядка выполняет точное отображение ряда выбранных признаков частотной характеристики фильтра-прототипа на их новые местоположения в целевом фильтре. Фильтр отображения задается общей полиномиальной формой БИХ передаточной функции, как указано ниже.

$\begin{array}{l} _{HA} (z) \frac{_{}^{}_{}^{}}{_{}^{}_{}^{}} \\ _{} \end{array}$ =S∑i=0Nαiz−i∑i=0Nαiz−N+iα0=1

Для многоточечного частотного преобразования N-го порядка коэффициенты α равны

${\begin{array}{l} _{}^{}_{}_{}_{}^{}_{}^{}_{}_{} \\ _{}^{_{}} \\ _{}^{_{}} \\ ∑i=1NαN−izold,k⋅znew,ki−S⋅znew,kN−i=−zold,k−S⋅znew,kzold,k=ejπωold,kznew,k=ejπωnew,kk=1, . . . \end{array}$ , N

где

_{λ old,} k - Частотное расположение первой функции в фильтре прототипа

_startnew, k - Положение признака первоначально в _{λ old,} k в целевом фильтре

Коэффициент мобильности S определяет мобильность функции DC или Nyquist:

$S = \begin{matrix} { \\ 1Nyquist & - \end{matrix}$ 1DC

В приведенном ниже примере показано, как это преобразование может быть использовано для перемещения элементов прототипа фильтра нижних частот первоначально при -0.5 и 0.5 в их новые местоположения при 0.5 и 0.75, эффективно изменяя положение полосы пропускания фильтра. Вот код MATLAB для создания рисунка.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создается полоса пропускания от 0,5 до 0,75:

[num,den] = iirlp2xn(b, a, [-0.5, 0.5], [0.5, 0.75], `pass');

Пример преобразования реальных нижних частот в реальные многоточечные

Частотные преобразования для сложных фильтров

Обзор
Комплексный сдвиг частоты
От реального нижнего до сложного полосы пропускания
От реальных нижних частот до сложных полос пропускания
От реальных нижних частот до сложных многополосных
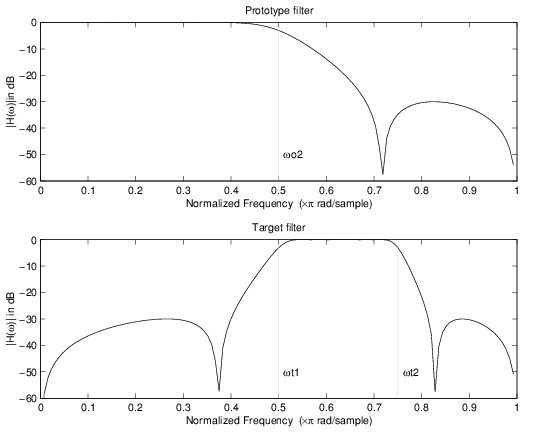
От реальных нижних частот до сложных многоточечных соединений
Комплексный полосовой переход в комплексный полосовой переход

Обзор

В этом разделе рассматривается комплексное преобразование частоты, которое принимает комплексный фильтр прототипа и преобразует его в другой комплексный целевой фильтр. Целевой фильтр имеет свою частотную характеристику, модифицированную по отношению к частотной характеристике фильтра-прототипа согласно характеристике применяемого преобразования частоты из:

Комплексный сдвиг частоты

Комплексное частотное преобразование является простейшим преобразованием первого порядка, которое выполняет точное отображение одного выбранного признака частотной характеристики в его новое местоположение. При этом он поворачивает весь отклик фильтра нижних частот прототипа на расстояние, заданное выбором признака из фильтра прототипа и целевого фильтра.

$_{HA} (z) =^{}$ αz − 1

с α, заданным

$α =^{{ej2δ}_{(«}_{новый» − «}}$ старый»)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew - Положение элемента первоначально в _{λ old} в целевом фильтре

Частным случаем комплексного сдвига частоты является, так называемый, трансформатор Гильберта. Его можно сконструировать, установив для параметра значение | α | = 1, то есть

$α = \begin{matrix} { \\ 1 вперед & - \end{matrix}$ 1 внутрь

В приведенном ниже примере показано, как применить это преобразование для поворота отклика фильтра нижних частот прототипа в любом направлении. Обратите внимание, что поскольку преобразование может быть достигнуто простым оператором фазового сдвига, все функции фильтра прототипа будут перемещены на одну и ту же величину. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования элемент перемещается от 0,5 до 0,3:

[num,den] = iirshiftc(b, a, 0.5, 0.3);

Пример отображения сложного сдвига частоты

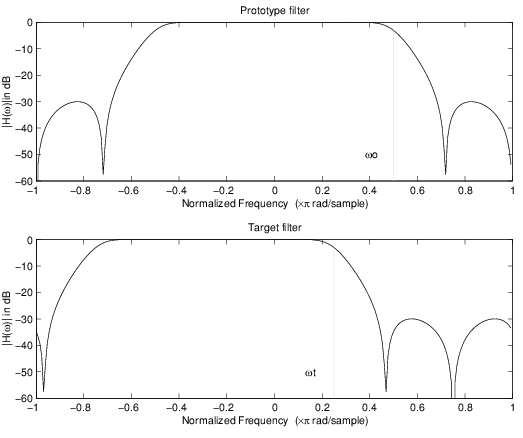
От реального нижнего до сложного полосы пропускания

Это преобразование первого порядка выполняет точное отображение одного выбранного признака частотной характеристики фильтра прототипа в два новых местоположения в целевом фильтре, создавая полосу пропускания между ними. Функции Nyquist и DC могут быть перемещены вместе с остальной частотной характеристикой.

$_{HA} (z) \frac{= β^{−}}{^{αz} -}$ 1z − 1 − αβ

с α и β даны

$\begin{array}{l} α \frac{= \frac{}{} siníd4_{(}_{2ü old -}_{startnew, 2} +}{startnew,_{1)}_{sinλ (}_{2ü old +}} \\ {startnew}^{, 2 -_{} {startnew}_{, 1})} \end{array}$ β = e − jλ (startnew − startold)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew, 1 - Исходное положение элемента в целевом фильтре (-_{ü old)}

_startnew, 2 - Исходное положение элемента в целевом фильтре (+ _startold)

Следующий пример показывает использование такого преобразования для преобразования вещественного полуполосного фильтра нижних частот в комплексный полосовой фильтр с краями полос 0,5 и 0,75. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа представляет собой полуполосный эллиптический, реальный фильтр нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование создает полосу пропускания от 0,5 до 0,75:

[num,den] = iirlp2bpc(b, a, 0.5, [0.5 0.75]);

Пример преобразования реальных нижних частот в сложные полосы пропускания

От реальных нижних частот до сложных полос пропускания

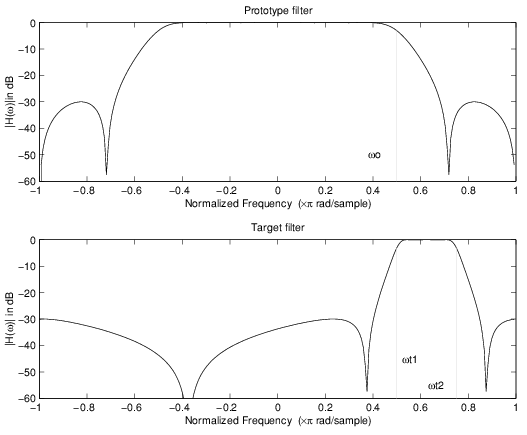
Это преобразование первого порядка выполняет точное отображение одного выбранного признака частотной характеристики фильтра прототипа в два новых местоположения в целевом фильтре, создавая между ними полосу останова. Функции Nyquist и DC могут быть перемещены вместе с остальной частотной характеристикой.

$_{HA} (z) \frac{= β^{−}}{αz^{-}}$ 1αβ − z − 1

с α и β даны

$\begin{array}{l} α \frac{= cospi_{(}_{2startold +}_{startnew, 2} -}{startnew,_{1)}_{cosλ (}_{2ü old -}} \\ {startnew}^{, 2 +_{} {startnew}_{, 1})} \end{array}$ β = e − jλ (startnew − startold)

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew, 1 - Исходное положение элемента в целевом фильтре (-_{ü old)}

_startnew, 2 - Исходное положение элемента в целевом фильтре (+ _startold)

В приведенном ниже примере показано использование такого преобразования для преобразования вещественного полуполосного фильтра нижних частот в комплексный полосовой фильтр с краями полос 0,5 и 0,75. Вот код MATLAB для генерации примера на рисунке.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование создает полосу останова от 0,5 до 0,75:

[num,den] = iirlp2bsc(b, a, 0.5, [0.5 0.75]);

Пример преобразования реальных нижних частот в сложные полосы пропускания

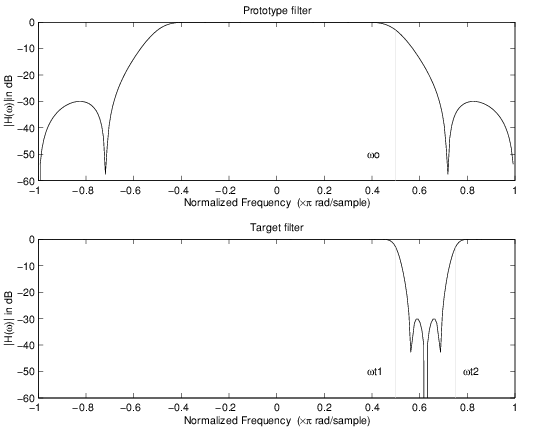
От реальных нижних частот до сложных многополосных

Это преобразование высокого порядка выполняет точное отображение одного выбранного признака частотной характеристики фильтра прототипа в ряд новых местоположений в целевом фильтре. Его наиболее распространенное использование состоит в преобразовании реальных нижних частот с предопределенными полосами пропускания и полосами останова в многополосный фильтр с произвольными границами полос. Порядок отображения фильтра должен быть четным, что соответствует четному числу ребер полосы в целевом фильтре. Фильтр отображения комплексных allpass N-го порядка задается следующей формой общей передаточной функции:

$\begin{array}{l} _{HA} (z) \frac{_{}^{}_{}^{}}{_{}^{}_{}^{}} \\ _{} \end{array}$ =S∑i=0Nαiz−i∑i=0Nαi±z−N+iα0=1

Коэффициенты α вычисляются из системы линейных уравнений:

${\begin{cases} _{}^{} ∑i=1Nℜ (_{} αi)_{}_{} {⋅[cosβ1,k−cosβ2,k]+ℑ}_{} (αi)_{}_{}_{} \\ _{}^{}_{} \cdot[sinβ1,k+sinβ2,k]=cosβ3,k\sumi=1Nℜ (αi)_{}_{}_{} \cdot[sinβ1,k-sinβ2,k]-ℑ ({αi}_{)}_{}_{} \\ _{}_{}^{}_{⋅[cosβ1,k+cosβ2,k]=sinβ3,kβ1,k=−π[νold⋅ (-} 1) к + \\ _{} к новый, к (N_{- k)]} \\ _{}_{}^{}_{} \\ β2,k=-π[ΔC+νnew,kk]β3,k=-π[νold\cdot \end{cases}$ (− 1) к + к новый, кН] к = 1... N

где

_startold - частотное расположение выбранного элемента в фильтре прототипа;

_startnew, i - Положение элементов первоначально при ± _startold в целевом фильтре

Параметр S - это дополнительный коэффициент поворота на частотное расстояние ΔC, обеспечивающий дополнительную гибкость достижения требуемого отображения:

$S =^{e -}$ jāΔC

Пример показывает использование такого преобразования для преобразования прототипа реального фильтра нижних частот с частотой отсечки 0,5 в многополосный комплексный фильтр с границами полос 0,2, 0,4, 0,6 и 0,8, создавая две полосы пропускания вокруг единичной окружности. Вот код MATLAB для создания рисунка.

Пример преобразования реальных нижних частот в сложные многополосные

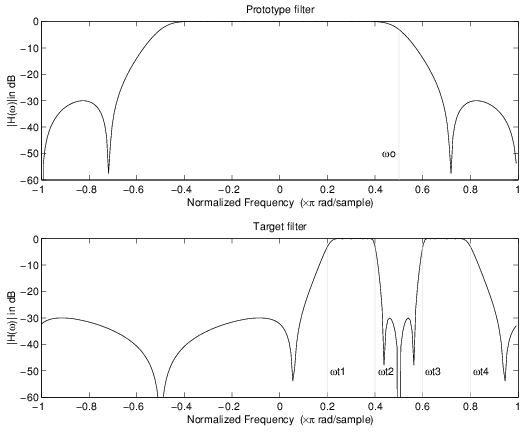
Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создаются две сложные полосы пропускания:

[num,den] = iirlp2mbc(b, a, 0.5, [0.2, 0.4, 0.6, 0.8]);

От реальных нижних частот до сложных многоточечных соединений

Это преобразование высокого порядка выполняет точное отображение ряда выбранных признаков частотной характеристики фильтра прототипа на их новые местоположения в целевом фильтре. Фильтр отображения комплексных allpass N-го порядка задается следующей формой общей передаточной функции.

$\begin{array}{l} _{HA} (z) \frac{_{}^{}_{}^{}}{_{}^{}_{}^{}} \\ _{} \end{array}$ =S∑i=0Nαiz−i∑i=0Nαi±z−N+iα0=1

Коэффициенты α могут быть вычислены из системы линейных уравнений:

${\begin{cases} _{}^{} ∑i=1Nℜ (_{} αi)_{}_{} {⋅[cosβ1,k−cosβ2,k]+ℑ}_{} (αi)_{}_{}_{} \\ _{}^{}_{} \cdot[sinβ1,k+sinβ2,k]=cosβ3,k\sumi=1Nℜ (αi)_{}_{}_{} \cdot[sinβ1,k-sinβ2,k]-ℑ ({αi}_{)}_{}_{} \\ _{} \frac{}{}_{}_{} \\ _{⋅[cosβ1,k+cosβ2,k]=sinβ3,kβ1,k=−π2[ωold,k+ωnew,k (} N \frac{-}{} k)] {β2}_{, k =} - \\ _{c.2 2} [\frac{}{2ΔC} +_{startnew},_{kk]} β3, \\ k = \end{cases}$ − c.2 2 [startold, k + startnew, kN] k = 1... N

где

_{λ old,} k - Частотное расположение первой функции в фильтре прототипа

_startnew, k - Положение признака первоначально в _{λ old,} k в целевом фильтре

$S =^{e -}$ jāΔC

В следующем примере показано, как это преобразование может быть использовано для перемещения одного выбранного признака фильтра нижних частот прототипа первоначально на -0,5 к двум новым частотам -0,5 и 0,1, а второй признак фильтра прототипа - от 0,5 к новым местоположениям на -0,25 и 0,3. Это создает две несимметричные полосы пропускания вокруг единичной окружности, создавая сложный фильтр. Вот код MATLAB для создания рисунка.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создаются две несимметричные полосы пропускания:

[num,den] = iirlp2xc(b,a,0.5*[-1,1,-1,1], [-0.5,-0.25,0.1,0.3]);

Пример преобразования реальных нижних частот в комплексное многоточечное отображение

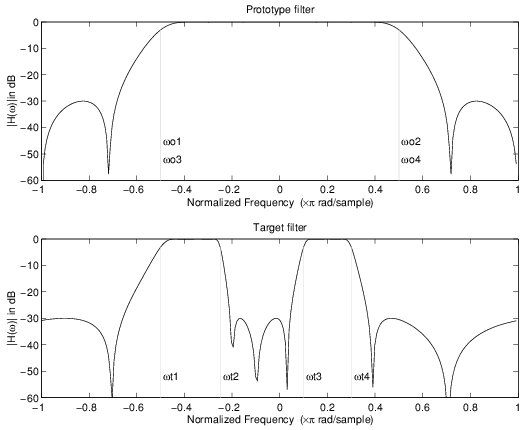
Комплексный полосовой переход в комплексный полосовой переход

Это преобразование первого порядка выполняет точное отображение двух выбранных признаков частотной характеристики фильтра прототипа в два новых местоположения в целевом фильтре. Наиболее распространенным его использованием является регулировка краев сложного полосового фильтра.

$_{HA} (z) \frac{= α (^{γ} -}{^{βz} -}$ 1) z − 1 − βγ

с α и β даны

$\begin{array}{l} α \frac{= \frac{}{} siníd4_{((} startold,_{2 -} {startold}_{, 1)} -_{(startnew},}{2 − \frac{}{} {startnew}_{, 1))}_{sinā4} ((_{startold, 2} -_{startold},} \\ 1)^{+ (_{startnew, 2} -_{startnew},} \\ 1)^{) α =_{e -} {jλ}_{(} groupold} \end{array}$ , 2 − ü old, 1) γ = e − jλ (startnew, 2 −

где

_startold, 1 - Частотное расположение первой функции в фильтре прототипа

_startold, 2 - Частотное расположение второй функции в фильтре прототипа

_startnew, 1 - Положение элемента первоначально в _{λ old,} 1 в целевом фильтре

_startnew, 2 - Положение элемента первоначально в _{λ old,} 2 в целевом фильтре

В следующем примере показано, как это преобразование можно использовать для изменения положения полосы пропускания фильтра прототипа, действительного или сложного. В приведенном ниже примере полоса пропускания фильтра прототипа охватывает от 0,5 до 0,75. Его превращали в имеющий полосу пропускания от -0,5 до 0,1. Вот код MATLAB для создания рисунка.

Фильтр прототипа является полуполосным эллиптическим, реальным фильтром нижних частот третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере преобразования создается полоса пропускания от 0,25 до 0,75:

[num,den] = iirbpc2bpc(b, a, [0.25, 0.75], [-0.5, 0.1]);

Пример комплексного преобразования полосы пропускания в комплексную полосу пропускания

Документация