Многоскоростные фильтры могут повысить эффективность конкретной реализации фильтра. В общем случае многоскоростные фильтры представляют собой фильтры, в которых различные части фильтра работают с различной скоростью. Наиболее очевидным применением такого фильтра является то, когда скорость входной выборки и скорость выходной выборки должны отличаться (прореживание или интерполяция) - однако многоскоростные фильтры также часто используются в конструкциях, где это не так. Например, вы можете иметь систему, в которой входная частота дискретизации и выходная частота дискретизации одинаковы, но внутри происходит прореживание и интерполяция в серии фильтров, так что конечный выход системы имеет ту же частоту дискретизации, что и вход. Такая конструкция может иметь более низкую стоимость, чем может быть достигнута с помощью односкоростного фильтра по различным причинам. Для получения дополнительной информации об относительных затратах на использование многоскоростных фильтров см. Harris, Fredric J., Multirate Signal Processing for Communication Systems, Prentice Hall PTR, 2004.
Фильтр, уменьшающий входную скорость, называется прореживателем. Фильтр, увеличивающий входную скорость, называется интерполятором. Чтобы визуализировать этот процесс, изучите следующий рисунок, который иллюстрирует процессы интерполяции и прореживания во временной области.
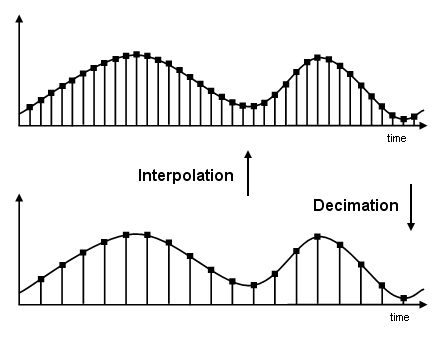
Если начать с верхнего сигнала, дискретизируется с частотой Fs, то нижний сигнал дискретизируется при Fs/2 частота. В этом случае коэффициент прореживания или Mявляется 2.
На следующем рисунке показан эффект прореживания в частотной области.
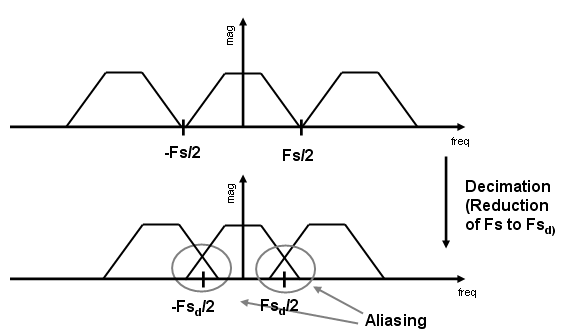
На первом рисунке на рисунке показан критически дискретизированный сигнал, т.е. частота дискретизации равна в два раза большей частотной составляющей дискретизированного сигнала. Таким образом, период сигнала в частотной области не превышает ширину полосы частот дискретизации. При уменьшении частоты дискретизации (прореживания) может происходить наложение спектров, где величины на частотах вблизи краев исходного периода становятся неразличимыми, а информация об этих значениях теряется. Чтобы обойти эту проблему, сигнал может быть отфильтрован перед процессом прореживания, избегая перекрытия спектров сигнала при Fs/2.
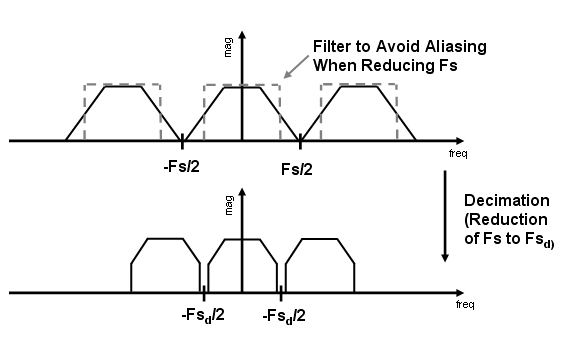
Аналогичный подход должен быть использован, чтобы избежать формирования изображения при выполнении интерполяции для дискретизированного сигнала. Дополнительные сведения о влиянии прореживания и интерполяции на дискретизированный сигнал см. в разделе Ссылки.
Ниже приводится краткое описание некоторых руководящих принципов и общих требований, касающихся прореживания и интерполяции:
Согласно теореме Найквиста, для сигналов с ограниченной полосой частот частота дискретизации должна быть по меньшей мере в два раза больше ширины полосы сигнала. Например, если имеется фильтр нижних частот с максимальной частотой 10 МГц и частотой дискретизации 60 МГц, то наибольшая частота, которая может обрабатываться системой без наложения псевдонимов, равна 60/2 = 30, что больше 10. В этом случае можно безопасно установить M = 2, так как (60/2 )/2 = 15, которое все еще больше 10.
При необходимости прореживания сигнала, не соответствующего критериям частоты, можно выполнить одно из следующих действий:
Сначала интерполировать, а затем прореживать
При прореживании сначала следует применить фильтр, а затем выполнить прореживание. При интерполяции сигнала сначала следует выполнить интерполяцию, а затем фильтрацию сигнала.
Обычно при прореживании сигнала сначала применяется фильтр, тем самым позволяя прореживать без наложения, как показано на следующем рисунке:
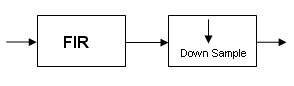
И наоборот, фильтр обычно применяется после интерполяции, чтобы избежать формирования изображения:
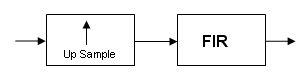
M должно быть целым числом. Хотя, если вы хотите получить M 4/5, вы можете интерполировать на 4, а затем прореживать на 5, при условии, что ограничения частоты выполнены. Этот тип многоскоростного фильтра будет называться преобразователем частоты дискретизации в следующей документации.
Многоскоростные фильтры чаще всего используются поэтапно. Этот метод представлен в следующем разделе.
[1] Fliege, N.J., Многоскоростная цифровая обработка сигналов, John Wiley and Sons, 1994.
[2] Харрис, Фредрик Джей, многоскоростная обработка сигналов для систем связи, Prentice Hall PTR, 2004.
[3] Хогенауэр, Е. Б., «Экономичный класс цифровых фильтров для децимации и интерполяции», транзакции IEEE по акустике, речи и обработке сигналов, том ASSP-29, № 2, апрель 1981, стр. 155-162.
[4] Лайонс, Ричард Г., Понимание цифровой обработки сигналов, Prentice Hall PTR, 2004
[5] Mitra, S.K., Digital Signal Processing, McGraw-Hill, 1998.
[6] Орфанидис, С.Дж., Введение в обработку сигналов, Prentice-Hall, Inc., 1996.