Субнормальные числа, ранее известные как денормальные числа в литературе с плавающей запятой, заполняют недопоток вокруг нуля в арифметике с плавающей запятой. Субнормальные значения - это особая категория значений с плавающей запятой, которые слишком близки к 0.0 для представления в виде нормированного значения. Ведущая значимость (мантисса) субнормального числа равна нулю. При сложении и вычитании чисел с плавающей запятой субнормальные числа предотвращают недотекание.
Использование субномеров обеспечивает точность за пределами нормального представления, используя первые нули в значениях для представления меньших значений после достижения представлением минимальной степени. По мере приближения стоимости 0.0, вы сравниваете точность с расширенным диапазоном. Субномеры полезны, если приложению требуется дополнительный диапазон.
Однако в системе реального времени использование субнормальных чисел может значительно увеличить задержку выполнения, что приводит к чрезмерным проектным запасам и перерасходам в реальном времени. Если моделирование или сгенерированный код выполняет вычисления, которые производят или потребляют субнормальные числа, выполнение этих вычислений может быть до 50 раз медленнее, чем аналогичные вычисления для обычных чисел. Фактическое время моделирования или выполнения кода для вычисления субномера зависит от операционной среды компьютера. Как правило, для процессоров для настольных ПК время выполнения вычислений субнормальных чисел в пять раз медленнее, чем для аналогичных вычислений обычных чисел.
Чтобы минимизировать возможность замедления выполнения или переполнения из-за задержки вычисления субнормального числа, выполните одно из следующих действий:
В модели вручную сбросьте до нуля все входящие или вычисленные субнормальные значения на входах и ключевых операциях, таких как вымывание и фильтры. Пример см. в разделе Сброс субнормальных чисел до нуля.
Чтобы определить субнормальное значение для одной точности, 32-разрядное число с плавающей запятой:
Найдите наименьшее нормированное число на хосте MATLAB ®. В окне команд введите:
>> SmallestNormalSingle = realmin('single')FLT_MIN , определено в float.h, эквивалентно realmin('single').Поиск значений в диапазоне:
0 < fabsf(x) < SmallestNormalSingle
Чтобы определить субнормальное значение для двойной точности, 64-разрядное число с плавающей запятой:
Найдите наименьшее нормированное число на хосте MATLAB. В окне команд введите:
>> SmallestNormalDouble = realmin('double') DBL_MIN , определено в float.h, эквивалентно realmin('double').Чтобы обнаружить субнормальное значение, найдите значения в этом диапазоне:
0 < fabs(x) < SmallestNormalDouble
Задайте для параметра Simulation behavior for denormal numbers значение Flush to zero (FTZ) эмулировать поведение «заподлицо к нулю» для всех денормальных результатов арифметических операций. Дополнительные сведения см. в разделе Поведение моделирования для денормальных чисел.
На вашем процессоре установите режим очистки от нуля или с помощью компилятора укажите параметр отключения субномеров. Режимы «заподлицо к нулю» рассматривают субнормальное число как 0, если оно является входом в операцию с плавающей запятой. Исключения недопотока не возникают в режиме заподлицо с нулем.
Например, в процессорах Intel ® флаги flush-to-zero (FTZ) и denormals-are-zero (DAZ) в регистре MXCSR управляют вычислениями с плавающей запятой. Для компилятора gcc в Linux , -ffast-math устанавливает резко пониженный расход (FTZ), заподлицо с нулем, в то время как –O3 -ffast-math возвращается к постепенному понижению расхода, используя субнормальные числа.
Дополнительные сведения см. в разделе Стандарт IEEE ® 754, Стандарт IEEE для арифметики с плавающей запятой.
Эта модель показывает, как использование субнормальных чисел увеличивает время моделирования в ~ 5 раз.
Откройте ex_subnormal модели. Коэффициент усиления устанавливается на субнормальное значение realmin('double')/2.
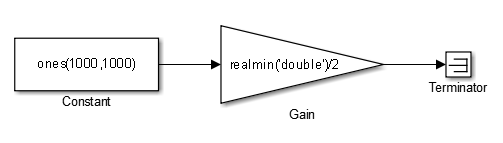
Для запуска моделирования в окне команд введите for k=1:5, tic; sim('ex_subnormal'); toc,end. Следите за временем, прошедшим при моделировании с использованием субномеров, аналогично следующему:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 9.909326 seconds. Elapsed time is 9.617966 seconds. Elapsed time is 9.797183 seconds. Elapsed time is 9.702397 seconds. Elapsed time is 9.893946 seconds.
Установите коэффициент усиления в число, 2, это не является субнормальным значением:
>> set_param('ex_subnormal/Gain', 'Gain', '2');
Для запуска моделирования в окне команд введите for k=1:5, tic; sim('ex_subnormal'); toc,end. Наблюдайте прошедшее время для моделирования, в котором не используются субнормальные значения, подобные следующим:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 2.045123 seconds. Elapsed time is 1.796598 seconds. Elapsed time is 1.758458 seconds. Elapsed time is 1.721721 seconds. Elapsed time is 1.780569 seconds.
В этом примере показано, как сбросить субнормальные числа одиночной точности до нуля.
Откройте ex_flush_to_zero модели:
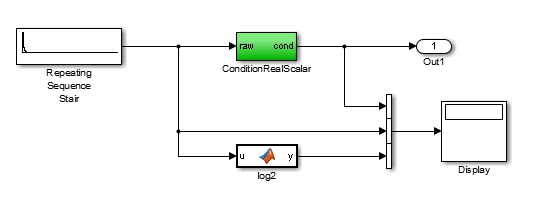
Repeating Sequence Stair генерирует последовательность чисел от двух повышенных до степени от 0 до двух повышенных до степени -165. Последовательность приближается к нулю.
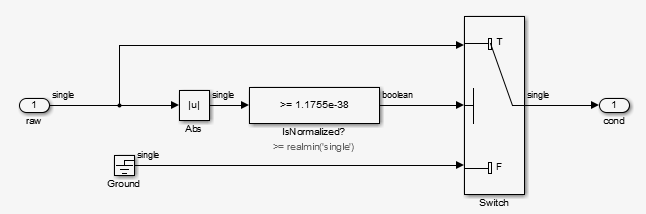
ConditionRealScalar стирает субнормальные значения одиночной точности, которые меньше realmin('single') до нуля.
Функциональный блок MATLAB log2 генерирует логарифм 2 основания Repeating Sequence Stair выход. В частности, log2 генерирует числа от 0 до -165.
На панели моделирования > Шаг назад > Настройка степпинга моделирования:
Выберите Включить возврат.
Выберите «Приостановить моделирование по достижении времени» и введите 121.
В окне модели выполните моделирование. Моделирование приостанавливается на T=121. Отображаемые значения:
ConditionRealScalar выход приближается к нулю.
Repeating Sequence Stair output приближается к нулю.
Переход к моделированию T=127. ConditionRealScalar сбрасывает субнормальное значение, выводимое из Repeating Sequence Stair до нуля.
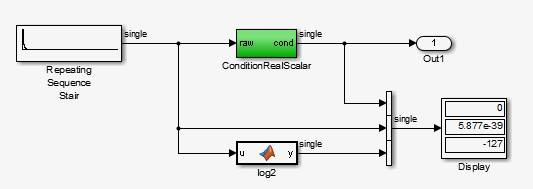
Продолжите выполнение моделирования вперед. ConditionRealScalar удаляет значения субнормальной единичной точности, выводимые из Repeating Sequence Stair до нуля. Когда T=150, выход Repeating Squence Stair сам по себе равен нулю.