Таблицы жизни используются для страхования жизни и работы с распределением вероятности человеческой смертности. Это распределение, которое зависит от возраста, имеет несколько характерных особенностей, которые являются последствиями биологических, культурных и поведенческих факторов. Обычно практики исследований жизни используют таблицы жизни, которые содержат возрастные ряды для конкретной демографии. Таблицы представлены в стандартном формате со стандартными обозначениями, характерными для области жизненных исследований. Пример таблицы жизни показан в таблице 1 из таблиц жизни CDC для Соединенных Штатов.
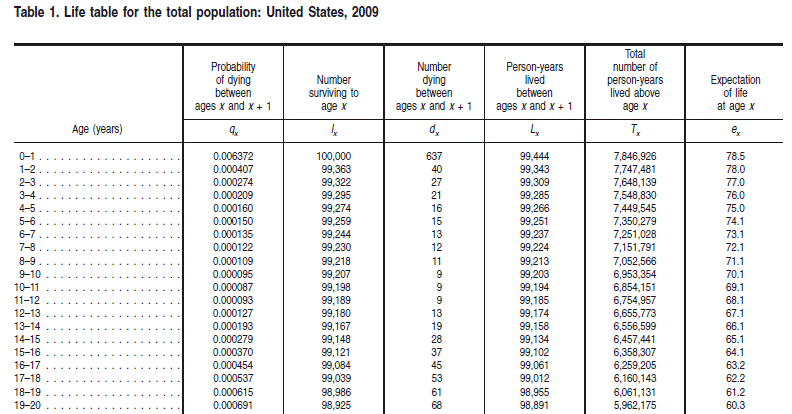
Часто эти таблицы жизненного цикла могут иметь многочисленные вариации, такие как сокращенные таблицы (которые создают проблемы из-за гранулярности данных) и различные критерии прекращения (которые могут затруднить сравнение таблиц или расчет ожидаемой продолжительности жизни).
Большинство необработанных таблиц жизненного цикла имеют одну или несколько первых трех серий в этой таблице (qx, lx и dx), и обозначение для этих трех серий является стандартным в поле.
Серия qx в основном является дискретной функцией опасности для смертности человека.
Ряд lx - это функция выживания, умноженная на радиус 100 000.
Ряд dx - это дискретная плотность вероятности для распределения как функция возраста.
Финансовые Toolbox™ могут обрабатывать произвольные данные таблицы жизни, поддерживающие несколько стандартных моделей смертности, и предоставляют различные методы интерполяции для калибровки и анализа данных таблицы жизни.
Хотя в основном предназначены для приложений страхования жизни, таблицы жизни функционируют (lifetableconv, lifetablefit, и lifetablegen могут также использоваться социологами, поведенческими психологами, чиновниками общественного здравоохранения и медицинскими исследователями.
Таблицы жизненного цикла основаны на функциях опасности и функциях выживания, которые, в свою очередь, получены из распределения вероятностей. В частности, при непрерывном распределении вероятности его кумулятивная функция распределения равна F (x), а функция плотности вероятности равна f (x) = d F (x )/dx.
Для анализа смертности случайной переменной интереса X является распределение возрастов, в которых люди умирают в популяции. Итак, вероятность того, что кто-то умрет по возрасту x
)
Функция выживания, (s (x)), которая характеризует вероятность того, что человек живет после определенного возраста x >0является
= 1 − F (x)
Для непрерывного распределения вероятности функция опасности является функцией функции выживания с
(x)) dx
и функции выживания являются функцией функции опасности с
(
Модели таблиц жизненного цикла обычно определяют либо функцию опасности, либо функцию выживания. Однако таблицы жизненного цикла являются дискретными и работают с дискретными версиями функций опасности и выживания. Три ряда используются для таблиц жизни, а обозначение является условным. Дискретная функция опасности обозначается как
+ 1) s (x)
которая является вероятностью того, что человек в возрасте x умрет по возрасту x + 1 (где x - в годах). Дискретная функция выживания представлена в терминах начального числа выживших при рождении, называемого таблицей жизни radix (которая обычно составляет 100 000 человек) и обозначается как
(x)
с radix l0 = 100000. Это число, lx, представляет количество людей из 100 000 при рождении, которые все еще живы в возрасте x.
Третья серия связана с функцией плотности вероятности, которая представляет собой число «стандартизированных» смертей в данном году, обозначенное как
lx + 1
На основании нескольких дополнительных правил, касающихся инициализации и завершения этих серий, любая одна серия может быть получена из любой из других серий.
lifetableconv | lifetablefit | lifetablegen