Числа с фиксированной точкой ограничены тем, что они не могут одновременно представлять очень большие или очень маленькие числа, используя разумный размер слова. Это ограничение можно преодолеть, используя научную нотацию. С помощью научной нотации можно динамически размещать бинарную точку в удобном месте и использовать мощности бинарного для отслеживания этого места. Таким образом, можно представить диапазон очень больших и очень малых чисел с несколькими цифрами.
Можно представить любое двоичное число с плавающей запятой в виде научной записи как f2e, где f - дробь (или мантисса), 2 является радиксом или основанием (в данном случае двоичным), а e - экспонентой радикса. Радикс всегда является положительным числом, в то время как f и e могут быть положительными или отрицательными.
При выполнении арифметических операций аппаратные средства с плавающей запятой должны учитывать, что знак, экспонента и дробь кодируются в одном двоичном слове. Это приводит к сложным логическим схемам по сравнению со схемами для двоичных операций с фиксированной точкой.
Программное обеспечение Fixed-Point Designer™ поддерживает числа с плавающей запятой половинной, одинарной и двойной точности в соответствии со стандартом IEEE ® 754.
Существует прямая аналогия между научной нотацией и нотацией точки радикса. Например, научная нотация с использованием пяти десятичных цифр для дроби примет вид
где , 9 и p - целое число неограниченного диапазона.
Запись точки радикса, использующая пять битов для дроби, является одинаковой, за исключением основания числа
где 0,1 и q - целое число неограниченного диапазона.
Для чисел с фиксированной точкой экспонента является фиксированной, но нет причин, по которым двоичная точка должна быть смежной с дробью. Дополнительные сведения см. в разделе Интерпретация двоичных точек.
Стандарт IEEE 754 получил широкое распространение и используется практически со всеми процессорами с плавающей запятой и арифметическими сопроцессорами, за исключением многих процессоров с плавающей запятой DSP.
Этот стандарт задает несколько форматов чисел с плавающей запятой, из которых наиболее широко используются синглы и дубли. Каждый формат содержит три компонента: бит знака, поле дроби и поле экспоненты.
Числа IEEE с плавающей запятой используют представление знака/величины, где бит знака явно включен в слово. Используя представление знака/величины, бит знака 0 представляет положительное число, а бит знака 1 представляет отрицательное число. Это в отличие от представления дополнения двух, предпочтительного для знаковых чисел с фиксированной точкой.
Числа с плавающей запятой могут быть представлены множеством различных способов путем смещения числа влево или вправо от двоичной точки и уменьшения или увеличения степени двоичного числа на соответствующую величину.
Для упрощения операций с числами с плавающей запятой они нормализуются в формате IEEE. Нормализованное двоичное число имеет дробь вида 1.f, где f имеет фиксированный размер для данного типа данных. Поскольку самый левый бит дроби всегда равен 1, нет необходимости хранить этот бит, и поэтому он является неявным (или скрытым). Таким образом, n-битовая дробь хранит n + 1-битовое число. Формат IEEE также поддерживает денормализованные числа, которые имеют долю вида 0.f.
В формате IEEE представления экспоненты смещены. Это означает, что фиксированное значение, смещение, вычитается из поля экспоненты, чтобы получить истинное значение экспоненты. Например, если поле экспоненты равно 8 битам, то представлены числа от 0 до 255, и имеется смещение 127. Обратите внимание, что некоторые значения показателя степени зарезервированы для маркировки Inf (бесконечность), NaN (не-а-число) и денормализованные числа, поэтому истинные значения экспоненты находятся в диапазоне от -126 до 127. Дополнительные сведения см. в разделах Inf и NaN.
Формат с плавающей запятой с двойной точностью IEEE представляет собой 64-битное слово, разделенное на 1-битный знаковый индикатор s, 11-битную смещенную экспоненту e и 52-битную дробь f.

Соотношение между форматом двойной точности и представлением вещественных чисел задается
0исключительное значение в противном случае.,
Дополнительные сведения см. в разделе Исключительная арифметика.
Формат с одинарной точностью IEEE представляет собой 32-битное слово, разделенное на 1-битный знаковый индикатор s, 8-битную смещенную экспоненту e и 23-битную дробь f.
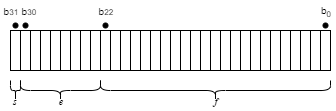
Соотношение между форматом одинарной точности и представлением вещественных чисел задаётся
противном случае исключительное значение.
Дополнительные сведения см. в разделе Исключительная арифметика.
Формат IEEE с полуточностью с плавающей запятой представляет собой 16-битное слово, разделенное на 1-битный знаковый индикатор s, 5-битную смещенную экспоненту e и 10-битную дробь f.
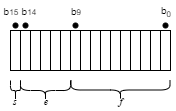
Номера половинной точности поддерживаются в MATLAB ® и Simulink ®. Дополнительные сведения см. в разделеhalf и тип данных полуизмерения в Simulink.
Диапазон числа дает пределы представления. Точность дает расстояние между последовательными числами в представлении. Диапазон и точность числа IEEE с плавающей запятой зависит от конкретного формата.
Диапазон представимых чисел для числа с плавающей запятой IEEE с f-битами, выделенными для дроби, e-битами, выделенными для экспоненты, и смещением e, заданным смещением = 2 (e − 1) − 1, приведен ниже.

где
Нормализованные положительные числа определяются в диапазоне от 2 (1 − смещение) до (2 − 2 − f) 2биас.
Нормализованные отрицательные числа определяются в диапазоне от − 2 (1 − смещение) до − (2 − 2 − f) 2биас.
Положительные числа больше (2 − 2 − f) 2биас и отрицательные числа меньше − (2 − 2 − f) 2биас являются переливами.
Положительные числа меньше 2 (1 − смещение) и отрицательные числа больше − 2 (1 − смещение) являются либо недопотоями, либо денормализованными числами.
Ноль задается специальной битовой комбинацией, где e = 0 и f = 0.
Переливы и недоливы являются результатом исключительных арифметических условий. Числа с плавающей запятой за пределами определенного диапазона всегда отображаются в ±Inf.
Примечание
Можно использовать команды MATLAB realmin и realmax для определения динамического диапазона значений с плавающей запятой двойной точности для компьютера.
Число с плавающей запятой является только аппроксимацией значения «true» из-за конечного размера слова. Поэтому важно иметь понимание точности (или точности) результата с плавающей запятой. Значение v с точностью q задается v ± q. Для чисел IEEE с плавающей запятой
v = (− 1) s (2e-смещение) (1.f)
и
q = 2-f × 2e-смещение
Таким образом, точность связана с количеством битов в поле дроби.
Диапазон, смещение и точность поддерживаемых типов данных с плавающей запятой приведены в таблице ниже.
Тип данных | Нижний предел | Верхний предел | Смещение экспоненты | Точность |
|---|---|---|---|---|
| Половина | 2−14 ≈ 6.1·10−5 | (2−2-10) ·215≈ 6.5·104 | 15 | 2−10 ≈ 10−3 |
Одинок | 2−126 ≈ 10−38 | 2128 ≈ 3 · 1038 | 127 | 2−23 ≈ 10−7 |
Дважды | 2−1022 ≈ 2 · 10−308 | 21024 ≈ 2 · 10308 | 1023 | 2−52 ≈ 10−16 |
Поскольку числа с плавающей запятой представлены с помощью знака/величины, существует два представления нуля, одно положительное и одно отрицательное. Для обоих представлений e = 0 и f.0 = 0.0.
Стандарт IEEE 754 определяет методы и процедуры, позволяющие получать предсказуемые результаты независимо от аппаратной платформы. Денормализованные числа, Inf, и NaN определяются для работы с исключительной арифметикой (недолив и переполнение).
Если неполный поток или переполнение обрабатывается как Inf или NaN, то для устранения этого исключения требуются значительные затраты процессора. Несмотря на то, что стандарт IEEE 754 определяет практику и процедуры для последовательного решения исключительных арифметических условий, изготовители микропроцессоров могут обрабатывать эти условия таким образом, чтобы это не соответствовало стандарту.
Денормализованные числа используются для обработки случаев неполного потока экспоненты. Когда экспонента результата слишком мала (т.е. отрицательная экспонента со слишком большой величиной), результат денормализируется смещением вправо дроби и оставлением экспоненты на ее минимальном значении. Использование денормализованных чисел также называют постепенным понижением расхода. Без денормализованных чисел промежуток между наименьшим представимым ненулевым числом и нулем намного шире, чем промежуток между наименьшим представимым ненулевым числом и следующим большим числом. Постепенный недопоток заполняет этот промежуток и уменьшает влияние экспоненты недопотока до уровня, сравнимого с округлением среди нормализованных чисел. Денормализованные числа обеспечивают расширенный диапазон для малых чисел за счет точности.
Арифметика с участием Inf (бесконечность) рассматривается как ограничивающий случай вещественной арифметики, с бесконечными значениями, определяемыми за пределами диапазона представимых чисел, или −∞ ≤ (представимые числа) < ∞. За исключением особых случаев, обсуждаемых ниже (NaN), любая арифметическая операция, включающая Inf урожаи Inf. Inf представлен наибольшей смещенной экспонентой, допустимой форматом, и долей нуля.
A NaN (not-a-number) - символьная сущность, закодированная в формате с плавающей запятой. Существует два типа NaN: сигнализация и тишина. Передача сигналов NaN сигнализирует о недопустимом исключении операции. Тихое NaN распространяется почти через каждую арифметическую операцию без сигнализации исключения. Следующие операции приводят к NaN: ∞-∞, - ∞+∞, 0×∞, 0/0 и ∞/∞ .
Обе сигнализации NaN и тихо NaN представлены наибольшей смещенной экспонентой, допустимой форматом, и ненулевой дробью. Битовый шаблон для тишины NaN задается как 0,f, где старший бит в f должен быть единицей. Битовый шаблон для сигнализации NaN задается как 0,f, где старший бит в f должен быть нулем, и, по меньшей мере, один из оставшихся битов должен быть ненулевым.