Программное обеспечение Fixed-Point Designer™ помогает разрабатывать и преобразовывать алгоритмы в фиксированные точки. Если вы просто разрабатываете алгоритмы с фиксированной точкой в MATLAB ® или используете Fixed-Point Designer совместно с продуктами для генерации кода MathWorks ®, эти передовые практики помогут вам перейти от общего кода MATLAB к эффективной реализации с фиксированной точкой. Эти передовые практики также рассматриваются на этом веб-семинаре: веб-семинар «Рекомендации по преобразованию фиксированных точек вручную»
Оптимальным способом структурирования кода является отделение основного алгоритма от другого кода, используемого для тестирования и проверки результатов. Создайте тестовый файл для вызова исходного алгоритма MATLAB и версий алгоритма с фиксированной точкой. Например, как показано в следующей таблице, можно настроить некоторые входные данные для подачи в алгоритм, а затем, после обработки этих данных, создать некоторые графики для проверки результатов. Так как вам нужно преобразовать только алгоритмическую часть в фиксированную точку, более эффективно структурировать код так, чтобы у вас был тестовый файл, в котором вы создаете свои входы, вызываете свой алгоритм и строите график результатов, и один (или несколько) алгоритмические файлы, в которых вы делаете основную обработку.
| Исходный код | Передовой опыт | Измененный код |
|---|---|---|
% TEST INPUT
x = randn(100,1);
% ALGORITHM
y = zeros(size(x));
y(1) = x(1);
for n=2:length(x)
y(n)=y(n-1) + x(n);
end
% VERIFY RESULTS
yExpected=cumsum(x);
plot(y-yExpected)
title('Error')
| Проблема Формирование тестового ввода и проверка результатов смешиваются с кодом алгоритма. Зафиксировать Создайте тестовый файл, отдельный от алгоритма. Поместите алгоритм в свою собственную функцию. | Тестовый файл % TEST INPUT
x = randn(100,1);
% ALGORITHM
y = cumulative_sum(x);
% VERIFY RESULTS
yExpected = cumsum(x);
plot(y-yExpected)
title('Error')
Алгоритм в собственной функции function y = cumulative_sum(x)
y = zeros(size(x));
y(1) = x(1);
for n=2:length(x)
y(n) = y(n-1) + x(n);
end
end
|
Тестовый файл можно использовать для:
Перед преобразованием в фиксированную точку убедитесь, что алгоритм с плавающей запятой работает так, как ожидалось. Поведение алгоритма с плавающей запятой - это базовая линия, по которой сравнивается поведение версий алгоритма с фиксированной запятой.
Предлагать типы данных с фиксированной точкой.
Сравните поведение версий алгоритма с фиксированной точкой с базовой линией с плавающей точкой.
Тестовые файлы должны использовать алгоритм в полном рабочем диапазоне, чтобы диапазоны моделирования были точными. Например, для фильтра реалистичными входами являются импульсы, суммы синусоид и чирп-сигналы. С помощью этих входных данных, используя линейную теорию, можно проверить правильность выходных данных. Сигналы, которые обеспечивают максимальный выход, полезны для проверки того, что система не переполняется. Качество предлагаемых типов данных с фиксированной точкой зависит от того, насколько хорошо тестовые файлы охватывают рабочий диапазон алгоритма с требуемой точностью.
С помощью Fixed-Point Designer можно выполнять следующие действия:
Используйте свой код и предоставьте предложения по типу данных, чтобы помочь преобразовать алгоритм в фиксированную точку, используя следующие функции:
buildInstrumentedMex, который генерирует скомпилированный код C, который включает в себя инструментарий регистрации.
showInstrumentationResults, который показывает результаты, зарегистрированные инструментальным, скомпилированным C-кодом.
clearInstrumentationResults, который очищает записанные результаты инструментария из памяти.
Ускорьте алгоритмы с фиксированной точкой, создав файл MEX с помощью fiaccel функция.
Любые алгоритмы MATLAB, которые необходимо измерить с помощью buildInstrumentedMex и любые алгоритмы с фиксированной точкой, которые вы хотите ускорить, используя fiaccel должны соответствовать требованиям и правилам создания кода. Чтобы просмотреть подмножество языка MATLAB, поддерживаемого для генерации кода, см. раздел Функции и объекты, поддерживаемые для генерации кода C/C + +.
Для определения неподдерживаемых функций или конструкций в коде MATLAB используйте один из следующих инструментов.
Добавить %#codegen pragma в верхней части файла MATLAB. Анализатор кода MATLAB помечает функции и конструкции, которые недоступны в подмножестве языка MATLAB, поддерживаемого для генерации кода. Этот совет появляется в режиме реального времени при редактировании кода в редакторе MATLAB.
Дополнительные сведения см. в разделе Проверка кода с помощью анализатора кода MATLAB.
Используйте инструмент «Готовность к созданию кода» для создания статического отчета по коду. Отчет определяет вызовы функций и использование типов данных, которые не поддерживаются для создания кода. Чтобы создать отчет для функции, myFunction1, в командной строке введите coder.screener('myFunction1').
Дополнительные сведения см. в разделе Проверка кода с помощью инструмента готовности к созданию кода.
Перед началом преобразования фиксированной точки определите, какие функции, используемые в алгоритме, не поддерживаются для фиксированной точки. Подумайте, как можно заменить их или иным образом изменить реализацию, чтобы она была более оптимизирована для встроенных целей. Например, может потребоваться найти (или написать собственные) замены для таких функций, как log2, fft, и exp. Другие функции, такие как sin, cos, и sqrt может поддерживать фиксированную точку, но для лучшей эффективности может потребоваться рассмотреть альтернативную реализацию, такую как таблица поиска или алгоритм на основе CORDIC.
Если вы не можете найти замену немедленно, вы можете продолжить преобразование остального алгоритма в фиксированную точку, просто изолируя любые функции, которые не поддерживают фиксированную точку с литьем, чтобы удвоить на входе, и приведение обратно к типу фиксированной точки на выходе.
| Исходный код | Передовой опыт | Измененный код |
|---|---|---|
y = 1/exp(x); | Проблема Зафиксировать Сделайте ввод двойным, пока не появится замена. В этом случае |
y = 1/exp(double(x)); |
Синтаксис (:) = называется подстрочным назначением. При использовании этого синтаксиса MATLAB перезаписывает значение левого аргумента, но сохраняет существующий тип данных и размер массива. Это особенно важно для сохранения фиксированной точки переменных (в отличие от непреднамеренного превращения их в двойные) и для предотвращения роста битов при необходимости сохранения определенного типа данных для вывода.
| Исходный код | Передовой опыт | Измененный код |
|---|---|---|
acc = 0; for n = 1:numel(x) acc = acc + x(n); end | Проблема
Зафиксировать Сохранение исходного типа данных |
acc = 0; for n = 1:numel(x) acc(:) = acc + x(n); end |
Дополнительные сведения см. в разделе Управление ростом битов.
Для создания инструментария и кода создайте функцию точки входа, которая вызывает функцию, которую требуется преобразовать в фиксированную точку. Затем можно привести входные данные функции к различным типам данных. Для сравнения можно добавлять вызовы к различным вариантам функции. Используя функцию начальной точки, можно запускать варианты алгоритма с фиксированной и плавающей точками. Можно также запускать различные варианты фиксированных точек. Этот подход позволяет быстрее выполнять итерацию кода, чтобы получить оптимальный дизайн с фиксированной точкой.
Этот метод преобразования с фиксированной точкой упрощает сравнение нескольких различных реализаций с фиксированной точкой, а также позволяет легко переназначить алгоритм на другое устройство.
Чтобы отделить определения типов данных от алгоритма, выполните следующие действия.
При первом определении переменной используйте cast(x,'like',y) или zeros(m,n,'like',y) для приведения к требуемому типу данных.
Создайте таблицу определений типов данных, начиная с исходных типов данных, используемых в коде. Перед преобразованием в фиксированную точку создайте таблицу типов данных, использующую все отдельные типы данных для поиска несоответствий типов и других проблем.
Запустите код, подключенный к каждой таблице, и просмотрите результаты проверки соединения.
| Исходный код | Передовой опыт | Измененный код |
|---|---|---|
% Algorithm
n = 128;
y = zeros(size(n));
| Проблема Тип данных по умолчанию в MATLAB - плавающая точка с двойной точностью. Зафиксировать
|
% Algorithm T = mytypes('double'); n = cast(128,'like',T.n); y = zeros(size(n),'like',T.y); function T = mytypes(dt)
switch(dt)
case 'double'
T.n = double([]);
T.y = double([]);
case 'single'
T.n = single([]);
T.y = single([]);
end
end |
Отделение спецификаций типов данных от кода алгоритма позволяет:
Повторно используйте код алгоритма с различными типами данных.
Храните свой алгоритм незаполненным спецификациями типов данных и инструкциями switch для различных типов данных.
Улучшите удобочитаемость кода алгоритма.
Переключение между типами данных с фиксированной и плавающей точками для сравнения базовых линий.
Переключение между вариантами настроек фиксированной точки без изменения кода алгоритма.
Перед началом преобразования рассмотрите цели преобразования в фиксированную точку. Вы реализуете свой алгоритм в C или HDL? Каковы ваши целевые ограничения? Ответы на эти вопросы определяют множество свойств фиксированной точки, таких как доступная длина слова, длина дроби и математические режимы, а также доступные математические библиотеки.
Создайте и запустите инструментальную функцию MEX для получения предложений по типам фиксированных точек с помощью buildInstrumentedMex и showInstrumentationResults функции. Тестовые файлы должны использовать ваш алгоритм в полном рабочем диапазоне. Качество предлагаемых типов данных с фиксированной точкой зависит от того, насколько хорошо тестовый файл охватывает рабочий диапазон алгоритма с требуемой точностью. Простой набор тестовых векторов может не использовать весь диапазон типов, поэтому используйте предложения в качестве руководства для выбора начального набора типов с фиксированной точкой и используйте ваше лучшее суждение и опыт в корректировке типов. Если индексы цикла используются только в качестве переменных индекса, они автоматически преобразуются в целочисленные типы, поэтому их не нужно явно преобразовывать в фиксированную точку.
| Код алгоритма | Тестовый файл |
|---|---|
function [y,z] = myfilter(b,x,z)
y = zeros(size(x));
for n = 1:length(x)
z(:) = [x(n); z(1:end-1)];
y(n) = b * z;
end
end
|
% Test inputs
b = fir1(11,0.25);
t = linspace(0,10*pi,256)';
x = sin((pi/16)*t.^2); % Linear chirp
z = zeros(size(b'));
% Build
buildInstrumentedMex myfilter ...
-args {b,x,z} -histogram
% Run
[y,z] = myfilter_mex(b,x,z);
% Show
showInstrumentationResults myfilter_mex ...
-defaultDT numerictype(1,16) -proposeFL
|
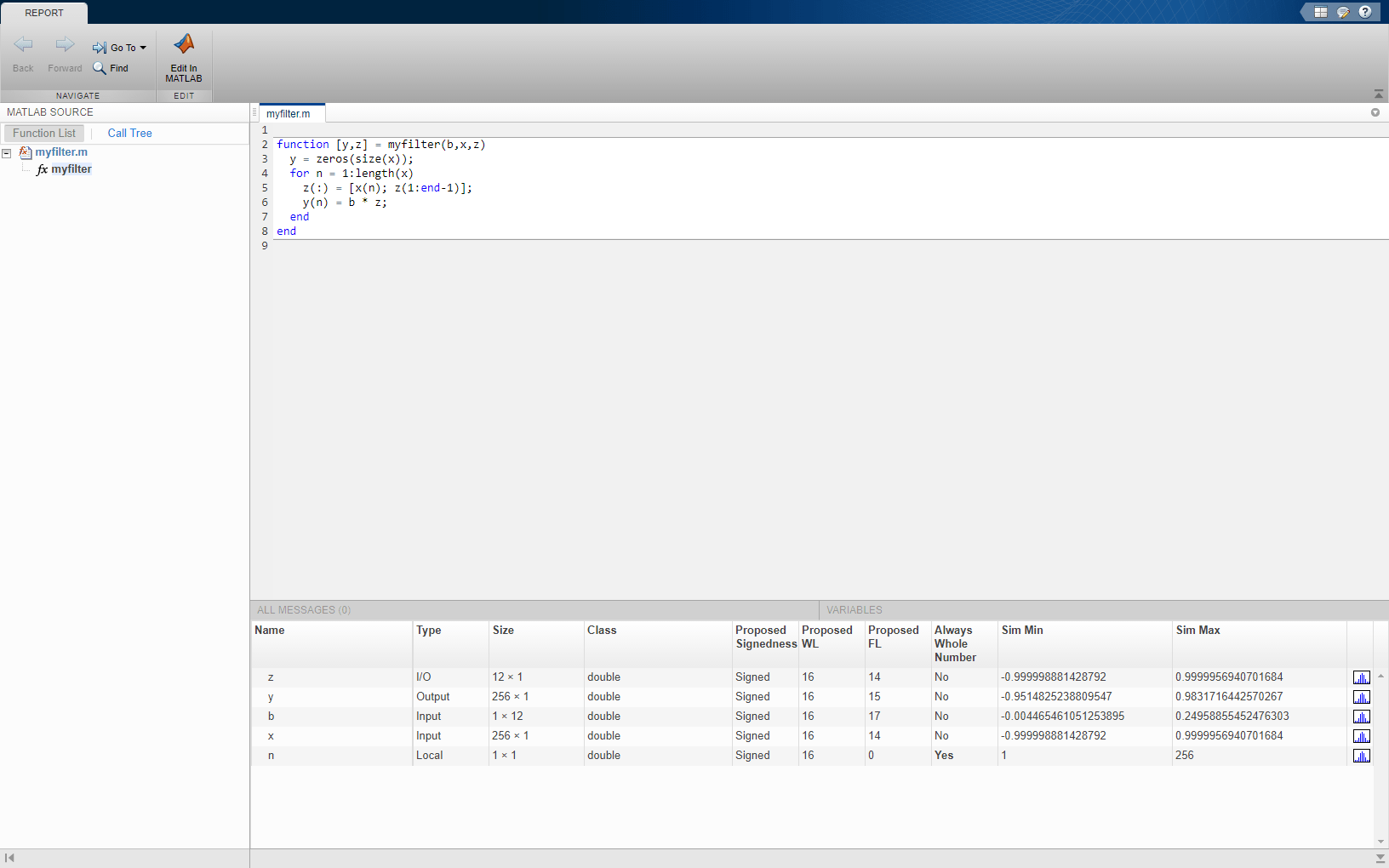
Создайте таблицу типов, используя структуру с прототипами для переменных. Предлагаемые типы вычисляются на основе прогонов моделирования. Долгосрочный прогон моделирования с широким диапазоном ожидаемых данных дает лучшие предложения. Для улучшения предложений можно использовать предлагаемые типы или знание алгоритма и ограничений реализации.
Поскольку используются типы данных, а не значения, укажите значения прототипа как пустые ([]).
В некоторых случаях может оказаться более эффективным оставить некоторые части кода в плавающей точке. Например, когда существует высокий динамический диапазон или эта часть кода чувствительна к ошибкам округления.
| Код алгоритма | Таблицы типов | Тестовый файл |
|---|---|---|
function [y,z]=myfilter(b,x,z,T)
y = zeros(size(x),'like',T.y);
for n = 1:length(x)
z(:) = [x(n); z(1:end-1)];
y(n) = b * z;
end
end
|
function T = mytypes(dt)
switch dt
case 'double'
T.b = double([]);
T.x = double([]);
T.y = double([]);
case 'fixed16'
T.b = fi([],true,16,15);
T.x = fi([],true,16,15);
T.y = fi([],true,16,14);
end
end
|
% Test inputs
b = fir1(11,0.25);
t = linspace(0,10*pi,256)';
x = sin((pi/16)*t.^2);
% Linear chirp
% Cast inputs
T=mytypes('fixed16');
b=cast(b,'like',T.b);
x=cast(x,'like',T.x);
z=zeros(size(b'),'like',T.x);
% Run
[y,z] = myfilter(b,x,z,T);
|
Создайте тестовый файл для проверки того, что алгоритм с плавающей запятой работает так, как ожидалось, перед преобразованием его в фиксированную точку. Можно использовать тот же тестовый файл, чтобы предложить типы данных с фиксированной точкой и сравнить результаты с фиксированной точкой с базовой линией с плавающей точкой после преобразования.
Используйте масштабированные двойники для обнаружения потенциальных переполнений. Масштабированные двойники - это гибрид между числами с плавающей и фиксированной точками. Fixed-Point Designer сохраняет их как двойные с сохранением информации о масштабировании, знаке и длине слова. Для использования масштабированных двойных значений можно использовать свойство переопределения типа данных (DTO) или установить значение 'DataType' свойство для 'ScaledDouble' в fi или numerictype конструктор.
| Кому... | Использовать... | Пример |
|---|---|---|
Локальное переопределение типа данных |
|
T.a = fi([],1,16,13,'DataType', 'ScaledDouble'); a = cast(pi, 'like', T.a) a =
3.1416
DataTypeMode: Scaled double: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 13
|
Глобальное переопределение типа данных |
|
fipref('DataTypeOverride','ScaledDoubles') T.a = fi([],1,16,13); a =
3.1416
DataTypeMode:Scaled double: binary point scaling
Signedness: Signed
WordLength:16
FractionLength:13 |
Дополнительные сведения см. в разделе Масштабированные двойники.
Для точной настройки параметров типа с фиксированной точкой выполните команду buildInstrumentedMex функции с помощью –histogram и затем запустите сгенерированную функцию MEX с требуемыми тестовыми входами. При использовании showInstrumentationResults для отображения отчета о создании кода в отчете отображается значок Гистограмма. Щелкните значок, чтобы открыть элемент NumericTypeScope и просмотреть распределение значений, наблюдаемых в моделировании для выбранной переменной.
Переполнения, указанные красным цветом в отчете о создании кода, отображаются в ячейке «за пределами диапазона» в области NumericTypeScope. Запустите NumericTypeScope для связанной переменной или выражения, щелкнув значок представления гистограммы.![]()
После получения первого набора типов данных с фиксированной точкой в таблицу типов можно добавить различные варианты значений с фиксированной точкой. Можно изменить и выполнить итерацию, чтобы избежать переполнения, скорректировать длины дробей и изменить методы округления, чтобы исключить смещение.
| Код алгоритма | Таблицы типов | Тестовый файл |
|---|---|---|
function [y,z] = myfilter(b,x,z,T) y = zeros(size(x),'like',T.y); for n = 1:length(x) z(:) = [x(n); z(1:end-1)]; y(n) = b * z; end end |
function T = mytypes(dt) switch dt case 'double' T.b = double([]); T.x = double([]); T.y = double([]); case 'fixed8' T.b = fi([],true,8,7); T.x = fi([],true,8,7); T.y = fi([],true,8,6); case 'fixed16' T.b = fi([],true,16,15); T.x = fi([],true,16,15); T.y = fi([],true,16,14); end end |
function mytest % Test inputs b = fir1(11,0.25); t = linspace(0,10*pi,256)'; x = sin((pi/16)*t.^2); % Linear chirp % Run y0 = entrypoint('double',b,x); y8 = entrypoint('fixed8',b,x); y16 = entrypoint('fixed16',b,x); % Plot subplot(3,1,1) plot(t,x,'c',t,y0,'k') legend('Input','Baseline output') title('Baseline') subplot(3,2,3) plot(t,y8,'k') title('8-bit fixed-point output') subplot(3,2,4) plot(t,y0-double(y8),'r') title('8-bit fixed-point error') subplot(3,2,5) plot(t,y16,'k') title('16-bit fixed-point output') xlabel('Time (s)') subplot(3,2,6) plot(t,y0-double(y16),'r') title('16-bit fixed-point error') xlabel('Time (s)') end function [y,z] = entrypoint(dt,b,x) T = mytypes(dt); b = cast(b,'like',T.b); x = cast(x,'like',T.x); z = zeros(size(b'),'like',T.x); [y,z] = myfilter(b,x,z,T); end |
fimath свойства определяют правила выполнения арифметических операций на fi объекты, включая математику, округление и свойства переполнения. Вы можете использовать fimath
ProductMode и SumMode свойства для сохранения естественных типов данных для C и HDL. KeepLSB установка для ProductMode и SumMode моделирует поведение целочисленных операций на языке Си, в то время как KeepMSB моделирует поведение многих DSP-устройств. Различные методы округления требуют различных количеств кода накладных расходов. Установка RoundingMethod свойство для Floor, что эквивалентно усечению двух дополнений, обеспечивает наиболее эффективную реализацию округления. Аналогично, стандартный способ обработки переполнений заключается в переносе с использованием арифметики по модулю. Другие методы обработки переполнения создают дорогостоящую логику. По возможности установите OverflowAction кому Wrap.
| Код MATLAB | Передовой опыт | Сгенерированный код C |
|---|---|---|
% Code being compiled function y = adder(a,b) y = a + b; end With types defined with default fimath settings: T.a = fi([],1,16,0); T.b = fi([],1,16,0); a = cast(0,'like',T.a); b = cast(0,'like',T.b); | Проблема Для реализации переполнения насыщения, ближайшего округления и арифметики полной точности генерируется дополнительный код. |
int adder(short a, short b)
{
int y;
int i;
int i1;
int i2;
int i3;
i = a;
i1 = b;
if ((i & 65536) != 0) {
i2 = i | -65536;
} else {
i2 = i & 65535;
}
if ((i1 & 65536) != 0) {
i3 = i1 | -65536;
} else {
i3 = i1 & 65535;
}
i = i2 + i3;
if ((i & 65536) != 0) {
y = i | -65536;
} else {
y = i & 65535;
}
return y;
}
|
Компилируемый код function y = adder(a,b) y = a + b; end С типами, определенными с настройками fimath, соответствующими типам процессоров: F = fimath(... 'RoundingMethod','Floor', ... 'OverflowAction','Wrap', ... 'ProductMode','KeepLSB', ... 'ProductWordLength',32, ... 'SumMode','KeepLSB', ... 'SumWordLength',32); T.a = fi([],1,16,0,F); T.b = fi([],1,16,0,F); a = cast(0,'like',T.a); b = cast(0,'like',T.b); | Зафиксировать Чтобы повысить эффективность создаваемого кода, выберите математические параметры с фиксированной точкой, соответствующие типам процессоров. |
int adder(short a, short b)
{
return a + b;
}
|
Некоторые встроенные функции MATLAB могут быть более эффективными для реализации с фиксированной точкой. Например, встроенную функцию можно заменить реализацией таблицы Lookup или реализацией CORDIC, которая требует только итеративных операций shift-add.
Часто разделение не полностью поддерживается аппаратными средствами и может привести к медленной обработке. Если алгоритм требует деления, попробуйте заменить его одним из следующих вариантов:
Используйте битовый сдвиг, когда знаменатель является степенью два. Например, bitsra(x,3) вместо x/8.
Умножайте на обратное, когда знаменатель постоянен. Например, x*0.2 вместо x/5.
Для повышения эффективности кода исключите переменные с плавающей запятой. Единственным исключением являются индексы цикла, поскольку они обычно становятся целочисленными типами.