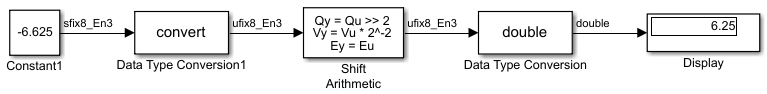Арифметика с фиксированной точкой относится к тому, как обрабатываются подписанные или неподписанные двоичные слова. Простота арифметических функций с фиксированной точкой, таких как сложение и вычитание, обеспечивает экономичную реализацию аппаратных средств.
В следующих разделах описаны правила, которым следует программное обеспечение Simulink ® при выполнении арифметических операций с входами и параметрами. Эти правила организованы в четыре группы на основе задействованных операций: сложение и вычитание, умножение, деление и сдвиги. Для каждой из этих четырех групп правила выполнения указанной операции представлены с примером использования правил.
Архитектура ядра многих процессоров содержит несколько вычислительных блоков, включая арифметические логические блоки (ALU), блоки умножения и накопления (MAC) и переключатели. Эти вычислительные блоки обрабатывают двоичные данные непосредственно и обеспечивают поддержку арифметических вычислений различной точности. АЛУ выполняет стандартный набор арифметических и логических операций, а также разделение. MAC выполняет операции умножения, умножения/сложения и умножения/вычитания. Блок сдвига выполняет логические и арифметические сдвиги, нормализацию, денормализацию и другие операции.
Сложение является наиболее распространенной арифметической операцией, выполняемой процессором. При сложении двух n-разрядных чисел всегда можно получить результат с n + 1 ненулевыми цифрами из-за переноса из самой левой цифры. Для дополнения двух чисел существует три случая:
Если оба числа положительны и результат их сложения имеет знаковый бит 1, то произошло переполнение; в противном случае результат верен.
Если оба числа отрицательные и знак результата равен 0, то произошло переполнение; в противном случае результат верен.
Если числа отличаются от знака, переполнение не может произойти, и результат всегда верен.
Рассмотрим суммирование двух чисел. В идеале, реальные значения подчиняются уравнению
± Vc,
где Vb и Vc - входные значения, а Va - выходные значения. Чтобы увидеть, как на самом деле реализуется суммирование, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в Scaling:
Bi.
Уравнение в дополнении дает решение результирующего уравнения для запомненного целого числа, Qa. Используя сокращенную нотацию, это уравнение становится
EaQc + Bnet,
где FSB и Fsc - скорректированные дробные наклоны, а Bnet - чистый уклон. Оффлайн-преобразования и онлайн-преобразования и операции рассматриваются ниже.
Автономные преобразования. FSB, Fsc и Bnet вычисляются в автономном режиме с использованием округления до ближайшего и насыщения. Кроме того, Bnet сохраняется с использованием типа выходных данных.
Онлайн-конверсии и операции. Остальные операции выполняются процессором с фиксированной точкой в оперативном режиме и зависят от наклонов и смещений для типов входных и выходных данных. Наихудший (самый неэффективный) случай возникает при несовпадении уклонов и смещений. Преобразования и операции в наихудшем случае определяются следующими шагами:
Начальное значение для Qa задается чистым смещением, Bnet:
Bnet.
Первое входное целое значение, Qb, умножается на скорректированный наклон, Fsf:
Предыдущее произведение преобразуется в измененный тип выходных данных, где наклон равен единице, а смещение равно нулю:
QRawProduct).
Это преобразование включает в себя любое необходимое смещение битов, округление или обработку переполнения.
Операция суммирования выполняется:
QTemp.
Это суммирование включает в себя любую необходимую обработку переполнения.
Этапы 2-4 повторяются для каждого суммируемого числа.
Важно отметить, что смещение битов, округление и обработка переполнения применяются к промежуточным этапам (3 и 4), а не к общей сумме.
Дополнительные сведения см. в разделе Процесс суммирования.
Если масштабирование входного и выходного сигналов согласовано, количество операций суммирования уменьшается по сравнению с наихудшим (наиболее неэффективным) случаем. Например, когда входной сигнал имеет тот же дробный наклон, что и выходной сигнал, шаг 2 сводится к умножению на единицу и может быть исключен. Тривиальные шаги в процессе суммирования исключаются как для моделирования, так и для генерации кода. Исключительное использование бинарного масштабирования только для входных сигналов и выходных сигналов является обычным способом устранения несовпадающих наклонов и смещений и приводит к наиболее эффективному моделированию и генерируемому коду.
Умножение n-разрядного двоичного числа на m-разрядное двоичное число приводит к произведению длиной до m + n битов как для подписанных, так и для неподписанных слов. Большинство процессоров выполняют n-бит на n-битное умножение и получают 2n-битовый результат (двойные биты), предполагая отсутствие условия переполнения.
Рассмотрим умножение двух чисел. В идеале, реальные значения подчиняются уравнению
VbVc.
где Vb и Vc - входные значения, а Va - выходные значения. Чтобы увидеть, как на самом деле реализуется умножение, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в Scaling:
Bi.
Решение результирующего уравнения для запомненного на выходе целого числа Qa приведено ниже:
+ BbBc − BaFa2 − Ea.
Умножение с ненулевыми смещениями и несовпадением дробных откосов. Наихудший случай реализации вышеуказанного уравнения происходит, когда наклоны и смещения входного и выходного сигналов не совпадают. В таких случаях для выполнения высокоуровневого умножения (или деления) требуется несколько низкоуровневых целочисленных операций. Выбор реализации этих низкоуровневых вычислений может повлиять на эффективность вычислений, ошибки округления и переполнение.
В блоках Simulink фактическое умножение или операция деления всегда выполняются для переменных с фиксированной точкой, которые имеют нулевые смещения. Если входной сигнал имеет ненулевое смещение, он преобразуется в представление, которое перед операцией масштабируется только в двоичной точке. Если результат должен иметь ненулевое смещение, сначала выполняется операция с временными переменными, имеющими масштабирование только в двоичной точке. Затем результат преобразуется в тип данных и масштабирование конечного вывода.
Если оба входа и выход имеют ненулевые смещения, то операция разбивается следующим образом:
где
Эти уравнения показывают, что временные переменные имеют двоичное масштабирование только для точки. Тем не менее, уравнения не указывают на заметность, длину слова или значения фиксированной степени этих переменных. Программа Simulink присваивает эти свойства временным переменным на основе следующих целей:
Представление исходного значения без переполнения.
Тип данных и масштаб исходного значения определяют максимальное и минимальное реальное значение:
+ B,
+ B.
Тип данных и масштаб временного значения должны быть способны представлять этот диапазон без переполнения. Потеря точности возможна, но переполнение не допускается.
Используйте тип данных, который приводит к эффективным операциям.
Эта цель относится к цели, которая будет использоваться для производственного развертывания проекта. Например, предположим, что проект будет реализован на 16-разрядном процессоре с фиксированной точкой, который обеспечивает 32-разрядный long, 16-битный int, и 8-битный short или char. Для такой цели сохранение эффективности означает, что используется не более 32 бит, а меньшие размеры 8 или 16 бит используются, если они достаточны для поддержания точности.
Поддерживать точность.
В идеале все возможные значения, определенные исходным типом данных и масштабированием, в совершенстве представлены временной переменной. Однако это может потребовать больше битов, чем эффективно. Биты отбрасываются, что приводит к потере точности, в той степени, в какой это требуется для сохранения эффективности.
Например, рассмотрим следующее, предполагая 16-битную цель микропроцессора:
43,25,
где QOriginal - 8-битный неподписанный тип данных. Для этого типа данных:
= 0,
так
43,25.
Минимально возможное значение является отрицательным, поэтому временная переменная должна быть целочисленным типом данных со знаком. Исходная переменная имеет наклон 1, но смещение выражается с большей точностью двумя цифрами после двоичной точки. Чтобы получить полную точность, фиксированная степень временной переменной должна быть -2 или меньше. Программное обеспечение Simulink выбирает минимально возможную точность, которая обычно является наиболее эффективной, если не возникают проблемы переполнения. При масштабировании 2-2 выбор подписанного 16-разрядного или подписанного 32-разрядного кода позволяет избежать переполнения. Для эффективности программное обеспечение Simulink выбирает меньший выбор из 16 бит. Если исходная переменная является входной, то уравнения для преобразования во временную переменную:
173.
Умножение с нулевыми смещениями и несовпадением дробных откосов. Когда смещения равны нулю и дробные откосы не совпадают, реализация сводится к
EaQbQc.
Количество
FbFcFa
рассчитывается в автономном режиме с использованием округления до ближайшего и насыщения. FNet хранится с использованием фиксированного типа данных формы
где ENet и QNet выбираются автоматически для наилучшего представления FNet.
Умножают целые значения Qb и Qc:
QbQc.
Для поддержания полной точности произведения двоичная точка QRawProduct задается суммой двоичных точек Qb и Qc.
Предыдущий продукт преобразуется в тип выходных данных:
QRawProduct).
Это преобразование включает в себя любое необходимое смещение битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Умножение
QTempQNet
выполняется.
Предыдущий продукт преобразуется в тип выходных данных:
Q2RawProduct).
Это преобразование включает в себя любое необходимое смещение битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Этапы 1-4 повторяются для каждого дополнительного числа, которое должно быть умножено.
Умножение с нулевыми смещениями и совпадением дробных откосов. Когда смещения равны нулю, а дробные наклоны совпадают, реализация сводится к
EaQbQc.
Автономные преобразования не выполняются.
Умножают целые значения Qb и Qc:
QbQc.
Для поддержания полной точности произведения двоичная точка QRawProduct задается суммой двоичных точек Qb и Qc.
Предыдущий продукт преобразуется в тип выходных данных:
QRawProduct).
Это преобразование включает в себя любое необходимое смещение битов, округление или обработку переполнения. Преобразования сигналов обсуждают преобразования.
Этапы 1 и 2 повторяются для каждого дополнительного числа, которое должно быть умножено.
Дополнительные сведения см. в разделе Процесс умножения.
В этом разделе рассматривается разделение величин с нулевым смещением.
Примечание
Если любой вход в расчет деления имеет ненулевое смещение, выполняемые операции точно совпадают с операциями умножения, описанными в разделе Умножение с ненулевыми смещениями и несовпадением дробных откосов.
Рассмотрим деление двух чисел. В идеале, реальные значения подчиняются уравнению
Vb/Vc,
где Vb и Vc - входные значения, а Va - выходные значения. Чтобы увидеть, как на самом деле реализуется деление, три идеальных значения должны быть заменены общей схемой кодирования [Slope Bias], описанной в разделе Масштабирование:
Bi.
Для случая, когда коэффициенты регулировки наклона равны единице, а смещения равны нулю для всех сигналов, решение результирующего уравнения для запомненного на выходе целого числа Qa задается следующим уравнением:
Qb/Qc).
Это уравнение включает целочисленное деление и некоторые битовые сдвиги. Если Ea > Eb-Ec, то любые битовые сдвиги идут вправо, и реализация проста. Однако, если Ea < Eb-Ec, то битовые сдвиги находятся влево, и реализация может быть более сложной. Основная проблема заключается в том, что выход имеет большую точность, чем целочисленное деление обеспечивает. Для получения полной точности необходимо дробное деление. Язык программирования C обеспечивает доступ к целочисленному делению только для типов данных с фиксированной точкой. В зависимости от размера числителя можно получить некоторые дробные биты, выполнив сдвиг перед целочисленным делением. В худшем случае может возникнуть необходимость в повторных вычитаниях в программном обеспечении.
В целом, разделение значений - это операция, которую следует избегать во встроенных системах с фиксированной точкой. Деление, в котором выходной сигнал имеет большую точность, чем целочисленное деление (т.е. Ea < Eb-Ec), должно использоваться с еще большим нежеланием.
Дополнительные сведения см. в разделе Процесс разделения.
Почти все микропроцессоры и цифровые сигнальные процессоры поддерживают четко определенные операции сдвига битов (или просто сдвига) для целых чисел. Например, рассмотрим 8-битное целое число без знака 00110101. Результаты 2-разрядного сдвига влево и 2-разрядного сдвига вправо показаны в следующей таблице.
| Операция смены | Двоичное значение | Десятичное значение |
|---|---|---|
Без смены (исходный номер) | 00110101 | 53 |
Сдвиг влево на 2 бита | 11010100 | 212 |
Сдвиг вправо на 2 бита | 00001101 | 13 |
Сдвиг можно выполнить с помощью блока Simulink Shift Arithmetic. Используйте этот блок для выполнения битового сдвига, двоичного точечного сдвига или обоих
Особый случай смещения битов вправо требует рассмотрения обработки самого левого бита, который может содержать информацию знака. Сдвиг вправо можно классифицировать как логический сдвиг вправо или арифметический сдвиг вправо. Для логического сдвига вправо 0 включается в старший бит для каждого битового сдвига. Для арифметического сдвига вправо самый старший бит повторно используется для каждого сдвига битов.
Арифметический блок сдвига выполняет арифметический сдвиг вправо и, следовательно, повторно использует старший бит для каждого битового сдвига вправо. Например, учитывая фиксированную точку номер 11001.011 (-6.625), немного изменения два места направо с запятой в двоичном числе неперемещенные урожаи номер 11110.010 (-1.75), как показано в модели ниже:

Чтобы выполнить логический сдвиг справа от подписанного числа с помощью арифметического блока Shift, используйте блок преобразования типа данных, чтобы привести число как беззнаковое число эквивалентной длины и масштаба. Эта модель показывает, что подписанный номер с фиксированной точкой 11001.001 (-6.625) становится 00110.010 (6.25).