По мере увеличения числа входов в нечеткую систему количество правил увеличивается в геометрической прогрессии. Эта большая база правил снижает вычислительную эффективность нечеткой системы. Это также затрудняет работу нечеткой системы и затрудняет настройку параметров правил и функций членства. Поскольку многие приложения имеют ограниченный объем обучающих данных, большая база правил снижает обобщаемость настроенных нечетких систем.
Для решения этой проблемы можно внедрить систему нечеткого вывода (FIS) в виде дерева более мелких взаимосвязанных объектов FIS, а не в виде одного монолитного объекта FIS. Эти нечеткие деревья также известны как иерархические нечеткие системы, поскольку нечеткие системы расположены в иерархических древовидных структурах. В древовидной структуре выходные сигналы низкоуровневых нечетких систем используются в качестве входных сигналов высокоуровневых нечетких систем. Нечеткое дерево является более эффективным в вычислительном отношении и проще для понимания, чем одна FIS с таким же количеством входов.
Существует несколько нечетких структур дерева, которые можно использовать для приложения. На следующем рисунке показаны обычно используемые нечеткие древовидные структуры: инкрементная, агрегированная или каскадная структура.
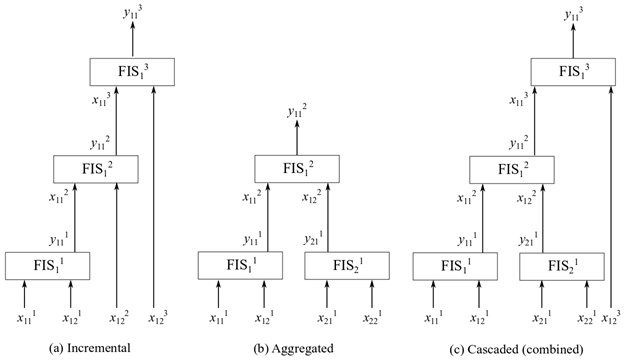
В инкрементной структуре входные значения включаются в несколько этапов для уточнения выходных значений на нескольких уровнях. Например, на предыдущем рисунке показано трехуровневое инкрементное нечеткое дерево, имеющее нечеткие системы вывода , где i указывает индекс FIS на n-м уровне. В инкрементном нечетком дереве i = 1, что означает, что каждый уровень имеет только одну систему нечеткого вывода. На предыдущем рисунке j-й вход i-го FIS на n-м уровне показан как входной , тогда как k-й выход i-го FIS на n-м уровне показан как входной . На рисунке n = 3, j = 1 или 2 и k = 1. Если каждый вход имеет m функций членства (MF), каждый FIS имеет полный набор правил м2. Следовательно, общее число правил nm2 = 3 ⨉ 32 = 27.
На следующем рисунке показана монолитная (n = 1) FIS с четырьмя входами (j = 1, 2, 3, 4) и тремя MF (m = 3 ).
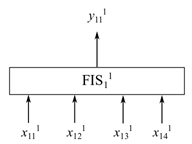
В FIS этой цифры общее количество правил nm4 = 1 ⨉ 34 = 81. Следовательно, общее число правил в инкрементном нечетком дереве является линейным с числом входных пар.
Выбор входных данных на различных уровнях в инкрементном нечетком дереве использует входные ранги на основе их вклада в конечные выходные значения. Входные значения, которые вносят наибольший вклад, обычно используются на самом низком уровне, в то время как наименее влиятельные - на самом высоком уровне. Другими словами, входные значения низкого ранга зависят от входных значений высокого ранга.
В инкрементном нечетком дереве каждое входное значение обычно вносит определенный вклад в процесс вывода без существенной корреляции с другими входными данными. Например, нечеткая система прогнозирует возможность покупки автомобиля, используя четыре входа: цвет, количество дверей, мощность лошади и автопилот. Входными данными являются четыре отличительных особенности автомобиля, которые могут независимо влиять на решение покупателя. Следовательно, входные данные могут быть ранжированы с использованием существующих данных для построения нечеткого дерева, как показано на следующем рисунке.
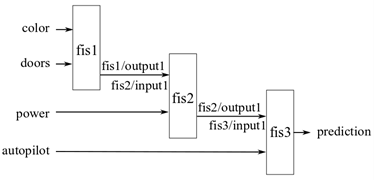
Пример, иллюстрирующий создание инкрементного нечеткого дерева в MATLAB ®, см. в примере «Создание инкрементного дерева FIS» на fistree справочная страница.
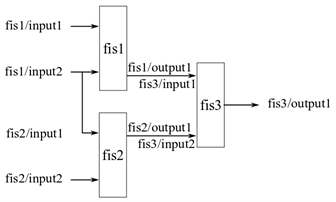
В агрегированной структуре входные значения включаются в виде групп на самом низком уровне, где каждая входная группа подается в FIS. Выходы нечетких систем более низкого уровня объединяются (агрегируются) с использованием нечетких систем более высокого уровня. Например, ниже показано двухуровневое агрегированное нечеткое дерево, имеющее системы нечеткого вывода , где в обозначает индекс FIS на n-м уровне.
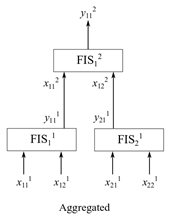
В этом агрегированном нечетком дереве i1 = 1,2 и i2 = 1. Следовательно, каждый уровень включает в себя различное количество FIS. j-й вход внутреннего FIS показан на рисунке как входной , а k-й выход внутреннего FIS показан как выходной . На рисунке j = 1,2 и k = 1. Другими словами, каждый FIS имеет два входа и один выход. Если каждый вход имеет m MF, то каждый FIS имеет полный набор правил м2. Следовательно, общее количество правил для трех нечетких систем составляет 3 м2 = 3 ⨉ 32 = 27, что является тем же самым, что и инкрементная FIS для аналогичной конфигурации.
В агрегированном нечетком дереве входные значения, естественно, группируются вместе для принятия конкретных решений. Например, задача автономной навигации робота сочетает в себе предотвращение препятствий и достижение цели подзадачи для навигации без столкновений. Для выполнения задачи навигации нечеткое дерево может использовать четыре входа: расстояние до ближайшего препятствия, угол ближайшего препятствия, расстояние до цели и угол цели. Измеряют расстояния и углы относительно текущего положения и направления курса робота. В этом случае на самом низком уровне входы естественно группируются, как показано на следующем рисунке: расстояние препятствия и угол препятствия (группа 1) и целевое расстояние и целевой угол (группа 2). Две нечеткие системы по отдельности обрабатывают индивидуальные групповые входы, а затем другая нечеткая система объединяет их выходы, чтобы создать курс без столкновений для робота.
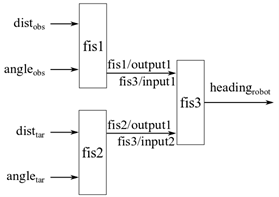
Пример, иллюстрирующий создание агрегированного нечеткого дерева в MATLAB, см. в примере Создание агрегированного дерева FIS на fistree справочная страница.
В варианте агрегированной структуры, известном как параллельная структура
[1], выходы нечетких систем самого низкого уровня непосредственно суммируются для генерации конечного выходного значения. На следующем рисунке показан пример параллельного нечеткого дерева, где выходы fis1 и fis2 суммируют для получения конечного результата.
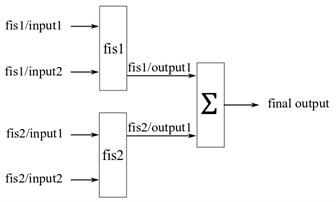
fistree объект не обеспечивает суммирующий узел Λ. Поэтому для вычисления параллельного нечеткого дерева необходимо добавить пользовательский метод агрегации. Пример см. в примере «Создание и оценка параллельного дерева FIS» на fistree справочная страница.
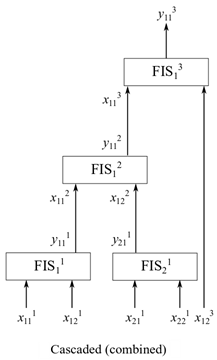
Каскадная структура, также известная как комбинированная структура, объединяет как инкрементные, так и агрегированные структуры для построения нечеткого дерева. Эта структура подходит для системы, которая включает в себя как коррелированные, так и некоррелированные входы. Дерево группирует коррелированные входы в агрегированной структуре и добавляет некоррелированные входы в инкрементную структуру. На следующем рисунке показан пример каскадной древовидной структуры, где первые четыре входа сгруппированы попарно в агрегированной структуре, а пятый вход добавлен в инкрементную структуру.
Например, рассмотрим задачу навигации робота, описанную в агрегированной структуре. Предположим, что эта задача включает в себя другой ввод, предыдущий заголовок робота, учитываемый для предотвращения больших изменений в курсе робота. Этот ввод можно добавить с помощью инкрементной структуры следующей диаграммы.
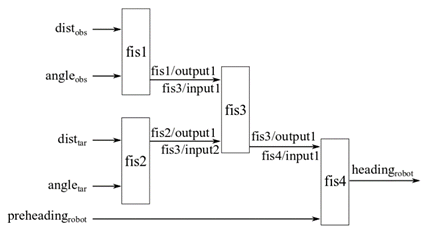
Пример, иллюстрирующий создание агрегированного нечеткого дерева в MATLAB, см. в примере «Создание каскадного дерева FIS» на fistree справочная страница.
При оценке fistree объект возвращает результаты только для открытых выходов, которые не подключены ни к каким входам FIS в нечетком дереве. При необходимости можно получить доступ к другим выводам в дереве. Например, на следующей диаграмме агрегированного нечеткого дерева можно получить выходные данные fis2 при вычислении дерева.
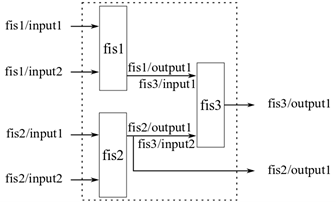
Можно добавить такие выходные данные в fistree объект. Можно также удалить выходные данные при условии, что нечеткое дерево всегда имеет хотя бы один выходной сигнал. Пример см. в разделе «Обновление выходных данных дерева FIS» на fistree справочная страница.
A fistree объект позволяет использовать одно и то же значение для нескольких входов. Например, на следующем рисунке: input2 из fis1 и input1 из fis2 использовать одно и то же значение во время анализа.
Пример, показывающий, как таким образом построить дерево FIS, см. в примере «Использовать одно и то же значение для нескольких входов дерева FIS» на fistree справочная страница.
Можно добавить или удалить отдельные элементы FIS из fistree объект. При этом программное обеспечение автоматически обновляет Connections, Inputs, и Outputs свойства fistree объект. Пример см. в примере «Обновление нечетких систем вывода в дереве FIS» на fistree справочная страница.
После настройки внутренних соединений в нечетком дереве следующим шагом будет настройка параметров дерева. Пример см. в разделе Настройка дерева FIS для прогнозирования пробега газа.
[1] Сиддик, Назмул и Ходжат Адели. Вычислительный интеллект: синергия нечеткой логики, нейронных сетей и эволюционных вычислений. Оксфорд, Великобритания: John Wiley & Sons Ltd, 2013. https://doi.org/10.1002/9781118534823.