В этом примере показано, как найти локальный минимум функции с помощью смоделированного отжига. В примере представлены два подхода к минимизации: работа в командной строке и использование задачи «Оптимизировать интерактивный редактор».
Пятая функция де Йонга - двумерная функция со множеством (25) локальных минимумов. На следующем сюжете неясно, какой из этих локальных минимумов является глобальным минимумом.
dejong5fcn

Многие стандартные алгоритмы оптимизации застревают в локальных минимумах. Поскольку моделируемый алгоритм отжига выполняет широкий случайный поиск, вероятность захвата локального минимума уменьшается.
Примечание.Поскольку при моделировании отжига используются генераторы случайных чисел, каждый раз при запуске этого алгоритма можно получить разные результаты. Дополнительные сведения см. в разделе Воспроизведение результатов.
Чтобы запустить моделируемый алгоритм отжига без ограничений, вызовите simulannealbnd в командной строке с помощью целевой функции в dejong5fcn.m, на который ссылается анонимная функция @dejong5fcn в следующем коде.
rng(10,'twister') % for reproducibility fun = @dejong5fcn; [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-16.1292 -15.8214
fval =
6.9034В результатах:
x - конечная точка, возвращаемая алгоритмом.
fval - значение целевой функции в конечной точке.
Минимизацию также можно выполнить с помощью задачи «Оптимизировать интерактивный редактор», которая обеспечивает визуальный подход.
Создайте новый сценарий в реальном времени, нажав кнопку «Создать сценарий в реальном времени» в разделе «Файл» на вкладке «Главная».
Вставка задачи «Оптимизировать интерактивный редактор». Перейдите на вкладку Вставка, а затем в разделе Код выберите Задача > Оптимизировать.
Для использования при вводе данных о проблемах вставьте новый раздел, нажав кнопку «Разрыв раздела» на вкладке «Вставка». Новые разделы появляются над и под задачей.
В новом разделе над задачей введите следующий код для определения начальной точки и целевой функции.
x0 = [0 0]; fun = @dejong5fcn;
Чтобы поместить эти переменные в рабочее пространство, запустите раздел, нажав клавиши CTRL + ENTER.
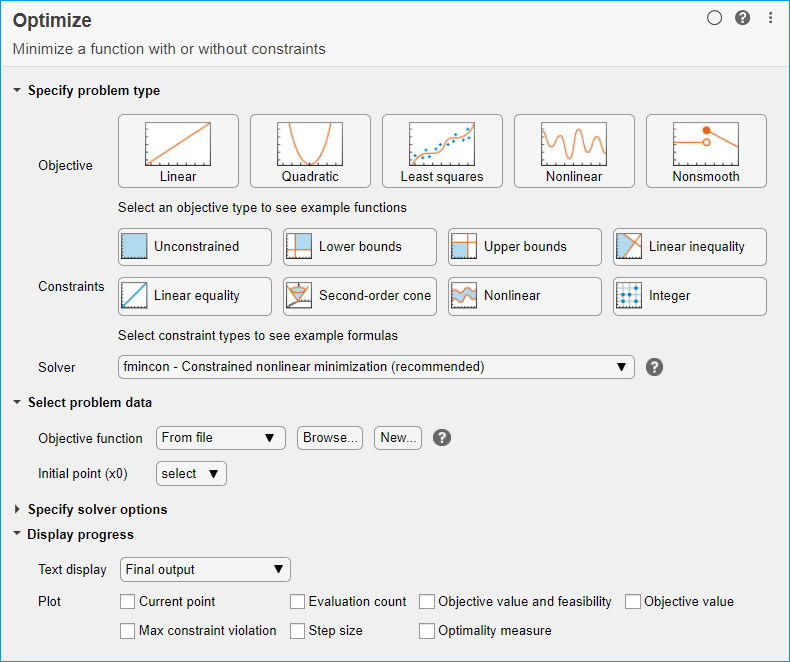
В разделе Задание типа задачи нажмите кнопку Цель > Нелинейный.
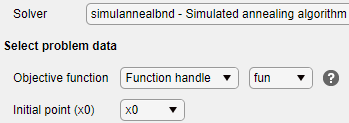
Выберите Решатель > simulannealbnd - Алгоритм имитационного отжига.
В разделе Select problem data задачи выберите Objective function > Function handle, а затем выберите fun.
Выберите Начальная точка (x0) > x0.
В разделе «Отображение хода выполнения» задачи выберите график «Наилучшее значение».
Чтобы запустить решатель, нажмите кнопку опций ⁝ в правом верхнем углу окна задачи и выберите Выполнить раздел. График отображается в отдельном окне рисунка и в области вывода задания. Обратите внимание, что ваш график может отличаться от показанного, потому что simulannealbnd - стохастический алгоритм.
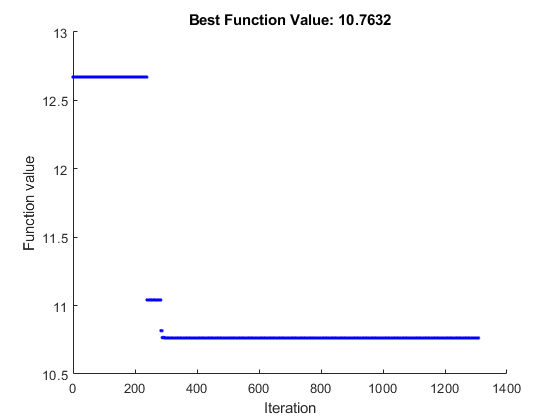
Чтобы увидеть решение и наилучшее значение целевой функции, посмотрите в верхней части задачи.
![]()
Задача «Оптимизировать интерактивный редактор» возвращает переменные с именем solution и objectiveValue в рабочую область.
Чтобы просмотреть значения этих переменных, введите следующий код в разделе под задачей.
disp(solution) disp(objectiveValue)
Запустите раздел, нажав Ctrl + Enter.
disp(solution)
-32.0285 -0.1280
disp(objectiveValue)
10.7632
Задача «Оптимизировать интерактивный редактор» и командная строка позволяют формулировать и решать задачи, и они дают одинаковые результаты. Командная строка является более удобной, но предоставляет меньше возможностей для выбора решателя, настройки проблемы и выбора таких параметров, как функции печати. Можно также запустить проблему с помощью команды Оптимизировать (Optimize), а затем создать код для использования в командной строке, как в разделе Решение ограниченной нелинейной проблемы на основе решателя (Solver-Based).