В качестве примера рассмотрим следующую функцию.
9) 2≤160otherwise.
На следующем рисунке показан график функции.
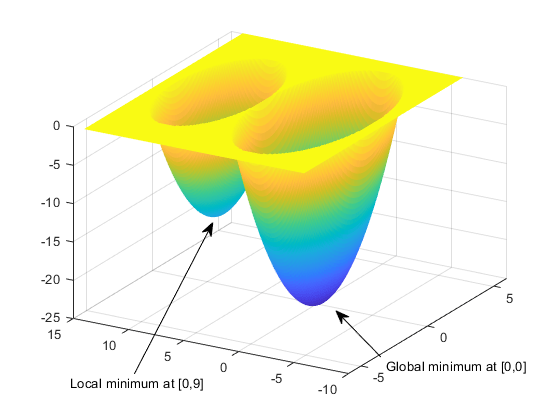
Глобальный минимум функции имеет значение (0, 0), где ее значение равно -25. Однако функция также имеет локальный минимум в (0, 9), где ее значение равно -16.
Чтобы создать файл, вычисляющий функцию, скопируйте и вставьте следующий код в новый файл в редакторе MATLAB ® Editor.
function z = poll_example(x) if x(1)^2 + x(2)^2 <= 25 z = x(1)^2 + x(2)^2 - 25; elseif x(1)^2 + (x(2) - 9)^2 <= 16 z = x(1)^2 + (x(2) - 9)^2 - 16; else z = 0; end
Сохранить файл как poll_example.m в папке на пути MATLAB.
Для выполнения поиска шаблона в функции введите следующее.
options = optimoptions('patternsearch','Display','iter'); [x,fval] = patternsearch(@poll_example,[0,5],... [],[],[],[],[],[],[],options)
MATLAB возвращает таблицу итераций и решение.
x =
0 9
fval =
-16Алгоритм начинается с a = оценки функции в начальной точке, f (0, 5) = 0. Опрос оценивает следующее во время своих первых итераций.
f (0 , 5 ) + (1 , 0)) = f ( 1, 5) = 0
f ((0 , 5 ) + (0 , 1)) = f ( 0, 6) = -7
Как только поиск опрашивает точку сетки (0, 6), в которой значение целевой функции меньше, чем в начальной точке, он прекращает опрос текущей сетки и устанавливает текущую точку в следующей итерации на (0, 6). Следовательно, поиск перемещается к локальному минимуму (0, 9) в первой итерации. Вы видите это, глядя на первые две строки отображения командной строки.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 3 -7 2 Successful PollОбратите внимание, что поиск шаблона выполняет только две оценки целевой функции в первой итерации, увеличивая общее число функций с 1 до 3.
Далее, установить UseCompletePoll кому true и повторно запустите оптимизацию.
options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
[],[],[],[],[],[],[],options);На этот раз поиск шаблона находит глобальный минимум в (0, 0). Отличие этого прогона от предыдущего состоит в том, что UseCompletePoll установить в значение true, при первой итерации поиск массива опрашивает все четыре точки сетки.
f (0 , 5 ) + (1 , 0)) = f ( 1, 5) = 0
f ((0 , 5 ) + (0 , 1)) = f ( 0, 6) = -6
f ((0 , 5 ) + (-1 , 0)) = f (- 1, 5) = 0
f ((0 , 5 ) + (0 , -1)) = f ( 0, 4) = -9
Поскольку последняя точка сети имеет наименьшее значение целевой функции, поиск массива выбирает ее в качестве текущей точки при следующей итерации. Первые две строки экрана командной строки показывают это.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 5 -9 2 Successful PollВ этом случае целевая функция вычисляется четыре раза в первой итерации. В результате поиск шаблона перемещается к глобальному минимуму (0, 0).
На следующем рисунке сравнивается последовательность точек, возвращаемых, если для параметра «Завершить опрос» установлено значение Off с последовательностью, когда Complete poll имеет значение On.
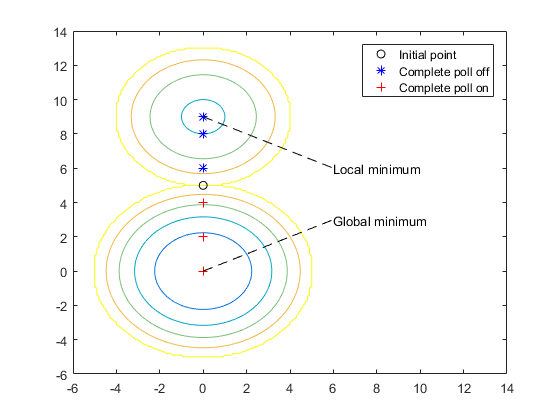
В этом примере показано взаимодействие нескольких опций опроса с точки зрения итераций и суммарных оценок функций. Основные результаты:
GSS эффективнее GPS или MADS для проблем с линейными ограничениями.
Настройка или нет UseCompletePoll кому true повышение эффективности или снижение эффективности неясно, хотя это влияет на количество итераций.
Аналогично, имеет ли 2N опрос более или менее эффективен, чем наличие Np1 опрос также неясен. Самый эффективный опрос - GSS Positive Basis Np1 с полным набором параметров опроса, равным on. Наименее эффективным является MADS Positive Basis Np1 с полным набором параметров опроса, равным on.
Примечание
Эффективность алгоритма зависит от проблемы. GSS эффективен для проблем с линейными ограничениями. Однако прогнозировать последствия для эффективности других вариантов опроса сложно, как и знать, какой тип опроса лучше всего работает с другими ограничениями.
Проблема та же, что и в разделе «Решение с помощью поиска массива» в задаче «Оптимизировать интерактивный редактор». Эта линейно ограниченная проблема использует lincontest7 файл, поставляемый с панелью инструментов:
Введите в рабочую область MATLAB следующее.
x0 = [2 1 0 9 1 0]; Aineq = [-8 7 3 -4 9 0]; bineq = 7; Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3]; beq = [84 62 65 1];
Задайте начальные опции и целевую функцию.
options = optimoptions('patternsearch',... 'PollMethod','GPSPositiveBasis2N',... 'PollOrderAlgorithm','consecutive',... 'UseCompletePoll',false); fun = @lincontest7;
Выполните оптимизацию, присвоив имя output структура outputgps2noff.
[x,fval,exitflag,outputgps2noff] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Задайте параметры для использования полного опроса.
options.UseCompletePoll = true;
Выполните оптимизацию, присвоив имя output структура outputgps2non.
[x,fval,exitflag,outputgps2non] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Продолжайте аналогичным образом создавать структуры вывода для других методов опроса с помощью UseCompletePoll набор true и false: outputgss2noff, outputgss2non, outputgssnp1off, outputgssnp1on, outputmads2noff, outputmads2non, outputmadsnp1off, и outputmadsnp1on.
Имеются результаты 12 прогонов оптимизации. В следующей таблице показана эффективность прогонов, измеренная в общих подсчетах функций и в итерациях. Результаты MADS могут отличаться, так как MADS является стохастическим алгоритмом.
| Алгоритм | Подсчет функций | Повторения |
|---|---|---|
| GPS2N, полный опрос выключен | 1462 | 136 |
| GPS2N, полный опрос на | 1396 | 96 |
| GPSNp1, полный опрос выключен | 864 | 118 |
| GPSNp1, полный опрос на | 1007 | 104 |
| GSS2N, полный опрос выключен | 758 | 84 |
| GSS2N, полный опрос на | 889 | 74 |
| GSSNp1, полный опрос выключен | 533 | 94 |
| GSSNp1, полный опрос на | 491 | 70 |
| MADS2N, полный опрос выключен | 922 | 162 |
| MADS2N, полный опрос на | 2285 | 273 |
| MADSNp1, полный опрос выключен | 1155 | 201 |
| MADSNp1, полный опрос на | 1651 | 201 |
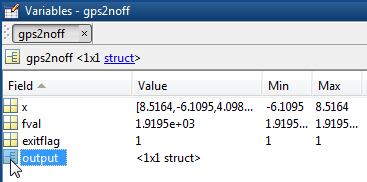
Чтобы получить, например, первую строку в таблице, введите gps2noff.output.funccount и gps2noff.output.iterations. Можно также проверить параметры в редакторе переменных, дважды щелкнув параметры в браузере рабочего пространства, а затем дважды щелкнув значок output структура.
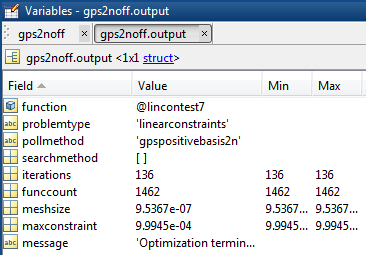
Кроме того, можно получить доступ к данным из структур вывода.
[outputgps2noff.funccount,outputgps2noff.iterations]
ans =
1462 136Основными результатами, полученными из таблицы, являются:
Настройка UseCompletePoll кому true обычно снижает количество итераций для GPS и GSS, но изменение числа оценок функций непредсказуемо.
Настройка UseCompletePoll кому true не обязательно изменяет число итераций для MADS, но существенно увеличивает число оценок функций.
Наиболее эффективные настройки алгоритма/опций с эффективностью, означающей наименьшее количество функций:
'GSSPositiveBasisNp1' с UseCompletePoll установить в значение true (подсчет функций 491)
'GSSPositiveBasisNp1' с UseCompletePoll установить в значение false (подсчет функций 533)
'GSSPositiveBasis2N' с UseCompletePoll установить в значение false (подсчет функций 758)
'GSSPositiveBasis2N' с UseCompletePoll установить в значение true (подсчет функций 889)
Другие методы опроса имели количество функций, превышающее 900.
Для этой проблемы наиболее эффективным является опрос 'GSSPositiveBasisNp1' с UseCompletePoll установить в значение true, хотя UseCompletePoll настройка имеет лишь небольшое отличие. Наименее эффективный опрос 'MADSPositiveBasis2N' с UseCompletePoll установить в значение true. В этом случае UseCompletePoll настройка имеет существенное значение.