Графики частотной характеристики показывают комплексные значения передаточной функции как функцию частоты.
В случае линейных динамических систем передаточная функция G по существу является оператором, который принимает вход u линейной системы на выход y:
Гу
Для системы непрерывного времени передаточная функция связывает преобразования Лапласа входных U (s) и выходных Y (s):
U (s)
В этом случае частотная функция G (iw) является передаточной функцией, оцениваемой на воображаемой оси s = iw.
Для дискретно-временной системы, дискретизированной с временным интервалом Т, передаточная функция связывает Z-преобразования входа U (z) и выхода Y (z):
U (z)
В этом случае частотная функция G (eiwT) является передаточной функцией G (z), оцениваемой на единичной окружности. Аргумент частотной функции G (eiwT) масштабируется временем Т выборки, чтобы сделать частотную функцию периодической с частотой 2πT выборки.
Можно построить график частотной характеристики модели, чтобы получить представление о характеристиках линейной динамики модели, включая частоту пиковой характеристики и пределы устойчивости. Графики частотной характеристики доступны для всех линейных моделей.
Примечание
Графики частотной характеристики недоступны для нелинейных моделей. Кроме того, графики Найквиста не поддерживают модели временных рядов, которые не имеют входных данных.
Частотная характеристика линейной динамической модели описывает реакцию модели на синусоидальные входы. Если вход u (t) является синусоидой определенной частоты, то выход y (t) также является синусоидой той же частоты. Однако величина отклика отличается от величины входного сигнала, и фаза отклика сдвигается относительно входного сигнала.
Графики частотной характеристики дают представление о динамике линейных систем, таких как частотно-зависимые коэффициенты усиления, резонансы и фазовые сдвиги. Графики частотной характеристики также содержат информацию о требованиях контроллера и достижимых полосах пропускания. Наконец, графики частотной характеристики также могут помочь проверить, насколько хорошо линейная параметрическая модель, такая как линейная модель ARX или модель пространства состояний, фиксирует динамику.
Одним из примеров того, как графики частотной характеристики помогают проверить другие модели, является то, что можно оценить частотную характеристику из данных с помощью спектрального анализа (непараметрическая модель), а затем построить график результата спектрального анализа поверх частотной характеристики параметрических моделей. Поскольку непараметрические и параметрические модели получаются с использованием различных алгоритмов, согласование между этими моделями повышает уверенность в результатах параметрической модели.
Приложение System Identification поддерживает следующие типы графиков частотного отклика для линейных параметрических моделей, линейных моделей состояния-пространства и непараметрических моделей частотного отклика:
График моде реакции модели. График Боде состоит из двух графиков. Верхний график показывает величину |, на которую передаточная функция G увеличивает амплитуду синусоидального входа. На нижнем графике показана argG, на которую передаточная функция сдвигает вход. Вход в систему является синусоидой, а выход также является синусоидой с той же частотой.
График модели возмущения, называемый шумовым спектром. Этот график аналогичен графику Боде отклика модели, но он показывает спектр выходной мощности шумовой модели. Дополнительные сведения см. в разделе Графики шумового спектра.
(Только в окне команд MATLAB ®)
Найквистский сюжет. Строит график мнимой и реальной частей передаточной функции.
На следующем рисунке показан образец графика Боде динамики модели, созданной в приложении Идентификация системы.
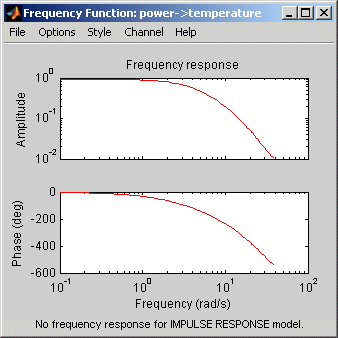
В дополнение к кривой частота-отклик можно отобразить доверительный интервал на графике. Сведения о том, как показать или скрыть доверительный интервал, см. в описании параметров графика в разделе Графики графика с помощью приложения идентификации системы
Доверительный интервал соответствует диапазону значений отклика с определенной вероятностью быть фактическим откликом системы. Инструментарий использует оценочную неопределенность в параметрах модели для вычисления доверительных интервалов и предполагает, что оценки имеют гауссово распределение.
Например, для 95% доверительного интервала область вокруг номинальной кривой представляет диапазон, в котором существует 95% вероятность того, что она содержит истинный отклик системы. Доверительный интервал можно указать как вероятность (между 0 и 1) или как число стандартных отклонений гауссова распределения. Например, вероятность 0,99 (99%) соответствует 2,58 стандартным отклонениям.