Преобразование Фурье является представлением изображения в виде суммы комплексных экспоненций различных величин, частот и фаз. Преобразование Фурье играет решающую роль в широком диапазоне приложений обработки изображений, включая усовершенствование, анализ, восстановление и сжатие.
Если f (m, n) является функцией двух дискретных пространственных переменных m и n, то двумерное преобразование Фурье f (m, n) определяется соотношением
jü 1me − jstart2n.
Переменные start1 и start2 являются частотными переменными; их единицами являются радианы на образец. F (start1, start2) часто называют представлением в частотной области f (m, n). F (start1, start2) - комплекснозначная функция, которая является периодической как в start1, так и в start2, с периодом 2λ. Из-за периодичности обычно отображается только −π≤ω1,ω2≤π диапазона. Заметим, что F (0,0) - это сумма всех значений f (m, n). По этой причине F (0,0) часто называют постоянной составляющей или постоянной составляющей преобразования Фурье. (Постоянный ток означает постоянный ток; это электротехнический термин, который относится к источнику питания постоянного напряжения, в отличие от источника питания, напряжение которого изменяется синусоидально.)
Обратная операция преобразования - это операция, которая при выполнении для преобразованного изображения создает исходное изображение. Обратное двумерное преобразование Фурье задаётся
(,
Грубо говоря, это уравнение означает, что f (m, n) можно представить как сумму бесконечного числа комплексных экспоненциалов (синусоид) с различными частотами. Величина и фаза вклада на частотах (start1, start2) задаются F (start1, start2).
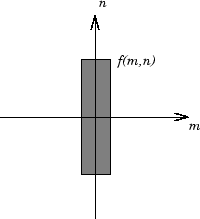
Для иллюстрации рассмотрим функцию f (m, n), которая равна 1 в прямоугольной области и 0 везде. Для упрощения диаграммы f (m, n) показана как непрерывная функция, даже если переменные m и n являются дискретными.
Прямоугольная функция
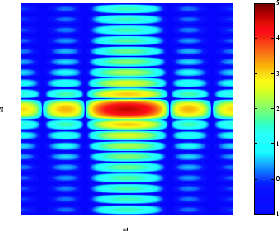
На следующем рисунке в качестве графика сетки показана величина преобразования Фурье,
) |,
прямоугольной функции, показанной на предыдущем рисунке. Сетчатый график величины является обычным способом визуализации преобразования Фурье.
Изображение величины прямоугольной функции

Пик в центре графика равен F (0,0), что является суммой всех значений в f (m, n). На графике также показано, что F (start1, start2) имеет больше энергии на высоких горизонтальных частотах, чем на высоких вертикальных частотах. Это отражает тот факт, что горизонтальные сечения f (m, n) являются узкими импульсами, в то время как вертикальные сечения являются широкими импульсами. Узкие импульсы имеют большее высокочастотное содержание, чем широкие импульсы.
Другим распространенным способом визуализации преобразования Фурье является отображение
) |
в виде изображения, как показано на иллюстрации.
Журнал преобразования Фурье прямоугольной функции
Использование логарифма помогает вывести детали преобразования Фурье в областях, где F (start1, start2) очень близок к 0.
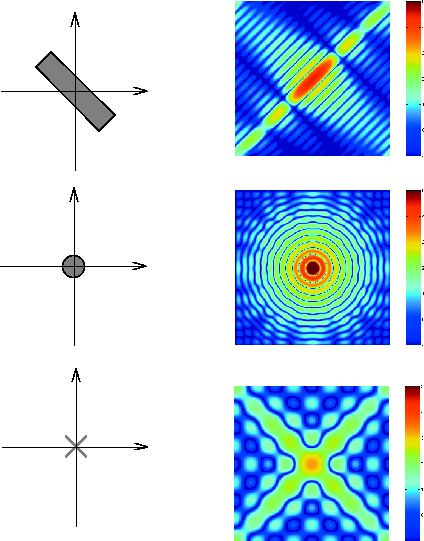
Примеры преобразования Фурье для других простых форм показаны ниже.
Преобразования Фурье некоторых простых форм
Работа с преобразованием Фурье на компьютере обычно включает в себя форму преобразования, известную как дискретное преобразование Фурье (DFT). Дискретное преобразование - это преобразование, входные и выходные значения которого являются дискретными выборками, что делает его удобным для компьютерных манипуляций. Существует две основные причины использования этой формы преобразования:
Вход и выход DFT являются дискретными, что делает его удобным для компьютерных манипуляций.
Существует быстрый алгоритм для вычисления DFT, известный как быстрое преобразование Фурье (FFT).
ДПФ обычно определяется для дискретной функции f (m, n), которая ненулевая только над конечной 0≤m≤M−1 0≤n≤N−1. Двумерные отношения M-на-N DFT и обратные отношения M-на-N DFT задаются
, 1,..., N − 1
и
..., N − 1
Значения F (p, q) являются коэффициентами DFT f (m, n). Нулевой частотный коэффициент F (0,0) часто называют «постоянной составляющей». DC - электротехнический термин, обозначающий постоянный ток. (Обратите внимание, что индексы матрицы в MATLAB ® всегда начинаются с 1, а не 0; поэтому матричные элементы f (1,1) и F (1,1) соответствуют математическим величинам f (0,0) и F (0,0) соответственно.)
Функции MATLAB fft, fft2, и fftn реализовать алгоритм быстрого преобразования Фурье для вычисления одномерного DFT, двухмерного DFT и N-мерного DFT соответственно. Функции ifft, ifft2, и ifftn вычислить обратный DFT.
Коэффициенты ДПФ F (p, q) являются выборками преобразования Фурье F (start1, start2).
− 1q = 0,1,..., N − 1
Построение матрицы f это аналогично функции f (m, n) в примере определения преобразования Фурье. Помните, что f (m, n) равно 1 в прямоугольной области и 0 в другом месте. Используйте двоичное изображение для представления f (m, n).
f = zeros(30,30); f(5:24,13:17) = 1; imshow(f,'InitialMagnification','fit')
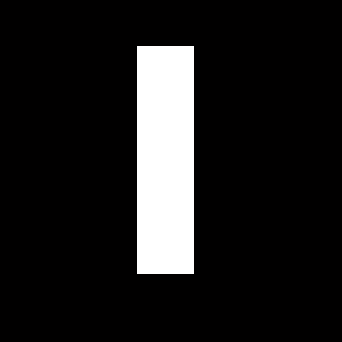
Вычислите и визуализируйте DFT 30 на 30 f с помощью этих команд.
F = fft2(f); F2 = log(abs(F)); imshow(F2,[-1 5],'InitialMagnification','fit'); colormap(jet); colorbar
Дискретное преобразование Фурье, вычисленное без заполнения
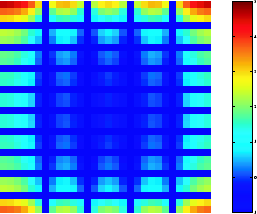
Этот график отличается от преобразования Фурье, отображаемого при визуализации преобразования Фурье. Во-первых, выборка преобразования Фурье намного грубее. Во-вторых, нулевой частотный коэффициент отображается в левом верхнем углу вместо традиционного расположения в центре.
Чтобы получить более тонкую выборку преобразования Фурье, добавьте нулевое заполнение к f при вычислении его DFT. Вычисление заполнения нуля и DFT может быть выполнено за один шаг с помощью этой команды.
F = fft2(f,256,256);
Эта команда содержит нулевые подушки f быть 256 на 256 перед вычислением DFT.
imshow(log(abs(F)),[-1 5]); colormap(jet); colorbar
Дискретное преобразование Фурье, вычисленное с помощью заполнения
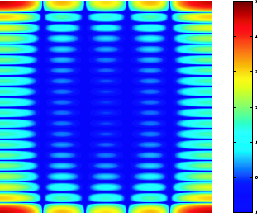
Однако нулевой частотный коэффициент по-прежнему отображается в левом верхнем углу, а не в центре. Эту проблему можно устранить с помощью функции fftshift, который обменивается квадрантами F так, что нулевой частотный коэффициент находится в центре.
F = fft2(f,256,256);F2 = fftshift(F); imshow(log(abs(F2)),[-1 5]); colormap(jet); colorbar
Полученный график идентичен графику, показанному в разделе Визуализация преобразования Фурье.
В этом разделе представлены некоторые из многих приложений преобразования Фурье, связанных с обработкой изображений.
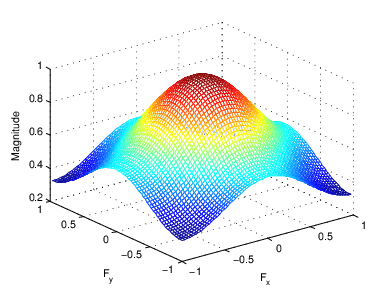
Преобразование Фурье импульсной характеристики линейного фильтра дает частотную характеристику фильтра. Функция freqz2 вычисляет и отображает частотную характеристику фильтра. Частотная характеристика ядра свертки Гаусса показывает, что этот фильтр проходит низкие частоты и ослабляет высокие частоты.
h = fspecial('gaussian');
freqz2(h)Частотная характеристика гауссова фильтра
Дополнительные сведения о линейной фильтрации, проектировании фильтров и частотных характеристиках см. в разделе Проектирование линейных фильтров в частотной области.
В этом примере показано, как выполнить быструю свертку двух матриц с помощью преобразования Фурье. Ключевым свойством преобразования Фурье является то, что умножение двух преобразований Фурье соответствует свертке связанных пространственных функций. Это свойство вместе с быстрым преобразованием Фурье составляет основу для алгоритма быстрой свертки.
Примечание.Метод свертки на основе БПФ чаще всего используется для больших входов. Для небольших вводов, как правило, быстрее использовать imfilter функция.
Создайте две простые матрицы, A и B. A является матрицей M-by-N и B представляет собой матрицу P-by-Q.
A = magic(3); B = ones(3);
Нулевая подушка A и B так, чтобы они были по меньшей мере (M + P-1) -by- (N + Q-1). (ЧастоA и B заполнены нулями до размера, который является степенью 2, потому что fft2 является самым быстрым для этих размеров.) В примере подушечки матрицы должны быть 8 на 8.
A(8,8) = 0; B(8,8) = 0;
Вычисление двухмерного DFT A и B с использованием fft2 функция. Умножьте два DFT вместе и вычислите обратное двумерное DFT результата, используя ifft2 функция.
C = ifft2(fft2(A).*fft2(B));
Извлеките ненулевую часть результата и удалите мнимую часть, вызванную ошибкой округления.
C = C(1:5,1:5); C = real(C)
C = 5×5
8.0000 9.0000 15.0000 7.0000 6.0000
11.0000 17.0000 30.0000 19.0000 13.0000
15.0000 30.0000 45.0000 30.0000 15.0000
7.0000 21.0000 30.0000 23.0000 9.0000
4.0000 13.0000 15.0000 11.0000 2.0000
В этом примере показано, как использовать преобразование Фурье для выполнения корреляции, которая тесно связана со сверткой. Корреляция может использоваться для определения местоположения элементов в изображении. В этом контексте корреляцию часто называют сопоставлением шаблонов.
Считывание образца изображения в рабочую область.
bw = imread('text.png');Создайте шаблон для сопоставления путем извлечения буквы «a» из изображения. Обратите внимание, что шаблон также можно создать с помощью интерактивного синтаксиса imcrop функция.
a = bw(32:45,88:98);
Вычислите корреляцию изображения шаблона с исходным изображением, повернув изображение шаблона на 180 градусов, а затем используя метод свертки на основе БПФ. (Свертка эквивалентна корреляции при повороте ядра свертки на 180 градусов.) Чтобы сопоставить шаблон с изображением, используйте fft2 и ifft2 функции. На получившемся изображении яркие пики соответствуют вхождениям буквы.
C = real(ifft2(fft2(bw) .* fft2(rot90(a,2),256,256)));
figure
imshow(C,[]) % Scale image to appropriate display range.
Чтобы просмотреть расположение шаблона в изображении, найдите максимальное значение пикселя, а затем определите пороговое значение, которое меньше этого максимума. Пороговое изображение показывает расположение этих пиков в виде белых пятен в пороговом корреляционном изображении. (Чтобы облегчить просмотр местоположений на этом рисунке, пример расширяет пороговое изображение, увеличивая размер точек.)
max(C(:))
ans = 68
thresh = 60; % Use a threshold that's a little less than max. D = C > thresh; se = strel('disk',5); E = imdilate(D,se); figure imshow(E) % Display pixels with values over the threshold.
