В LTE имеются два сигнала синхронизации нисходящей линии связи, которые используются UE для получения идентификатора соты и синхронизации кадра.
Первичный сигнал синхронизации (PSS)
Вторичный сигнал синхронизации (SSS)
Деление на два сигнала направлено на уменьшение сложности процесса поиска ячейки.
Физическая идентичность ячейки, , определяется уравнением:
NID (2)
) является группой идентификации ячейки физического уровня (от 0 до 167).
) - идентификатор внутри группы (от 0 до 2 ).
Эта компоновка создает 504 уникальных физических идентификатора соты.
Первичный сигнал синхронизации (PSS) связан с идентификацией соты в группе ()). Вторичный сигнал синхронизации (SSS) связан с группой идентификации соты 1)) и идентификацией соты в группе (2 )).
NID ) можно получить путем успешной демодуляции PSS. Затем SSS может быть демодулирован и объединен со знанием 2) для (1). После установки значений (1) NID (2) можно определить ячейки
Первичный сигнал синхронизации (PSS) основан на последовательности Zadoff-Chu в частотной области.
Последовательности Задоффа-Чу являются конструкцией последовательностей Франка-Задоффа, определенных D. C. Чу в [1]. Эти коды имеют полезное свойство иметь нулевую циклическую автокорреляцию на всех ненулевых лагах. При использовании в качестве кода синхронизации корреляция между идеальной последовательностью и принятой последовательностью является наибольшей, когда отставание равно нулю. Когда существует какое-либо отставание между двумя последовательностями, корреляция равна нулю. Это свойство показано на этом рисунке.
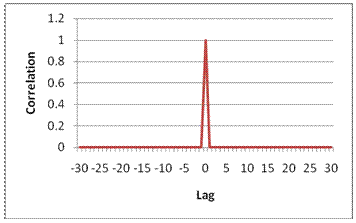
PSS представляет собой последовательность комплексных символов длиной 62 символа.
Последовательность ), используемая для PSS, формируется в соответствии со следующими уравнениями :
= 0,1,..., 30
n = 31,32,..., 61
В предыдущем уравнении u является индексом корневой последовательности Задоффа-Чу и зависит от идентичности ячейки в группе ).
| ) | Корневой индекс u |
|---|---|
| 0 | 25 |
| 1 | 29 |
| 2 | 34 |
PSS отображается в первые 31 поднесущие на каждой стороне поднесущей DC. Следовательно, PSS использует шесть блоков ресурсов с пятью зарезервированными поднесущими на каждой стороне, как показано на этом рисунке.
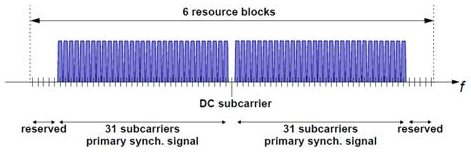
Поскольку поднесущая DC не содержит информации в LTE, это соответствует отображению на средние 62 поднесущие в символе OFDM в сетке ресурсов. d (n) отображается из самой низкой поднесущей в самую высокую поднесущую. PSS отображается на различные символы OFDM в зависимости от того, какой тип кадра используется. Тип кадра 1 - дуплексный режим с частотным разделением каналов (FDD), тип кадра 2 - дуплексный режим с временным разделением каналов (TDD ).
FDD - PSS отображается на последний символ OFDM в слотах 0 и 10, как показано на этом рисунке.
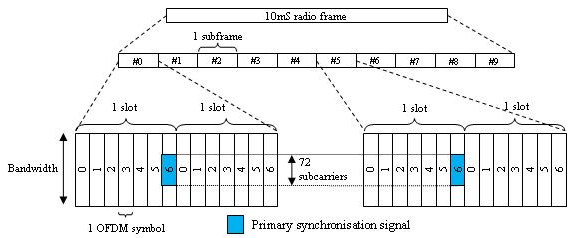
TDD - PSS отображается на третий символ OFDM в подкадрах 1 и 6, как показано на этом рисунке.
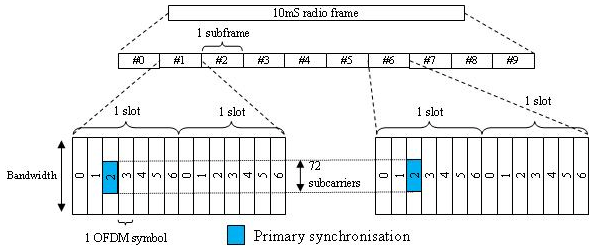
Вторичный сигнал синхронизации (SSS) основан на последовательностях максимальной длины (m-последовательностях).
M-последовательность представляет собой псевдослучайную двоичную последовательность, которая может быть создана циклически в каждом возможном состоянии сдвигового регистра длины m, что приводит к последовательности длины 2m-1. Три m-последовательности, каждая длиной 31, используются для генерации сигналов синхронизации, обозначенных , и .
Две двоичные последовательности, каждая длиной 31, используются для генерации SSS. Последовательности s0 (m0) и s1 (m1) представляют собой различные циклические сдвиги m-последовательностиs˜. Индексы m0 и m1 получают из группы идентичности ячейки NID (2) и определяют циклический сдвиг. Значения можно прочитать из таблицы 6.11.2.1-1 в [2].
Две последовательности скремблируются двоичным скремблирующим кодом (c0 (n), c1 (n)), который зависит от NID (2).
Вторая последовательность SSS, используемая в каждом кадре радиосвязи, скремблируется двоичным скремблирующим кодом (z1 (m0), z1 (m1)), соответствующим значению циклического сдвига первой последовательности, передаваемой в кадре радиосвязи.
Последовательности s0 (m0) и s1 (m1) задаются следующими уравнениями:
mod 31)
mod 31)
генерируется из примитивного многочлена + 1 над конечным полем GF (2).
c0 (n) и c1 (n даны следующими уравнениями:
mod 31)
) mod 31)
генерируется из примитивного многочлена + 1 над конечным полем GF (2).
z1 (m0) и z1 (m1) задаются следующими уравнениями:
mod 31)
mod 31)
генерируется из примитивного многочлена + x + 1 над конечным полем GF (2).
Скремблированные последовательности перемежаются, чтобы чередовать последовательность, передаваемую в первой и второй SSS-передаче в каждом кадре радиосвязи. Это позволяет приемнику определять синхронизацию кадра из наблюдения только одной из двух последовательностей; если первый наблюдаемый сигнал SSS находится в субкадре 0 или субкадре 5, синхронизация может быть достигнута, когда сигнал SSS наблюдается в субкадре 0 или субкадре 5 следующего кадра.
Как и в случае PSS, SSS отображается на различные символы OFDM в зависимости от того, какой тип кадра используется:
FDD - SSS передается в том же подкадре, что и PSS, но одним символом OFDM ранее. SSS отображается на те же поднесущие (средние 72 поднесущих), что и PSS.
TDD - SSS отображается на последний символ OFDM в слотах 1 и 11, который представляет собой три символа OFDM перед PSS.
SSS строится с использованием различных скремблирующих последовательностей при отображении на четные и нечетные элементы ресурса.
Даже элементы ресурсов:
Субкадр 0: c0 (n)
Подкадр 5: c0 (n)
Нечетные элементы ресурсов:
Подкадр 0: z1 (m0) (n)
Подкадр 5: z1 (m1) (n)
d (n) отображается из самой низкой поднесущей в самую высокую поднесущую .
[1] Чу, Д.С. «Многофазные коды с хорошими свойствами периодической корреляции». IEEE Trans. Inf. Теория. Том 18, номер 4, июль 1972, стр. 531-532.
[2] 3GPP TS 36.211. "Развитый универсальный наземный радиодоступа (E-UTRA); Физические каналы и модуляция. "Проект партнерства 3-го поколения; Техническая спецификация на сеть радиодоступа группы. URL: https://www.3gpp.org.
lteCellSearch | lteDLFrameOffset | lteDLResourceGrid | ltePSS | ltePSSIndices | lteSSS | lteSSSIndices | zadoffChuSeq