Мэпмейкеры разработали сотни картографических проекций, за несколько тысяч лет. Общепризнано три больших семейства проекций карт, а также несколько более мелких. Они основаны на типах геометрических форм, которые используются для переноса элементов из сферы или сфероида в плоскость. Проекции карт основаны на проявляемых поверхностях, и три традиционных семейства состоят из цилиндров, конусов и плоскостей. Они используются для классификации большинства проекций, включая некоторые, которые не построены аналитически (геометрически). Кроме того, ряд картографических проекций основан на многогранниках. Хотя многогранные проекции обладают интересными и полезными свойствами, они не описаны в данном руководстве.
Какая развиваемая поверхность будет использоваться для проекции, зависит от того, какая область должна быть отображена, ее географическая протяженность и геометрические свойства, которые должны иметь области, границы и трассы, учитывая назначение карты. В следующих разделах описано и проиллюстрировано, как создаются цилиндрические, конические и азимутальные семейства проекций карты, и приведены некоторые примеры проекций, которые основаны на них.
Цилиндрический выступ получают путем обертывания цилиндра вокруг земного шара, представляющего Землю. Проекция карты представляет собой изображение земного шара, спроецированного на цилиндрическую поверхность, которая затем разворачивается в плоскую поверхность. При выравнивании цилиндра по полярной оси параллели отображаются в виде горизонтальных линий, а меридианы - в виде вертикальных линий. Цилиндрические выступы могут быть равными по площади, конформными или равноудаленными. На следующем рисунке показана правильная цилиндрическая или нормальная пространственная ориентация, при которой цилиндр является касательным к Земле вдоль экватора, а проекция излучается горизонтально от оси вращения. Метод проекции показан слева, а справа приведен пример (цилиндрическая проекция равной площади, нормальный/экваториальный аспект).
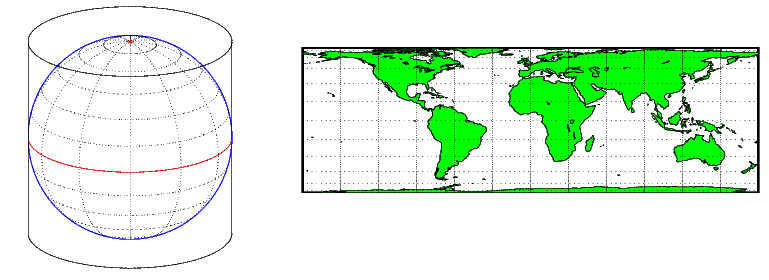
Описание проекционного аспекта см. в разделе Проекционный аспект.
Некоторые широко используемые цилиндрические проекции карты
Цилиндрический выступ равной площади
Равноудаленная цилиндрическая проекция
Проекция Меркатора
Проекция Мельника
Плита Карре проекция
Универсальная поперечная проекция Меркатора
Все цилиндрические выступы заполняют прямоугольную плоскость. Псевдоцилиндрические проекционные контуры имеют тенденцию быть скорее бочкообразными, чем прямоугольными. Однако они действительно напоминают цилиндрические проекции, с прямыми и параллельными линиями широты, и могут иметь равноотстоящие меридианы, но меридианы являются кривыми, а не прямыми. Псевдоцилиндрические выступы могут быть равной площади, но не являются конформными или равноудаленными.
Некоторые широко используемые псевдоцилиндрические картографические проекции
Проекции Экерта (I-VI)
Гомолозиновая проекция Гуда
Проекция Моллвайда
Квартальная авторская проекция
Проекция Робинсона
Синусоидальная проекция
Коническая проекция выводится из проекции земного шара на размещенный над ним конус. Для нормального аспекта вершина конуса лежит на полярной оси Земли. Если конус касается Земли только на одной конкретной параллели широты, он называется касательным. Если сделать меньше, конус будет пересекать Землю дважды, в этом случае он называется секущим. Конические выступы часто достигают меньшего искажения в средних и высоких широтах, чем цилиндрические выступы. Дальнейшим уточнением является поликоническая проекция, которая разворачивает семейство касательных или секущих конусов для скрепления в скобки последовательности полос параллелей для получения еще меньшего искажения масштаба. На следующем рисунке показана коническая проекция, изображающая ее конструкцию слева, с примером справа (проекция равной площади Альберса, полярный аспект).
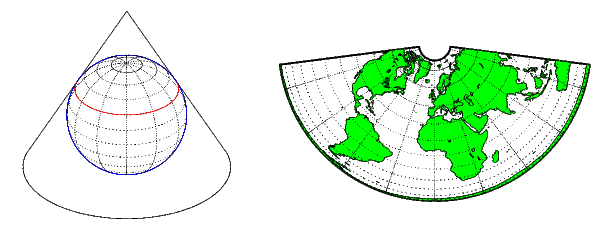
Некоторые широко используемые конические проекции
Проекция равной площади
Эквидистантная проекция
Конформная проекция Ламберта
Поликоническая проекция
Азимутальная проекция - проекция земного шара на плоскость. В полярном аспекте азимутальная проекция отображает плоскость, касательную к Земле на одном из полюсов, с меридианами, проецируемыми как прямые, излучающие из полюса, и параллелями, показанными как полные окружности, центрированные на полюсе. Азимутальные проекции (особенно ортографические) могут иметь экваториальные или наклонные аспекты. Проекция центрирована на точке, то есть на поверхности, в центре Земли, у антипода, на некотором расстоянии за Землей, или на бесконечности. Большинство азимутальных проекций не подходят для отображения всей Земли в одном виде, но дают ощущение земного шара. Следующий рисунок иллюстрирует азимутальную проекцию, изображая её слева, с примером справа (ортогональная проекция, полярный аспект).
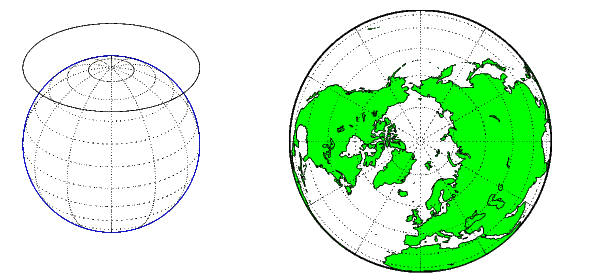
Некоторые широко используемые азимутальные проекции
Эквидистантная азимутальная проекция
Гномоническая проекция
Азимутальная проекция равной площади Ламберта
Ортогональная проекция
Стереографическая проекция
Универсальная полярная стереографическая проекция