Объект преобразования Matrix свойство применяет преобразование ко всем нижестоящим элементам объекта в унисон. Преобразования включают поворот, перемещение и масштабирование. Определите преобразование с помощью матрицы преобразования «четыре на четыре».
makehgtform функция упрощает построение матриц для выполнения вращения, перемещения и масштабирования. Сведения о создании матриц преобразования с помощью makehgtform, см. раздел Преобразования гнезд для сложных движений.
Преобразования поворота следуют правому правилу - вращают объекты вокруг оси X, Y или Z с положительными углами, вращающимися против часовой стрелки, при этом визирование вдоль соответствующей оси в направлении начала координат. Если угол поворота тета, следующая матрица определяет поворот тета вокруг оси X.
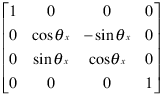
Чтобы создать матрицу преобразования для поворота вокруг произвольной оси, используйте makehgtform функция.
Преобразование перемещаемых объектов относительно их текущего местоположения. Задайте преобразование как расстояния tx, ty и tz в единицах пространства данных. Следующая матрица показывает расположение этих элементов в матрице преобразования.

Преобразования масштабирования изменяют размеры объектов. Задайте масштабные коэффициенты sx, sy и sz и создайте следующую матрицу.
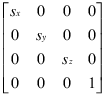
Нельзя использовать масштабные коэффициенты, меньшие или равные нулю.
Преобразование по умолчанию - это единичная матрица, которую можно создать с помощью eye функция. Вот единичная матрица.

См. раздел Отмена операций преобразования.
Преобразования перспективы изменяют расстояние, на котором просматривается объект. Следующая матрица является примером матрицы перспективного преобразования, что не допускается графикой MATLAB ®.
В этом случае px является фактором перспективы.
Сдвигающие преобразования сохраняют все точки вдоль заданной линии (или плоскости, в 3-D координатах) фиксированными при смещении всех других точек параллельно прямой (плоскости), пропорциональных их перпендикулярному расстоянию от фиксированной линии (плоскости). Следующая матрица является примером матрицы сдвигового преобразования, которая hgtransform не позволяет.
В этом случае sx является коэффициентом сдвига и может заменить любой нулевой элемент в единичной матрице.
Преобразования задаются в абсолютных величинах, а не относительно текущего преобразования. Например, если применить преобразование, которое перемещает объект преобразования на 5 единиц в направлении x, а затем применить другое преобразование, которое перемещает его на 4 единицы в направлении y, результирующее положение объекта будет равняться 4 единицам в направлении y от его исходного положения.
Для накопления преобразований необходимо объединить отдельные преобразования в одну матрицу. См. раздел Объединение преобразований в одну матрицу.
Обычно эффективнее объединить различные операции преобразования в одну матрицу путем объединения (умножения) отдельных матриц и установки Matrix свойство к результату. Матричное умножение не коммутативно, поэтому порядок умножения матриц влияет на результат.
Например, предположим, что требуется выполнить операцию масштабирования, преобразования и последующего поворота. Принятие R, T и S являются индивидуальными матрицами преобразования, умножайте матрицы следующим образом:
C = R*T*S % operations are performed from right to left
S - матрица масштабирования, T - матрица преобразования, R является матрицей вращения, и C является составным элементом трех операций. Затем задайте объект преобразования Matrix свойство для C:
hg = hgtransform('Matrix',C);
Следующие наборы операторов не эквивалентны. Первый набор:
hg.Matrix = C; hg.Matrix = eye(4);
приводит к удалению преобразования C. Второй набор:
I = eye(4); C = I*R*T*S; hg.Matrix = C;
применяет преобразование C. Конкатенация единичной матрицы с другими матрицами не влияет на композитную матрицу.
Поскольку операции преобразования задаются в абсолютном выражении (не относительно текущего преобразования), можно отменить ряд преобразований, установив текущее преобразование в единичную матрицу. Например:
hg = hgtransform('Matrix',C); ... hg.Matrix = eye(4);
возвращает объекты, содержащиеся в объекте преобразования, hg, к их ориентации перед применением преобразования C.
Дополнительные сведения о матрице идентификаторов см. в разделе eye функция
eye | hgtransform | makehgtform