Реализация связанных списков с классами

Код определения класса

Описание кода определения класса см. в разделе Описание класса dlnode.

Чтобы использовать класс, создайте папку с именем @dlnode и сохранить dlnode.m в эту папку. Родительская папка @dlnode должен находиться в тракте MATLAB ®. Также можно сохранитьdlnode.m к папке пути.

`dlnode` Дизайн класса

dlnode является классом для создания двойных связанных списков, в которых каждый узел содержит:

Массив данных
Переход к следующему узлу
Дескриптор к предыдущему узлу

Каждый узел имеет методы, которые позволяют узлу быть:

Вставляется перед указанным узлом в списке связей
Вставляется после определенного узла в связанный список
Удалено из списка

Свойства класса

dlnode класс реализует каждый узел как объект-дескриптор с тремя свойствами:

Data - Содержит данные для этого узла
Next - Содержит дескриптор следующего узла в списке (SetAccess = private)
Prev - Содержит дескриптор предыдущего узла в списке (SetAccess = private)

На этой схеме показан список с тремя узлами n1, n2, и n3. Здесь также показано, как узлы ссылаются на следующий и предыдущий узлы.

Методы классов

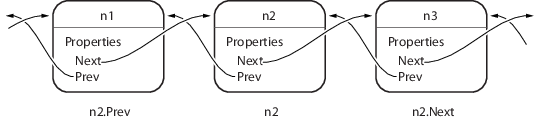
dlnode класс реализует следующие методы:

dlnode - Построить узел и назначить значение, переданное в качестве входных данных Data собственность
insertAfter - Вставить этот узел после указанного узла
insertBefore - Вставить этот узел перед указанным узлом
removeNode - Удаление этого узла из списка и повторное подключение оставшихся узлов
clearList - Эффективное удаление больших списков
delete - частный метод, вызываемый MATLAB при удалении списка.

Создать список двойных связей

Создание узла путем передачи данных узла в dlnode конструктор класса. Например, эти инструкции создают три узла со значениями данных 1, 2, и 3:

n1 = dlnode(1);
n2 = dlnode(2);
n3 = dlnode(3);

Создайте эти узлы в список с двойными связями, используя методы классов, разработанные для этой цели:

n2.insertAfter(n1) % Insert n2 after n1
n3.insertAfter(n2) % Insert n3 after n2

Теперь три узла связаны:

n1.Next % Points to n2

ans = 

  dlnode with properties:

    Data: 2
    Next: [1x1 dlnode]
    Prev: [1x1 dlnode]

n2.Next.Prev % Points back to n2

ans = 

  dlnode with properties:

    Data: 2
    Next: [1x1 dlnode]
    Prev: [1x1 dlnode]

n1.Next.Next % Points to n3

ans = 

  dlnode with properties:

    Data: 3
    Next: []
    Prev: [1x1 dlnode]

n3.Prev.Prev % Points to n1

ans = 

  dlnode with properties:

    Data: 1
    Next: [1x1 dlnode]
    Prev: []

Почему класс дескриптора для связанных списков?

Каждый узел уникален тем, что два узла не могут предшествовать одному узлу или располагаться рядом с ним.

Например, объект узла, node, содержит в себе Next свойство дескриптор объекта следующего узла, node.Next. Аналогично, Prev содержит дескриптор предыдущего узла, node.Prev. Используя список трехузловых связей, определенный в предыдущем разделе, можно продемонстрировать, что следующие операторы верны:

n1.Next == n2
n2.Prev == n1

Теперь предположим, что вы назначили n2 кому x:

x = n2;

Следующие два равенства верны:

x == n1.Next
x.Prev == n1

Но каждый экземпляр узла уникален, поэтому в списке есть только один узел, который может удовлетворять условиям равенства n1.Next и имеющие Prev свойство, содержащее дескриптор для n1. Поэтому x должен указывать на тот же узел, что и n2.

Должен существовать способ ссылки нескольких переменных на один и тот же объект. MATLAB handle класс обеспечивает средство для обоих x и n2 для ссылки на один и тот же узел.

Класс дескриптора определяет eq метод (использование methods('handle') для перечисления методов класса дескрипторов), что позволяет использовать == оператор со всеми объектами-дескрипторами.

Связанная информация

Дополнительные сведения о классах дескрипторов см. в разделе Сравнение классов дескрипторов и значений.

`dlnode` Синопсис класса

В этом разделе описывается реализация dlnode класс.

Пример кода	Обсуждение
classdef dlnode < handle	Конструкция класса dlnode Почему класс дескриптора для связанных списков? Сравнение классов дескрипторов и значений
properties Data end	Конструкция класса dlnode
properties (SetAccess = private) Next = dlnode.empty Prev = dlnode.empty end	Атрибуты свойства: `SetAccess`. Инициализировать эти свойства для `empty` `dlnode` объекты. Общие сведения о свойствах см. в разделе Синтаксис свойств
methods	Общие сведения о методах см. в разделе Методы проектирования классов
function node = dlnode(Data) if (nargin > 0) node.Data = Data; end end	Для создания отдельного узла (не подключенного) требуются только данные. Общие сведения о конструкторах см. в разделе Рекомендации по конструкторам.
function insertAfter(newNode, nodeBefore) removeNode(newNode); newNode.Next = nodeBefore.Next; newNode.Prev = nodeBefore; if ~isempty(nodeBefore.Next) nodeBefore.Next.Prev = newNode; end nodeBefore.Next = newNode; end	Вставка узла в список двойных связей после указанного узла или связывание двух указанных узлов, если список еще не существует. Назначает правильные значения для `Next` и `Prev` свойства. Вставить узлы
function insertBefore(newNode, nodeAfter) removeNode(newNode); newNode.Next = nodeAfter; newNode.Prev = nodeAfter.Prev; if ~isempty(nodeAfter.Prev) nodeAfter.Prev.Next = newNode; end nodeAfter.Prev = newNode; end	Вставка узла в список двойных связей перед указанным узлом или связывание двух указанных узлов, если список еще не существует. Этот метод присваивает правильные значения `Next` и `Prev` свойства. См. Вставка узлов
function removeNode(node) if ~isscalar(node) error('Nodes must be scalar') end prevNode = node.Prev; nextNode = node.Next; if ~isempty(prevNode) prevNode.Next = nextNode; end if ~isempty(nextNode) nextNode.Prev = prevNode; end node.Next = = dlnode.empty; node.Prev = = dlnode.empty; end	Удалите узел и исправьте список, чтобы остальные узлы были правильно подключены. `node` аргумент должен быть скалярным. Если ссылки на узел отсутствуют, MATLAB удаляет его. Удаление узла
function clearList(node) prev = node.Prev; next = node.Next; removeNode(node) while ~isempty(next) node = next; next = node.Next; removeNode(node); end while ~isempty(prev) node = prev; prev = node.Prev; removeNode(node) end end	Избегайте рекурсивных вызовов деструктора в результате очистки переменной списка. Закольцовывание списка для разъединения каждого узла. При отсутствии ссылок на узел MATLAB вызывает деструктор класса (см. `delete` метод) перед удалением.
methods (Access = private) function delete(node) clearList(node) end	Метод деструктора класса. MATLAB вызывает `delete` удаление узла, который все еще подключен к списку.
end end	Конец частных методов и конец определения класса.

Развернуть для кода класса

classdef dlnode < handle
   % dlnode A class to represent a doubly-linked node.
   % Link multiple dlnode objects together to create linked lists.
   properties
      Data
   end
   properties(SetAccess = private)
      Next = dlnode.empty
      Prev = dlnode.empty
   end
   
   methods
      function node = dlnode(Data)
         % Construct a dlnode object
         if nargin > 0
            node.Data = Data;
         end
      end
      
      function insertAfter(newNode, nodeBefore)
         % Insert newNode after nodeBefore.
         removeNode(newNode);
         newNode.Next = nodeBefore.Next;
         newNode.Prev = nodeBefore;
         if ~isempty(nodeBefore.Next)
            nodeBefore.Next.Prev = newNode;
         end
         nodeBefore.Next = newNode;
      end
      
      function insertBefore(newNode, nodeAfter)
         % Insert newNode before nodeAfter.
         removeNode(newNode);
         newNode.Next = nodeAfter;
         newNode.Prev = nodeAfter.Prev;
         if ~isempty(nodeAfter.Prev)
            nodeAfter.Prev.Next = newNode;
         end
         nodeAfter.Prev = newNode;
      end
      
      function removeNode(node)
         % Remove a node from a linked list.
         if ~isscalar(node)
            error('Input must be scalar')
         end
         prevNode = node.Prev;
         nextNode = node.Next;
         if ~isempty(prevNode)
            prevNode.Next = nextNode;
         end
         if ~isempty(nextNode)
            nextNode.Prev = prevNode;
         end
         node.Next = dlnode.empty;
         node.Prev = dlnode.empty;
      end
      
      function clearList(node)
         % Clear the list before
         % clearing list variable
         prev = node.Prev;
         next = node.Next;
         removeNode(node)
         while ~isempty(next)
            node = next;
            next = node.Next;
            removeNode(node);
         end
         while ~isempty(prev)
            node = prev;
            prev = node.Prev;
            removeNode(node)
         end
      end
   end
   
   methods (Access = private)
      function delete(node)
         clearList(node)
      end
   end
end

Свойства класса

Только dlnode методы класса могут устанавливать Next и Prev свойства, поскольку эти свойства имеют доступ к частному набору (SetAccess = private). Использование доступа к частному аппарату предотвращает выполнение кодом клиента неправильной операции с этими свойствами. dlnode методы класса выполняют все операции, разрешенные на этих узлах.

Data свойство имеет открытый набор и доступ, позволяющий запрашивать и изменять значение Data при необходимости.

Вот как dlnode класс определяет свойства:

properties
   Data
end
properties(SetAccess = private)
   Next = dlnode.empty;
   Prev = dlnode.empty;
end

Создание объекта узла

Чтобы создать объект узла, укажите данные узла в качестве аргумента конструктора:

function node = dlnode(Data)
   if nargin > 0
      node.Data = Data;
   end
end

Вставить узлы

Существует два метода вставки узлов в список - insertAfter и insertBefore. Эти методы выполняют аналогичные операции, поэтому в этом разделе описываются только insertAfter подробно.

function insertAfter(newNode, nodeBefore)
   removeNode(newNode);
   newNode.Next = nodeBefore.Next;
   newNode.Prev = nodeBefore;
   if ~isempty(nodeBefore.Next)
      nodeBefore.Next.Prev = newNode;
   end
   nodeBefore.Next = newNode;
end

Как insertAfter Работает. Во-первых, insertAfter вызывает removeNode чтобы гарантировать, что новый узел не подключен к другим узлам. Затем, insertAfter назначает newNode Next и Prev свойства для дескрипторов узлов, которые находятся после и перед newNode расположение в списке.

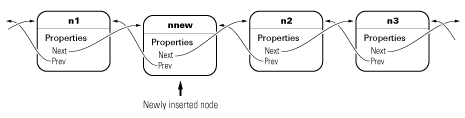
Например, предположим, что требуется вставить новый узел, nnew, после существующего узла, n1, в списке, содержащем n1—n2—n3.

Сначала создайте nnew:

nnew = dlnode(rand(3));

Далее, звонок insertAfter вставить nnew в список после n1:

nnew.insertAfter(n1)

insertAfter метод выполняет следующие шаги для вставки nnew в списке между n1 и n2:

Набор nnew.Next кому n1.Next (n1.Next является n2):
```
nnew.Next = n1.Next;
```
Набор nnew.Prev кому n1
```
nnew.Prev = n1;
```
Если n1.Next не пуст, то n1.Next по-прежнему n2, так n1.Next.Prev является n2.Prev, для которого установлено значение nnew
```
n1.Next.Prev = nnew;
```
n1.Next теперь имеет значение nnew
```
n1.Next = nnew;
```

Удаление узла

removeNode метод удаляет узел из списка и повторно подключает оставшиеся узлы. insertBefore и insertAfter методы всегда вызывают removeNode на узле, который требуется вставить, прежде чем пытаться подключить его к связанному списку.

Запрос removeNode гарантирует, что узел находится в известном состоянии, прежде чем назначить его Next или Prev свойство:

function removeNode(node)
   if ~isscalar(node)
      error('Input must be scalar')
   end
   prevNode = node.Prev;
   nextNode = node.Next;
   if ~isempty(prevNode)
      prevNode.Next = nextNode;
   end
   if ~isempty(nextNode)
      nextNode.Prev = prevNode;
   end
   node.Next = dlnode.empty;
   node.Prev = dlnode.empty;
end

Например, предположим, что вы удалили n2 из трехузлового списка (n1–n2–n3):

n2.removeNode;

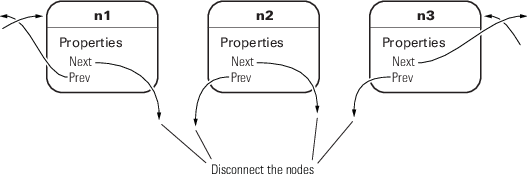
removeNode удаляет n2 из списка и повторно подключает оставшиеся узлы с помощью следующих шагов:

n1 = n2.Prev;
n3 = n2.Next;
if n1 exists, then
   n1.Next = n3;
if n3 exists, then
   n3.Prev = n1

Список вновь присоединен, поскольку n1 подключается к n3 и n3 подключается к n1. Последним шагом является обеспечение того, чтобы n2.Next и n2.Prev оба пусты (то есть n2 не подключен):

n2.Next = dlnode.empty;
n2.Prev = dlnode.empty;

Удаление узла из списка

Предположим, что создается список с 10 узлами и сохраняется маркер перемещения в заголовке списка:

head = dlnode(1);
for i = 10:-1:2
   new = dlnode(i);
   insertAfter(new,head);
end

Теперь удалите третий узел (Data свойству присвоено значение 3):

removeNode(head.Next.Next)

Теперь третий узел в списке имеет значение данных 4:

head.Next.Next

ans = 

  dlnode with properties:

    Data: 4
    Next: [1x1 dlnode]
    Prev: [1x1 dlnode]

И предыдущий узел имеет Data значение 2:

head.Next

ans = 

  dlnode with properties:

    Data: 2
    Next: [1x1 dlnode]
    Prev: [1x1 dlnode]

Удаление узла

Чтобы удалить узел, вызовите removeNode метод на этом узле. removeNode метод разъединяет узел и повторно подключает список, прежде чем разрешить MATLAB уничтожить удаленный узел. MATLAB уничтожает узел после удаления ссылок на него другими узлами и повторного подключения списка.

Удалить список

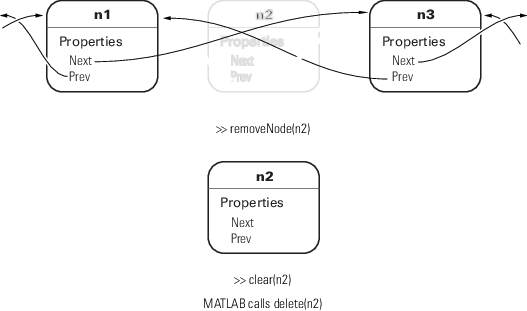
При создании связанного списка и назначении переменной, содержащей, например, заголовок или конец списка, удаление этой переменной приводит к рекурсии деструктора по всему списку. При наличии достаточно большого списка очистка переменной списка может привести к превышению предела рекурсии MATLAB.

clearList метод позволяет избежать рекурсии и повысить производительность удаления больших списков путем закольцовывания списка и отключения каждого узла. clearList принимает дескриптор любого узла в списке и удаляет оставшиеся узлы.

function clearList(node)
   if ~isscalar(node)
      error('Input must be scalar')
   end
   prev = node.Prev;
   next = node.Next;
   removeNode(node)
   while ~isempty(next)
      node = next;
      next = node.Next;
      removeNode(node);
   end
   while ~isempty(prev)
      node = prev;
      prev = node.Prev;
      removeNode(node)
   end
end

Например, предположим, что создается список со многими узлами:

head = dlnode(1);
for k = 100000:-1:2
   nextNode = dlnode(k);
   insertAfter(nextNode,head)
end

Переменная head содержит дескриптор узла в начале списка:

head

head = 

  dlnode with properties:

    Data: 1
    Next: [1x1 dlnode]
    Prev: []

head.Next

ans = 

  dlnode with properties:

    Data: 2
    Next: [1x1 dlnode]
    Prev: [1x1 dlnode]

Вы можете позвонить clearList для удаления всего списка:

clearList(head)

Единственными узлами, которые не были удалены MATLAB, являются узлы, для которых существует явная ссылка. В этом случае эти ссылки head и nextNode:

head

head = 

  dlnode with properties:

    Data: 1
    Next: []
    Prev: []

nextNode

nextNode = 

  dlnode with properties:

    Data: 2
    Next: []
    Prev: []

Можно удалить эти узлы, очистив переменные:

clear head nextNode

Метод удаления

delete метод просто вызывает clearList способ:

methods (Access = private)
   function delete(node)
      clearList(node)
   end
end

delete метод имеет частный доступ для предотвращения вызовов пользователей delete при намерении удалить один узел. Вызовы MATLAB delete неявно при уничтожении списка.

Чтобы удалить один узел из списка, используйте removeNode способ.

Специализироваться на `dlnode` Класс

dlnode класс реализует двойной связанный список и обеспечивает удобную отправную точку для создания более специализированных типов связанных списков. Например, предположим, что требуется создать список, в котором каждый узел будет иметь имя.

Вместо копирования кода, используемого для реализации dlnode класс, а затем разворачивая его, можно вывести новый класс из dlnode (то есть подкласс dlnode). Можно создать класс, который имеет все возможности dlnode а также определяет свои собственные дополнительные особенности. И потому что dlnode является классом дескриптора, этот новый класс также является классом дескриптора.

`NamedNode` Определение класса

Чтобы использовать класс, создайте папку с именем @NamedNode и сохранить NamedNode.m в эту папку. Родительская папка @NamedNode должен находиться в пути MATLAB. Также можно сохранить NamedNode.m к папке пути.

Следующее определение класса показывает, как получить NamedNode класс из dlnode класс:

classdef NamedNode < dlnode
   properties
      Name = ''
   end
   methods
      function n = NamedNode (name,data)
         if nargin == 0
            name = '';
            data = [];
         end
         n = n@dlnode(data);
         n.Name = name;
      end
   end
end

NamedNode класс добавляет Name для хранения имени узла.

Конструктор вызывает конструктор класса для dlnode класс, а затем присваивает значение Name собственность.

Использовать `NamedNode` Создание списка двойных связей

Используйте NamedNode класс, как dlnode класс, за исключением указания имени для каждого объекта узла. Например:

n(1) = NamedNode('First Node',100);
n(2) = NamedNode('Second Node',200);
n(3) = NamedNode('Third Node',300);

Теперь используйте методы вставки, унаследованные от dlnode для построения списка:

n(2).insertAfter(n(1))
n(3).insertAfter(n(2))

Один узел отображает свое имя и данные при запросе его свойств:

n(1).Next

ans = 

  NamedNode with properties:

    Name: 'Second Node'
    Data: 200
    Next: [1x1 NamedNode]
    Prev: [1x1 NamedNode]

n(1).Next.Next

ans = 

  NamedNode with properties:

    Name: 'Third Node'
    Data: 300
    Next: []
    Prev: [1x1 NamedNode]

n(3).Prev.Prev

ans = 

  NamedNode with properties:

    Name: 'First Node'
    Data: 100
    Next: [1x1 NamedNode]
    Prev: []

Связанные темы

Суперкласс дескриптора

Документация