Обнаружение и замена отклонений в данных
B = filloutliers(A,fillmethod)A и заменяет их в соответствии с fillmethod. Например, filloutliers(A,'previous') заменяет отклонения предыдущим элементом, не являющимся отклонениями. По умолчанию отклонение является значением, которое больше трех масштабированных абсолютных отклонений медианы (MAD) от медианы. Если A является матрицей или таблицей, то filloutliers работает по каждому столбцу отдельно. Если A является многомерным массивом, то filloutliers работает вдоль первого размера, размер которого не равен 1.
B = filloutliers(A,fillmethod,findmethod)filloutliers(A,'previous','mean') определяет отклонение как элемент A более трех стандартных отклонений от среднего значения.
B = filloutliers(A,fillmethod,'percentiles',threshold)threshold. threshold аргумент - это двухэлементный вектор строки, содержащий нижний и верхний процентильные пороги, такие как [10 90].
B = filloutliers(A,fillmethod,movmethod,window)window. Например, filloutliers(A,'previous','movmean',5) идентифицирует отклонения как элементы с более чем тремя локальными стандартными отклонениями от локального среднего значения в пределах пятиэлементного окна.
B = filloutliers(___,Name,Value)filloutliers(A,'previous','SamplePoints',t) обнаруживает отклонения в A относительно соответствующих элементов вектора времени t.
[ также возвращает информацию о положении отклонений и порогов, вычисленных методом обнаружения. B,TF,L,U,C] = filloutliers(___)TF является логическим массивом, указывающим расположение отклонений в A. L, U, и C аргументы представляют нижний и верхний пороги и значение центра, используемое методом обнаружения отклонений.
Создайте вектор данных, содержащий отклонение, и используйте линейную интерполяцию для замены отклонения. Постройте график исходных и заполненных данных.
A = [57 59 60 100 59 58 57 58 300 61 62 60 62 58 57]; B = filloutliers(A,'linear'); plot(1:15,A,1:15,B,'o') legend('Original Data','Interpolated Data')

Создайте вектор, содержащий отклонение, и определите отклонения как точки за пределами трех стандартных отклонений от среднего значения. Замените отклонение ближайшим элементом, который не является отклонением, и постройте график исходных данных и интерполированных данных.
A = [57 59 60 100 59 58 57 58 300 61 62 60 62 58 57]; B = filloutliers(A,'nearest','mean'); plot(1:15,A,1:15,B,'o') legend('Original Data','Interpolated Data')

Используйте скользящую медиану, чтобы найти локальные отклонения в синусоиде, которая соответствует вектору времени.
Создайте вектор данных, содержащий локальное отклонение.
x = -2*pi:0.1:2*pi; A = sin(x); A(47) = 0;
Создание вектора времени, соответствующего данным в A.
t = datetime(2017,1,1,0,0,0) + hours(0:length(x)-1);
Определите отклонения как точки с более чем тремя локальными масштабами MAD, удаленными от локальной медианы в пределах скользящего окна. Найдите местоположение отклонения в A относительно точек в t с размером окна 5 часов. Заполните отклонение вычисленным пороговым значением с помощью метода 'clip'и постройте график исходных и заполненных данных.
[B,TF,U,L,C] = filloutliers(A,'clip','movmedian',hours(5),'SamplePoints',t); plot(t,A,t,B,'o') legend('Original Data','Filled Data')

Отображение порогового значения, которое заменило отклонение.
L(TF)
ans = -0.8779
Заполните отклонения для каждой строки матрицы.
Создайте матрицу данных, содержащую отклонения по диагонали.
A = randn(5,5) + diag(1000*ones(1,5))
A = 5×5
103 ×
1.0005 -0.0013 -0.0013 -0.0002 0.0007
0.0018 0.9996 0.0030 -0.0001 -0.0012
-0.0023 0.0003 1.0007 0.0015 0.0007
0.0009 0.0036 -0.0001 1.0014 0.0016
0.0003 0.0028 0.0007 0.0014 1.0005
Заполните отклонения нулями на основе данных в каждой строке и просмотрите новые значения.
[B,TF,lower,upper,center] = filloutliers(A,0,2); B
B = 5×5
0 -1.3077 -1.3499 -0.2050 0.6715
1.8339 0 3.0349 -0.1241 -1.2075
-2.2588 0.3426 0 1.4897 0.7172
0.8622 3.5784 -0.0631 0 1.6302
0.3188 2.7694 0.7147 1.4172 0
Можно получить прямой доступ к обнаруженным значениям отклонений и их заполненным значениям с помощью TF в качестве вектора индекса.
[A(TF) B(TF)]
ans = 5×2
103 ×
1.0005 0
0.9996 0
1.0007 0
1.0014 0
1.0005 0
Найдите отклонение в векторе данных и замените его с помощью 'clip' способ. Постройте график исходных данных, заполненных данных и пороговых значений и значения центра, определенных методом обнаружения. 'clip' заменяет отклонение верхним пороговым значением.
x = 1:10; A = [60 59 49 49 58 100 61 57 48 58]; [B,TF,lower,upper,center] = filloutliers(A,'clip'); plot(x,A,x,B,'o',x,lower*ones(1,10),x,upper*ones(1,10),x,center*ones(1,10)) legend('Original Data','Filled Data','Lower Threshold','Upper Threshold','Center Value')

A - Входные данныеВходные данные, указанные как вектор, матрица, многомерный массив, таблица или расписание.
Если A является таблицей, то ее переменные должны быть типа double или singleили вы можете использовать 'DataVariables' пара имя-значение для списка double или single переменные явным образом. Указание переменных полезно при работе с таблицей, содержащей переменные с типами данных, отличными от double или single.
Если A является расписанием, то filloutliers работает только с элементами таблицы. Время строк должно быть уникальным и перечисляться в порядке возрастания.
Типы данных: double | single | table | timetable
fillmethod - Метод заполнения'center' | 'clip' | 'previous' | 'next' | 'nearest' | 'linear' | 'spline' | 'pchip' | 'makima'Метод заполнения для замены отклонений, заданный как числовой скаляр или один из следующих:
| Метод заполнения | Описание |
|---|---|
| Числовой скаляр | Заполняет заданным скалярным значением |
'center' | Заполняет значением центра, определяемым findmethod |
'clip' | Заполняет нижним пороговым значением для элементов меньше нижнего порогового значения, определяемого findmethod. Заполняет верхним пороговым значением для элементов, превышающим верхнее пороговое значение, определяемое findmethod |
'previous' | Заполняет предыдущим ненулевым значением |
'next' | Заполняет следующим ненулевым значением |
'nearest' | Заполняет ближайшим ненулевым значением |
'linear' | Заполнение с помощью линейной интерполяции соседних значений, не являющихся отклонениями |
'spline' | Заливка с помощью кусочно-кубической интерполяции сплайна |
'pchip' | Заливка с помощью кусочно-кубической интерполяции сплайна с сохранением формы |
'makima' | модифицированная Akima кубическая эрмитовая интерполяция (числовая, duration, и datetime только типы данных) |
Типы данных: double | single | char
findmethod - Метод обнаружения отклонений'median' (по умолчанию) | 'mean' | 'quartiles' | 'grubbs' | 'gesd'Метод обнаружения отклонений, указанный как одно из следующих:
| Метод | Описание |
|---|---|
'median' | Отклонения определяются как элементы с более чем тремя масштабами MAD от медианы. Масштабированный MAD определяется как c*median(abs(A-median(A))), где c=-1/(sqrt(2)*erfcinv(3/2)). |
'mean' | Отклонения определяются как элементы с более чем тремя стандартными отклонениями от среднего значения. Этот метод быстрее, но менее надежен, чем 'median'. |
'quartiles' | Отклонения определяются как элементы более чем 1,5 межквартильных диапазона выше верхнего квартиля (75 процентов) или ниже нижнего квартиля (25 процентов). Этот метод полезен, когда данные в A обычно не распространяется. |
'grubbs' | Отклонения выявляются с помощью теста Груббса, который удаляет одно отклонение на итерацию на основе проверки гипотез. Этот метод предполагает, что данные в A обычно распределяется. |
'gesd' | Отклонения выявляются с помощью обобщенного теста экстремальных отклонений Studentized для отклонений. Этот итеративный метод аналогичен 'grubbs', но может работать лучше, когда существует несколько отклонений, маскирующих друг друга. |
threshold - Пороговые значения процентиляПороги процентиля, определенные как двухэлементный вектор строки, элементы которого находятся в интервале [0,100]. Первый элемент указывает нижний порог процентиля, а второй элемент указывает верхний порог процентиля. Например, пороговое значение [10 90] определяет отклонения как точки ниже 10-го процентиля и выше 90-го процентиля. Первый элемент threshold должно быть меньше второго элемента.
movmethod - Способ перемещения'movmedian' | 'movmean'Способ перемещения для обнаружения отклонений, указанный как одно из следующих:
| Метод | Описание |
|---|---|
'movmedian' | Отклонения определяются как элементы с более чем тремя локальными масштабированными MAD из локальной медианы по длине окна, заданной window. Этот метод также известен как фильтр Хампеля. |
'movmean' | Отклонения определяются как элементы с более чем тремя локальными стандартными отклонениями от локального среднего значения по длине окна, указанной window. |
window - Длина окнаДлина окна, заданная как положительный целочисленный скаляр, двухэлементный вектор положительных целых чисел, скаляр положительной длительности или двухэлементный вектор положительных длительностей.
Когда window является положительным целым скаляром, окно центрировано относительно текущего элемента и содержит window-1 соседние элементы. Если window является четным, то окно центрировано относительно текущего и предыдущего элементов.
Когда window - двухэлементный вектор положительных целых чисел [b f], окно содержит текущий элемент, b элементы назад, и f элементы вперед.
Когда A является расписанием или 'SamplePoints' указан как datetime или duration вектор, window должен иметь тип durationи окна вычисляются относительно точек выборки.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | duration
dim - Размер для работы вдольРазмерность для работы, заданная как целочисленный скаляр. Если значение не указано, то по умолчанию используется первый размер массива, размер которого не равен 1.
Рассмотрим матрицу A.
filloutliers(A,fillmethod,1) заполняет отклонения в соответствии с данными в каждом столбце.
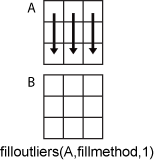
filloutliers(A,fillmethod,2) заполняет отклонения в соответствии с данными в каждой строке.
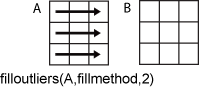
Когда A - таблица или расписание, dim не поддерживается. filloutliers работает по каждой таблице или переменной расписания отдельно.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.
filloutliers(A,'center','mean','ThresholdFactor',4)'SamplePoints' - Выборочные точкиТочки выборки, указанные как пара, разделенная запятыми, состоящая из 'SamplePoints' и вектор. Точки выборки представляют расположение данных по оси X в A, и должны быть отсортированы и содержать уникальные элементы. Выборочные точки не нуждаются в равномерной выборке. Вектором точек выборки по умолчанию является [1 2 3 ...].
Примечание
Эта пара имя-значение не поддерживается, если входными данными являются timetable. В расписаниях всегда используется вектор времени строки в качестве точек выборки. Чтобы использовать различные точки выборки, необходимо отредактировать расписание так, чтобы время строки содержало нужные точки выборки.
Движущиеся окна определяются относительно точек образца. Например, если t является вектором времен, соответствующих входным данным, то filloutliers(rand(1,10),'previous','movmean',3,'SamplePoints',t) имеет окно, представляющее временной интервал между t(i)-1.5 и t(i)+1.5.
Когда вектор точек выборки имеет тип данных datetime или duration, то длина движущегося окна должна иметь тип duration.
Пример: filloutliers([1 100 3 4],'nearest','SamplePoints',[1 2.5 3 4])
Типы данных: single | double | datetime | duration
'DataVariables' - Табличные переменные для работыvartype нижний индексПеременные таблицы для работы, указанные как пара, разделенная запятыми, состоящая из 'DataVariables' и один из вариантов в этой таблице. 'DataVariables' значение указывает переменные входной таблицы для заполнения. Другие переменные в таблице, не указанные 'DataVariables' пройти на выход без работы.
| Выбор | Описание | Примеры |
|---|---|---|
| Имя переменной | Вектор символов или скалярная строка, задающая имя переменной одной таблицы |
|
| Вектор имен переменных | Массив ячеек символьных векторов или строковый массив, где каждый элемент является именем переменной таблицы |
|
| Скаляр или вектор переменных индексов | Скаляр или вектор индексов табличных переменных |
|
| Логический вектор | Логический вектор, элементы которого соответствуют переменной таблицы, где |
|
| Дескриптор функции | Дескриптор функции, принимающий переменную таблицы в качестве входного значения и возвращающий логический скаляр |
|
vartype нижний индекс | Подстрочный индекс таблицы, созданный |
|
Пример: filloutliers(A,'previous','DataVariables',["Var1" "Var2" "Var4"])
'ThresholdFactor' - Пороговый коэффициент обнаруженияПороговый коэффициент обнаружения, указанный как пара, разделенная запятыми, состоящая из 'ThresholdFactor' и неотрицательный скаляр.
Для методов 'median' и 'movmedian'пороговый коэффициент обнаружения заменяет число масштабированных MAD, которое по умолчанию равно 3.
Для методов 'mean' и 'movmean'пороговый коэффициент обнаружения заменяет количество стандартных отклонений от среднего значения, которое по умолчанию равно 3.
Для методов 'grubbs' и 'gesd', пороговый коэффициент обнаружения является скаляром в диапазоне от 0 до 1. Значения, близкие к 0, приводят к меньшему числу отклонений, а значения, близкие к 1, приводят к большему числу отклонений. Пороговый коэффициент обнаружения по умолчанию равен 0,05.
Для 'quartiles' пороговый коэффициент обнаружения заменяет количество межквартильных диапазонов, которое по умолчанию равно 1,5.
Эта пара имя-значение не поддерживается, если указан метод 'percentiles'.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
'MaxNumOutliers' - Максимальное число отклоненийМаксимальное число отклонений, для 'gesd' только метод, указанный как разделенная запятыми пара, состоящая из 'MaxNumOutliers' и положительный скаляр. 'MaxNumOutliers' значение указывает максимальное количество отклонений, возвращаемых 'gesd' способ. Например, filloutliers(A,'linear','gesd','MaxNumOutliers',5) возвращает не более пяти отклонений.
Значение по умолчанию для 'MaxNumOutliers' является целым числом, ближайшим к 10 процентам от числа элементов в A. Установка большего значения для максимального числа отклонений может обеспечить обнаружение всех отклонений, но за счет снижения вычислительной эффективности.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
'OutlierLocations' - Известный показатель отклоненияИзвестный индикатор отклонения, указанный как пара, разделенная запятыми, состоящая из 'OutlierLocations' и логический вектор, матрица или многомерный массив того же размера, что и A. Известные элементы индикатора отклонения могут быть true чтобы указать отклонение в соответствующем местоположении A или false в противном случае. Определение 'OutlierLocations' отключает метод обнаружения отклонений по умолчанию и использует только элементы известного индикатора отклонений для определения отклонений.
'OutlierLocations' пара имя-значение не может быть указана, когда findmethod указывается.
Продукция TF совпадает с 'OutlierLocations' значение.
Типы данных: logical
B - Заполненный массив отклоненийЗаполненный массив отклонений, возвращаемый как вектор, матрица, многомерный массив, таблица или расписание. Элементы B такие же, как у A, но со всеми отклонениями, замененными согласно fillmethod.
Типы данных: double | single | table | timetable
TF - Индикатор отклоненияИндикатор отклонения, возвращаемый как вектор, матрица или многомерный массив. Элемент TF является true когда соответствующий элемент A является отклонением и false в противном случае. TF имеет тот же размер, что и A.
Типы данных: logical
L - Нижний порогНижний порог, используемый методом обнаружения отклонений, возвращаемый как скаляр, вектор, матрица, многомерный массив, таблица или расписание. Например, меньшее значение метода обнаружения отклонений по умолчанию - три масштабированных MAD ниже медианы входных данных. L имеет тот же размер, что и A во всех размерах, за исключением рабочего размера, где длина равна 1.
Типы данных: double | single | table | timetable
U - Верхний порогВерхний порог, используемый методом обнаружения отклонений, возвращаемый как скаляр, вектор, матрица, многомерный массив, таблица или расписание. Например, верхним значением метода обнаружения отклонений по умолчанию является три масштабированных MAD выше медианы входных данных. U имеет тот же размер, что и A во всех размерах, за исключением рабочего размера, где длина равна 1.
Типы данных: double | single | table | timetable
C - Значение центраЗначение центра, используемое методом обнаружения отклонений, возвращаемое в виде скаляра, вектора, матрицы, многомерного массива, таблицы или расписания. Например, центральным значением метода обнаружения отклонений по умолчанию является медиана входных данных. C имеет тот же размер, что и A во всех размерах, за исключением рабочего размера, где длина равна 1.
Типы данных: double | single | table | timetable
Для вектора случайной величины A, составленного из N скалярных наблюдений, среднее абсолютное отклонение (MAD) определяется как
(A) |)
для i = 1,2,...,N.
Масштабированный MAD определяется как c*median(abs(A-median(A))) где c=-1/(sqrt(2)*erfcinv(3/2)).
Примечания и ограничения по использованию:
'percentiles', 'grubs', и 'gesd' методы не поддерживаются.
'movmedian' и 'movmean' методы не поддерживают высокие расписания.
'SamplePoints' и 'MaxNumOutliers' пары имя-значение не поддерживаются.
Значение 'DataVariables' не может быть дескриптором функции.
Расчет filloutliers(A,fillmethod), filloutliers(A,fillmethod,'median',…) или filloutliers(A,fillmethod,'quartiles',…) вдоль первого размера поддерживается только тогда, когда A - вектор высокого столбца.
Синтаксисы filloutliers(A,'spline',…) и filloutliers(A,'makima',…) не поддерживаются.
Дополнительные сведения см. в разделе Массивы Tall.
Примечания и ограничения по использованию:
'movmean' и 'movmedian' методы обнаружения отклонений не поддерживают входные данные расписания, datetime 'SamplePoints' значения или длительность 'SamplePoints' значения.
Только 'center', 'clip'и поддерживаются числовые скалярные методы для заполнения отклонений, когда входные данные являются расписанием или когда 'SamplePoints' значение имеет тип datetime или duration.
Для использования 'spline' и 'pchip' необходимо включить поддержку массивов переменного размера.
Строковые и символьные вводы должны быть постоянными.
'makima' параметры не поддерживаются.
Очистить данные об отклонениях | fillmissing | ismissing | isoutlier | rmoutliers
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.