Exponenta Banner
exponenta event banner

spdiags

Извлечение ненулевых диагоналей и создание разреженных полосовых и диагональных матриц

свернуть все на странице

Синтаксис

Bout = spdiags (A)
[Bout, id] = spdiags (A)
Bout = spdiags (A, d)
S = spdiags (Bin, d, m, n)
S = spdiags (Bin, d, A)

Описание

пример

Bout = spdiags(A) извлекает ненулевые диагонали из mоколо-n матрица A и возвращает их в виде столбцов в min(m,n)около-p матрица Bout, где p - число ненулевых диагоналей.

пример

[Bout,id] = spdiags(A) также возвращает диагональные числа id для ненулевых диагоналей в A. Размер Bout является min(m,n)около-length(id).

пример

Bout = spdiags(A,d) извлекает диагонали в A указано d и возвращает их в виде столбцов min(m,n)около-length(d) матрица Bout.

пример

S = spdiags(Bin,d,m,n) создает mоколо-n разреженная матрица S взяв столбцы Bin и размещение их вдоль диагоналей, указанных d.

пример

S = spdiags(Bin,d,A) заменяет диагонали в A указано d со столбцами Bin.

Примеры

свернуть все

Открыть сценарий в реальном времени

Создайте тридиагональную матрицу с помощью трех векторов, измените некоторые диагонали матрицы, а затем извлеките диагонали.

Создайте вектор 9 на 1, а затем с помощью вектора создайте тридиагональную матрицу. Просмотрите элементы матрицы.

n = 9;
e = ones(n,1);
A = spdiags([e -2*e e],-1:1,n,n);
full(A)
ans = 9×9

    -2     1     0     0     0     0     0     0     0
     1    -2     1     0     0     0     0     0     0
     0     1    -2     1     0     0     0     0     0
     0     0     1    -2     1     0     0     0     0
     0     0     0     1    -2     1     0     0     0
     0     0     0     0     1    -2     1     0     0
     0     0     0     0     0     1    -2     1     0
     0     0     0     0     0     0     1    -2     1
     0     0     0     0     0     0     0     1    -2

Измените значения на главном (d = 0) диагональ A.

Bin = abs(-(n-1)/2:(n-1)/2)';
d = 0;
A = spdiags(Bin,d,A);
full(A)
ans = 9×9

     4     1     0     0     0     0     0     0     0
     1     3     1     0     0     0     0     0     0
     0     1     2     1     0     0     0     0     0
     0     0     1     1     1     0     0     0     0
     0     0     0     1     0     1     0     0     0
     0     0     0     0     1     1     1     0     0
     0     0     0     0     0     1     2     1     0
     0     0     0     0     0     0     1     3     1
     0     0     0     0     0     0     0     1     4

Наконец, восстановите диагонали A в виде столбцов в матрице.

Bout = spdiags(A);
full(Bout)
ans = 9×3

     1     4     0
     1     3     1
     1     2     1
     1     1     1
     1     0     1
     1     1     1
     1     2     1
     1     3     1
     0     4     1
Открыть сценарий в реальном времени

Извлеките ненулевые диагонали матрицы и проверьте формат вывода spdiags.

Создайте матрицу, содержащую смесь ненулевых и нулевых диагоналей.

A = [0     5     0    10     0     0
     0     0     6     0    11     0
     3     0     0     7     0    12
     1     4     0     0     8     0
     0     2     5     0     0     9];

Извлеките ненулевые диагонали из матрицы. Укажите два выхода для возврата диагональных чисел.

[Bout,d] = spdiags(A)
Bout = 5×4

     0     0     5    10
     0     0     6    11
     0     3     7    12
     1     4     8     0
     2     5     9     0


d = 4×1

    -3
    -2
     1
     3

Столбцы первого вывода Bout содержат ненулевые диагонали A. Второй выход d перечисляет индексы ненулевых диагоналей A. Самая длинная ненулевая диагональ в A в столбце 3 Bout. Чтобы дать все столбцы Bout той же длины, другие ненулевые диагонали A добавить дополнительные нули к соответствующим столбцам в Bout. Для mоколо-n матрицы с m < n, правила:

  • Для ненулевых диагоналей ниже основной диагонали A, дополнительные нули добавляются в вершинах столбцов (как в первых двух столбцах Bout).

  • Для ненулевых диагоналей над главной диагональю A, дополнительные нули добавляются в нижней части столбцов (как в последнем столбце Bout).

spdiags подушки Bout с нулями таким образом, даже если самая длинная диагональ не возвращается в Bout.

Открыть сценарий в реальном времени

Создайте случайную матрицу 5 на 5.

A = randi(10,5,5)
A = 5×5

     9     1     2     2     7
    10     3    10     5     1
     2     6    10    10     9
    10    10     5     8    10
     7    10     9    10     7

Извлеките основную диагональ и первые диагонали над и под ней.

d = [-1 0 1];
Bout = spdiags(A,d)
Bout = 5×3

    10     9     0
     6     3     1
     5    10    10
    10     8    10
     0     7    10

Попробуйте извлечь пятую супердиагональную (d = 5). Поскольку A имеет только четыре супердиагонали, spdiags возвращает диагональ как все нули той же длины, что и основная (d = 0) диагональ.

B5 = spdiags(A,5)
B5 = 5×1

     0
     0
     0
     0
     0
Открыть сценарий в реальном времени

Изучите, как spdiags создает диагонали, когда столбцы входной матрицы длиннее диагоналей, которые они заменяют.

Создайте матрицу 6 на 7 чисел от 1 до 6.

Bin = repmat((1:6)',[1 7])
Bin = 6×7

     1     1     1     1     1     1     1
     2     2     2     2     2     2     2
     3     3     3     3     3     3     3
     4     4     4     4     4     4     4
     5     5     5     5     5     5     5
     6     6     6     6     6     6     6

Использовать spdiags для создания квадратной матрицы 6 на 6 с несколькими столбцами Bin в виде диагоналей. Поскольку некоторые диагонали имеют только один или два элемента, существует несоответствие в размерах между столбцами в Bin и диагонали в A.

d = [-4 -2 -1 0 3 4 5];
A = spdiags(Bin,d,6,6);
full(A)
ans = 6×6

     1     0     0     4     5     6
     1     2     0     0     5     6
     1     2     3     0     0     6
     0     2     3     4     0     0
     1     0     3     4     5     0
     0     2     0     4     5     6

Каждый из столбцов в Bin имеет шесть элементов, но только главную диагональ в A имеет шесть элементов. Поэтому все остальные диагонали в A усечение элементов в столбцах Bin чтобы они умещались на выбранных диагоналях:

Путь spdiags усечение диагоналей зависит от размера mоколо-n матрица A. При m≥n поведение выглядит следующим образом:

  • Диагонали под главной диагональю берут сначала элементы от вершин колонн.

  • Диагонали над главной диагональю берут сначала элементы из низов колонн.

Такое поведение меняется на обратное, когда m < n:

A = spdiags(Bin,d,5,6);
full(A)
ans = 5×6

     1     0     0     1     1     1
     2     2     0     0     2     2
     3     3     3     0     0     3
     0     4     4     4     0     0
     5     0     5     5     5     0

  • Диагонали над главной диагональю берут сначала элементы от вершин колонн.

  • Диагонали под главной диагональю берут сначала элементы из низов колонн.

Входные аргументы

свернуть все

Входная матрица. Эта матрица обычно (но не обязательно) разрежена.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного номера: Да

Диагональные числа, заданные как скаляр или вектор положительных целых чисел. Диагональные числа соответствуют тем же правилам, что и diag:

  • d < 0 находится ниже основной диагонали и удовлетворяет d >= -(m-1).

  • d = 0 является главной диагональю.

  • d > 0 находится над главной диагональю и удовлетворяет d <= (n-1).

Один mоколо-n матрица A имеет (m + n - 1) диагонали. Эти диагонали указаны в векторе d использование индексов из -(m-1) кому (n-1). Например, если A равно 5 на 6, имеет 10 диагоналей, которые указаны в векторе d используя индексы -4, -3,... 4, 5. Следующая диаграмма иллюстрирует эту диагональную нумерацию.

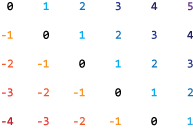
Если задать диагональ, лежащую за пределами A (например, d = 7 в примере выше), то spdiags возвращает эту диагональ как все нули.

Пример: spdiags(A,[3 5]) извлекает третью и пятую диагонали из A.

Диагональные элементы, заданные как матрица. Эта матрица обычно (но не обязательно) заполнена. spdiags использует столбцы Bin для замены указанных диагоналей в A. Если запрошенный размер выходного сигнала равен mоколо-n, то Bin должен иметь min(m,n) столбцы.

С синтаксисом S = spdiags(Bin,d,m,n), если столбец Bin имеет больше элементов, чем диагональ, которую он заменяет, и m >= n, то spdiags принимает элементы супердиагоналей из нижней части колонны Binи элементы субдиагоналей из верхней части столбца Bin. Однако, если m < n , то супердиагонали находятся из верхней части столбца Binи субдиагонали из нижней части. Пример этого поведения см. в разделе Столбцы и диагонали различных размеров.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного номера: Да

Размеры, указанные как неотрицательные скалярные целые числа. spdiags использует эти входные данные для определения размера создаваемой матрицы.

Пример: spdiags(Bin,d,300,400) создает матрицу 300 на 400 со столбцами B размещены вдоль указанных диагоналей d.

Выходные аргументы

свернуть все

Диагональные элементы, возвращаемые в виде полной матрицы. Столбцы Bout содержат диагонали, извлеченные из A. Любые элементы Bout соответствующие позициям за пределами A имеют нулевое значение.

Диагональные числа, возвращаемые в виде вектора столбца. Посмотрите d описание нумерации диагоналей.

Выходная матрица. S принимает одну из двух форм:

  • С S = spdiags(Bin,d,A), указанные диагонали в A заменены столбцами в Bin создать S.

  • С S = spdiags(Bin,d,m,n), mоколо-n разреженная матрица S образуется взятием колонн Bin и размещение их вдоль диагоналей, указанных d.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™

.

См. также

|

Представлен до R2006a

Документация MATLAB

Поддержка