Куб определяется восемью вершинами, образующими шесть сторон. На этом рисунке показаны координаты x, y и z вершин, определяющих куб, в котором стороны составляют одну единицу длины.
Если в качестве векторов задаются аргументы координат x, y и z, они визуализируются как один многоугольник с точками, соединенными последовательно. Если аргументами являются матрицы, MATLAB ® рисует один многоугольник на столбец, создавая один фрагмент с несколькими гранями. Эти грани не обязательно должны быть соединены и могут быть самопересекающимися.
Можно также задать координаты каждой уникальной вершины и порядок их соединения с образованием граней. Примеры в этом разделе иллюстрируют оба метода.
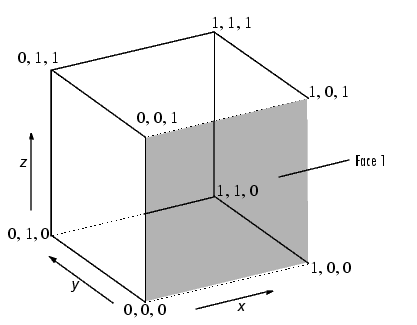
Каждая из шести граней имеет четыре вершины. Поскольку не нужно закрывать каждый многоугольник (т.е. первая и последняя вершины не должны быть одинаковыми), можно определить этот куб с помощью матрицы 4 на 6 для каждой из координат x -, y - и z.
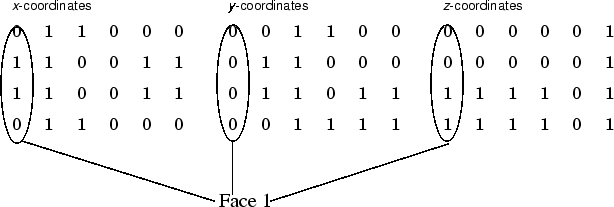
Каждый столбец матриц определяет другую грань. Хотя имеется только восемь вершин, для определения всех шести граней необходимо указать 24 вершины. Поскольку каждая грань имеет общие вершины с четырьмя другими гранями, можно более эффективно определить сегмент, определив каждую вершину только один раз, а затем указав порядок соединения этих вершин для формирования каждой грани. Участок Vertices и Faces свойства определяют исправления только таким образом.
Эти матрицы определяют куб с помощью
Vertices и Faces.
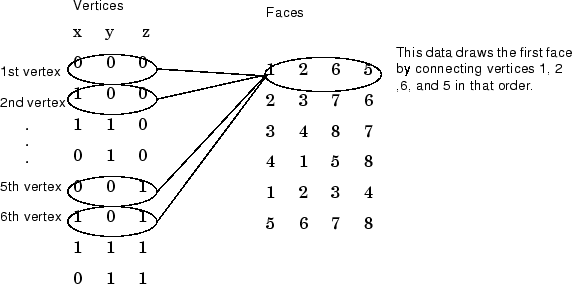
Использование техники вершин/граней может сэкономить значительный объем памяти компьютера, когда патчи содержат большое количество граней. Этот метод требует формального patch синтаксис функции, который влечет за собой назначение значений Vertices и Faces явно. Например,
patch('Vertices',vertex_matrix,'Faces',faces_matrix)
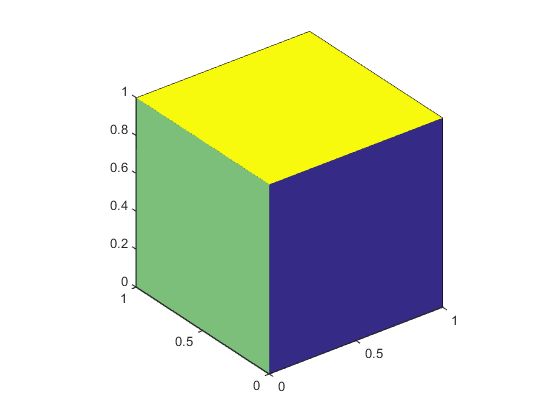
Поскольку высокоуровневый синтаксис не назначает автоматически цвета граней или кромок, необходимо задать соответствующие свойства для создания фрагментов с цветами, отличными от цвета белой грани и цвета черной кромки по умолчанию.
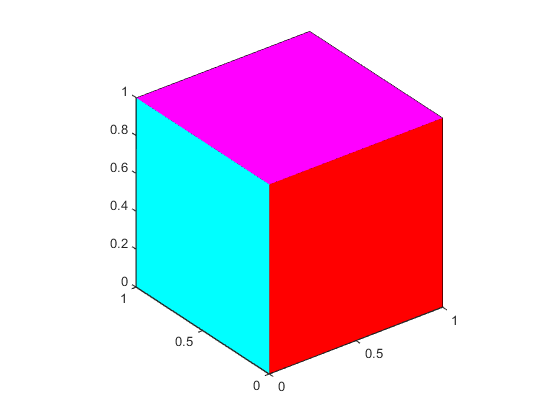
Цвет плоской грани является результатом задания одного цвета для каждой грани. Например, используя технику вершин/граней и FaceVertexCData для определения цвета этот оператор задает один цвет на грань и задает FaceColor свойство для flat.
vert = [0 0 0;1 0 0;1 1 0;0 1 0;0 0 1;1 0 1;1 1 1;0 1 1];
fac = [1 2 6 5;2 3 7 6;3 4 8 7;4 1 5 8;1 2 3 4;5 6 7 8];
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',hsv(6),'FaceColor','flat')
Отрегулируйте оси:
view(3) axis vis3d
Потому что truecolor указан с помощью FaceVertexCData имеет тот же формат, что и карта цветов MATLAB (т.е. массив значений RGB n-by-3), в этом примере используется hsv colormap для создания шести цветов, необходимых для плоского затенения.
Чтобы сопоставить цвета граней с текущей картой цветов, назначьте массиву n-by-1 FaceVertexCData свойство:
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',(1:6)','FaceColor','flat')Отрегулируйте оси:
view(3) axis vis3d
Интерполированный цвет грани означает, что цвета вершин каждой грани определяют переход цвета от одной вершины к следующей. Для интерполяции цветов между вершинами необходимо указать цвет для каждой вершины и задать FaceColor свойство для interp.
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',hsv(8),'FaceColor','interp')
Отрегулируйте оси:
view(3) axis vis3d
создает куб с каждой гранью, окрашенной путем интерполяции цветов вершин.
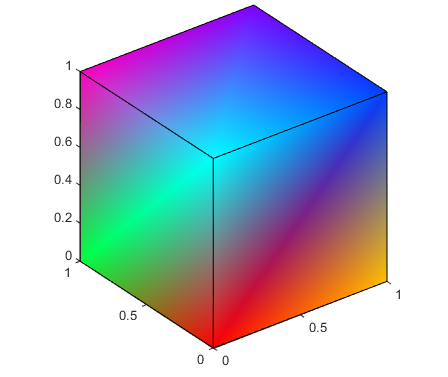
Чтобы определить ту же окраску, используя x, y, z, c техника, c должен быть множеством m на n на 3, где размеры x, y, и z составляют m на n.
На этой диаграмме показано соответствие между FaceVertexCData и CData свойства.

Как данные исправления относятся к карте цветов, более подробно рассматриваются методы раскраски.