Можно экспортировать модели в рабочую область для работы с ними в MATLAB ®.
В браузере модели или любом узле модели выберите «Файл» > «Экспорт моделей». Откроется диалоговое окно Экспорт моделей (Export Models).
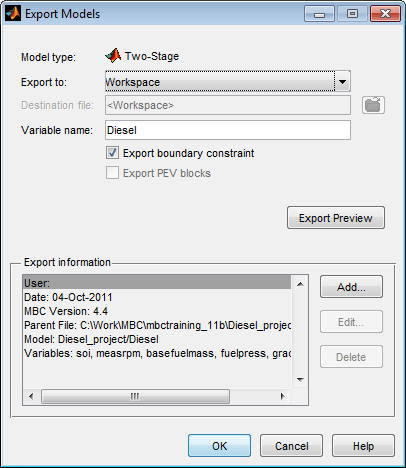
Выбрать Workspace из списка Экспорт в (Export to).
При необходимости измените имя переменной.
При наличии граничной зависимости она экспортируется, если не снять флажок Экспортировать граничную зависимость (Export boundary constraint).
(Необязательно) Щелкните Предварительный просмотр экспорта (Export Preview), чтобы проверить модели, выбранные для экспорта:
Из узла плана тестирования экспортируются все модели отклика в плане тестирования (при условии, что выбраны лучшие модели для них всех) или модели «точка за точкой» (если все локальные модели являются несколькими моделями).
Из локальной модели экспортируются все локальные модели как двухточечная модель.
Из других узлов модели экспортируется только текущая модель.
В поле Тип модели (Model type) диалогового окна Экспорт моделей (Export Models) отображается тип экспортируемой модели: двухступенчатый, двухточечный или другой тип модели.
(Необязательно) Нажмите кнопку «Добавить», чтобы добавить комментарий к информации об экспорте.
Нажмите кнопку ОК, чтобы экспортировать модели в рабочую область.
После экспорта модели в рабочую область можно выполнить следующие действия.
Оцените модель.
Оцените дисперсию ошибки прогнозирования (ПЭВ).
Вычислите граничную модель.
Рассчитайте доверительные интервалы для прогнозирования модели.
Экспортированные модели отображаются в рабочей области как xregstatsmodel или mbcPointByPointModel объект или массив ячеек моделей. Для вычисления используются одни и те же команды xregstatsmodel или mbcPointByPointModel модели.
При экспорте группы моделей панель инструментов экспортирует массив ячеек моделей. Порядок аргументов в массиве ячеек {1 to n} соответствует порядку модели сверху вниз в дереве модели в браузере модели.
Например, при экспорте модели в рабочую область как MyModel и модель имеет четыре входных фактора, оцените модель в точке, как показано здесь:
Y = MyModel([3.7,89.55,-0.005,1]);
При создании векторов столбцов p1,p2,p3,p4 (равной длины) для каждого входного коэффициента можно вычислить модель, чтобы получить вывод вектора столбца:
Y = MyModel([p1,p2,p3,p4]);
Порядок аргументов слева направо соответствует порядку ввода данных сверху вниз на виде «План тестирования» в браузере модели.
Входные и выходные данные для оценки модели MATLAB представлены в единицах естественного проектирования, а не в кодированных единицах.
Можно вычислить ПЭВ для модели с помощью команды:
[pev, y] = pev(MyModel, [x1 x2 x3])
Можно использовать один или два аргумента следующим образом:
[p] = pev(x) дает pev в x.
[p,y] = pev(x) дает pev в x и оценка модели на x.
Дополнительные сведения см. в разделе xregstatsmodel.
Использовать predint для оценки доверительных интервалов модели:
Interval = predint(StatsModel,X,Level);
Level вычисляют доверительный интервал предсказаний относительно прогнозируемого значения. Значение по умолчанию для Level является 99. Interval является Nx2 массив, где первый столбец является нижней границей, а второй столбец является верхней границей.Доверительный интервал задается:
upperbound = y + t*sqrt(pev) lowerbound = y - t*sqrt(pev)
где y является прогнозом модели, и t - соответствующий процентиль t-статистики с df = nObs-1 степеней свободы. Панель инструментов вычисляет это с помощью функции Toolbox™ статистики и машинного обучения tinv следующим образом:
t = tinv(p,v)
p = confidence level, например, 95%
v = degrees of freedom (n-1)
t = tinv(1-alpha/2, df)
где alpha = 0.05 для 95% доверительных интервалов.
Можно использовать функцию ceval для вычисления граничной зависимости, экспортируемой в рабочее пространство. Например, если экспортируемая модель M, то
ceval(M, X)
M в точках, заданных матрицей X. Значения меньше 0 находятся внутри границы. См. раздел Анализ типов граничных моделей.Например, при экспорте нескольких ответов из плана тестирования в виде массива ячеек с именем modeltutorial, введя в командной строке следующее, вычисляет граничную модель для первого ответа {1} в точке, где все четыре входа равны 0:
ceval(modeltutorial{1}, [0,0,0,0])
Модели ответа находятся в нисходящем порядке в дереве модели. Например, {1} является верхней моделью в дереве узла плана тестирования. [0,0,0,0] - матрица входных значений, где порядок аргументов слева направо соответствует порядку ввода сверху вниз в редакторе границ или виде плана тестирования в браузере модели, например spk, load, rpm и afr.
Можно быстро проверить количество входных данных модели следующим образом:
nfactors(modeltutorial{1})
Можно щелкнуть точку в редакторе границ (на видах 1-D, 2-D и 3-D), чтобы проверить имена входных данных и получить примерные входные значения для вычисления в рабочем пространстве, например:
ceval (modeltutorial{1},[25, 0.64, 5000, 14.43])
ans = 3.0284e-004
Расстояние граничной зависимости 0 означает, что точка находится на границе, отрицательные значения находятся внутри зависимости, а положительные значения находятся снаружи. Диапазон обычно [-1,1], но не всегда, и приблизительно линейный. Как и информационные критерии, это только сравнение, которое является значимым (точка x имеет большее расстояние, чем точка y), а не абсолютное значение.
Дополнительные сведения см. в разделе xregstatsmodel.