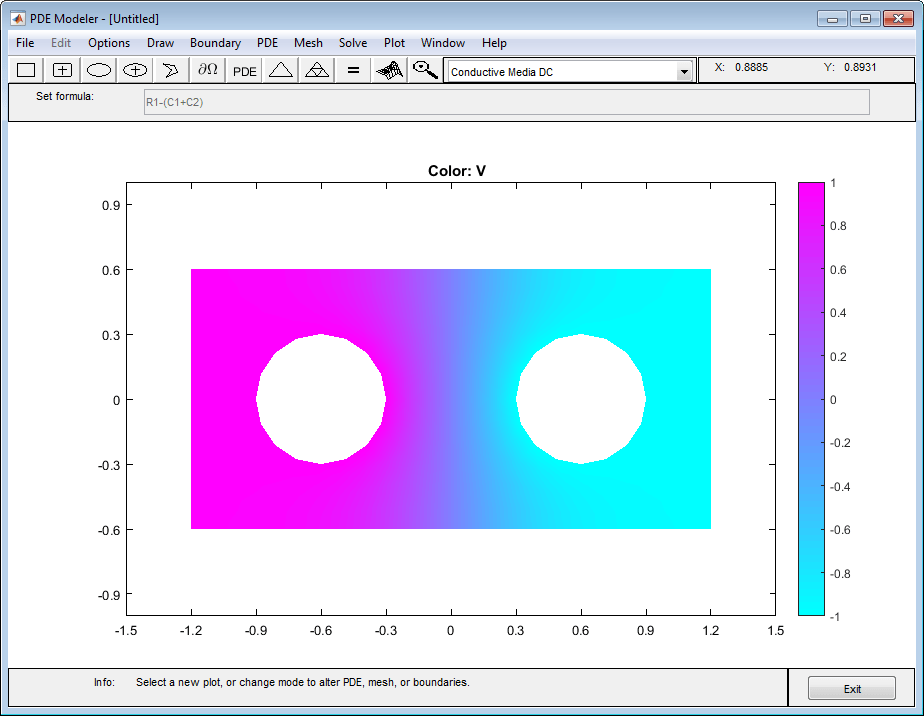
Два круглых металлических проводника размещены на пропитанной рассолом блоттинговой бумаге, которая служит плоским тонким проводником. Физическая модель для этой задачи состоит из уравнения Лапласа
- ∇ · (σ ∇ V) = 0
для электрического потенциала V и этих граничных условий:
V = 1 на левом круговом проводнике
V = -1 на правом круговом проводнике
естественное граничное условие Неймана на внешних границах
Проводимость δ = 1.
Чтобы решить это уравнение в приложении PDE Modeler, выполните следующие действия:
Моделирование геометрии: построение прямоугольника с углами (-1,2, -0,6), (1,2, -0,6), (1,2,0,6) и (-1,2,0,6) и двумя окружностями с радиусом 0,3 и центрами (-,6,0) и (0,6,0). Прямоугольник представляет блоттинговую бумагу, а круги - проводники.
pderect([-1.2 1.2 -0.6 0.6]) pdecirc(-0.6,0,0.3) pdecirc(0.6,0,0.3)
Моделирование геометрии путем ввода R1-(C1+C2) в поле Задать формулу.
Установите режим приложения «Conductive Media DC».
Задайте граничные условия. Для этого переключитесь в граничный режим, выбрав «Граница» > «Граничный режим». Используйте клавиши SHIFT + щелчок для выбора нескольких границ. Затем выберите «Граница» > «Задать граничные условия».
Для прямоугольника используйте граничное условие Неймана с g = 0 и q = 0.
Для левой окружности используйте граничное условие Дирихле с h = 1 и r = 1.
Для правой окружности используйте граничное условие Дирихле с h = 1 и r = -1.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Определить sigma = 1 и q = 0.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».
Уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».
Улучшите качество треугольника, выбрав меню «Сеть» > «Сгиб сетки».
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов. Результирующий потенциал равен нулю вдоль оси y, которая для данной задачи является вертикальной линией антисимметрии.
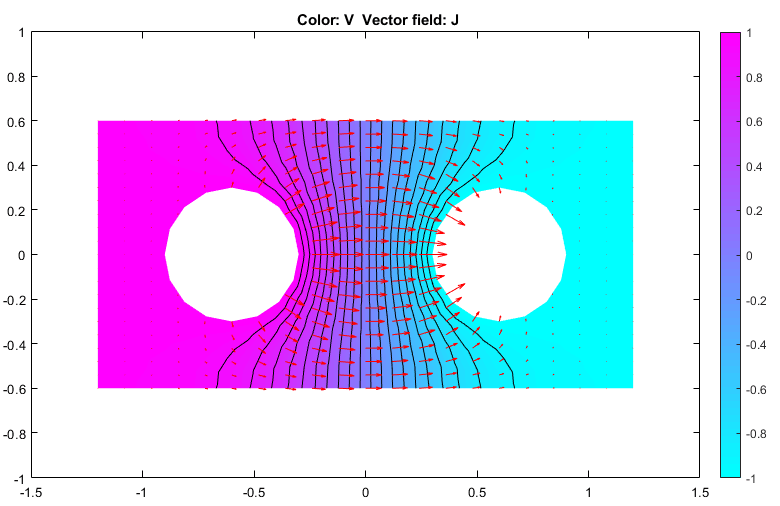
Постройте график плотности тока J. Для этого:
Выберите «Печать» > «Параметры».
В открывшемся диалоговом окне выберите параметры «Цвет», «Контур» и «Стрелки».
Задайте для параметра «Стрелки» значение current density.
Ток течет, как и ожидалось, от проводника с положительным потенциалом к проводнику с отрицательным потенциалом. Проводимость λ изотропна, а эквипотенциальные линии ортогональны текущим линиям.