Найдите электростатический потенциал в заполненном воздухом кольцевом четырехугольнике с помощью приложения PDE Modeler. Для этого примера используйте следующие параметры:
Внутренняя квадратная сторона 0,2 м
Внешняя квадратная сторона 0,5 м
Электростатический потенциал на внутренней границе составляет 1000V
Электростатический потенциал на внешней границе составляет 0V
PDE, регулирующий эту задачу, - уравнение Пуассона
- ∇ · (ε ∇ V) = ρ.
В приложении PDE Modeler используется относительная диэлектрическая проницаемость αr = start/α0, где α0 - абсолютная диэлектрическая диэлектрическая проницаемость вакуума (8 854· 10-12 фарад/метр). Относительная диэлектрическая проницаемость воздуха составляет 1,00059. Следует отметить, что коэффициент диэлектрической проницаемости не влияет на результат в этом примере, пока коэффициент является постоянным.
Предполагая, что в области нет заряда, можно упростить уравнение Пуассона до уравнения Лапласа,
ΔV = 0.
Здесь граничными условиями являются граничные условия Дирихле V = 1000 на внутренней границе и V = 0 на внешней границе.
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие действия:
Нарисуйте следующие два квадрата.
pderect([-0.1 0.1 -0.1 0.1]) pderect([-0.25 0.25 -0.25 0.25])
Установите пределы по осям X и Y в значение [-0.3 0.3]. Для этого выберите Опции (Options) > Границы осей (Axes Limits) и задайте соответствующие диапазоны. Затем выберите «Параметры» > «Оси равны».
Моделирование кадра путем ввода SQ2-SQ1 в поле Задать формулу.
Установите режим приложения «Электростатика».
Задайте граничные условия. Для этого переключитесь в граничный режим, выбрав «Граница» > «Граничный режим». Используйте клавиши SHIFT + щелчок для выбора нескольких границ. Затем выберите «Граница» > «Задать граничные условия».
Для внутренних границ используйте граничное условие Дирихле с h = 1 и r = 1000.
Для внешних границ используйте граничное условие Дирихле с h = 1 и r = 0.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Определить epsilon = 1 и rho = 0.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов.
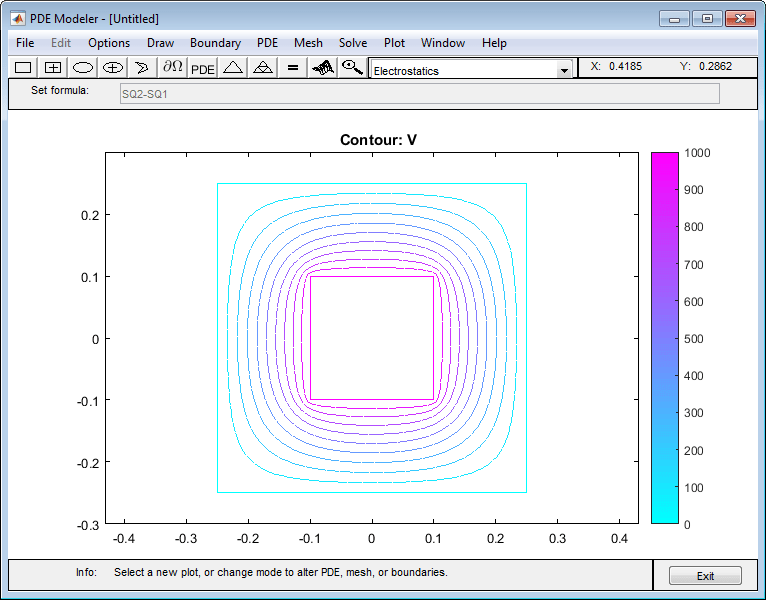
Постройте график эквипотенциальных линий, используя контурный график. Для этого выберите «Печать» > «Параметры» и выберите график горизонталей в открывшемся диалоговом окне.
Повысьте точность решения, уточнив сетку близко к входящим углам, где градиенты крутые. Для этого выберите «Решение» > «Параметры». Выберите «Адаптивный режим», используйте метод выбора «Худшие треугольники» и установите максимальное количество треугольников равным 500. Выберите «Сетка» > «Уточнить сетку».
Решите PDE с помощью уточненной сетки. Для отображения эквипотенциальных линий при каждом 100-м вольте выберите «Печать» > «Параметры» и введите 0:100:1000 в поле Уровни горизонталей.