Решите 3-D параболическую задачу PDE, сократив задачу до 2-D с помощью преобразования координат. В этом примере используется приложение PDE Modeler. Для получения информации о решении в командной строке см. раздел Распределение тепла в круговом цилиндрическом стержне.
Рассмотрим цилиндрический радиоактивный стержень. Тепло непрерывно добавляют на левом конце стержня, в то время как правый конец поддерживают при постоянной температуре. На внешней границе происходит теплообмен с окружающей средой путем переноса. При этом тепло равномерно вырабатывается во всем стержне за счет радиоактивных процессов. Допущение, что начальная температура равна нулю, приводит к следующему уравнению:
q
В данном случае, start, C и k - плотность, тепловая емкость и теплопроводность материала, u - температура, q - тепло, генерируемое в стержне.
Поскольку задача осесимметрична, удобно записать это уравнение в цилиндрической системе координат.
k∂u∂z) = q
Здесь r, startи z являются тремя координатными переменными цилиндрической системы. Потому что проблема осесимметрична,
Это цилиндрическая задача, и Toolbox™ дифференциального уравнения в частных производных требует, чтобы уравнения находились в декартовых координатах. Чтобы преобразовать уравнение в декартовы координаты, сначала умножьте обе стороны уравнения на r:
= qr
Затем определите r как y и z как x:
qy
В этом примере используются следующие параметры:
Плотность, start= 7800 кг/м3
Тепловая мощность, C = 500 Вт· с/кг· ºC
Теплопроводность, k = 40 Вт/мºС
Радиоактивный источник тепла, q = 20000 W/m3
Температура в правом конце, T_right = 100 ° C
Тепловой поток в левом конце, HF_left = 5000 W/m2
Температура окружающей среды на внешней границе, T_outer = 100 ° C
Коэффициент теплопередачи, h_outer = 50 Вт/м2· ºC
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие действия:
Моделируйте стержень как прямоугольник с углами в (-,5,0), (1,5,0), (1,5,0,2) и (-,5,0,2). Здесь ось x представляет направление z, а ось y представляет направление r.
pderect([-1.5,1.5,0,0.2])
Задайте граничные условия. Для этого дважды щелкните границы, чтобы открыть диалоговое окно «Граничное условие». Приложение PDE Modeler требует граничных условий в определенной форме. Таким образом граничные условия Неймана должны быть в +qu=g, и граничные условия Дирихле должен быть в форме hu = r. Кроме того, поскольку обе стороны уравнения умножены на r = y, умножьте коэффициенты для граничных условий на y.
Для левого конца используйте условие Неймана 5000. Определитьg = 5000*y и q = 0.
Для правого конца используйте условие Дирихле u = T_right = 100. Определить h = 1 и r = 100.
Для внешней границы используйте условие Неймана (100 − u ). Определитьg = 50*y*100 и q = 50*y.
Ось цилиндра r = 0 не является границей в исходной задаче, но в 2-D обработке она стала единицей. Используйте искусственное граничное условие Неймана для оси, . Определить g = 0 и q = 0.
Задайте коэффициенты, выбрав PDE (PDE) > PDE Specification (спецификация PDE) или нажав кнопку PDE (PDE) на панели инструментов. Уравнение тепла является параболическим уравнением, поэтому выберите параболический тип PDE. Поскольку обе стороны уравнения умножены на r = y, умножьте коэффициенты на y и введите следующие значения: c = 40*y, a = 0, f = 20000*y, и d = 7800*500*y.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».
Установите начальное значение 0, время решения - 20000 секунд, и вычислите решение каждые 100 секунд. Для этого выберите «Решение» > «Параметры». В диалоговом окне «Параметры решения» задайте время равным 0:100:20000, и u (t0) в0.
Решите уравнение, выбрав команду Решить (Solve) > Решить PDE (Solve PDE) или нажав кнопку = на панели инструментов.
Постройте график решения, используя цвет и контурный график. Для этого выберите «Печать» > «Параметры» и выберите цвета и контурные графики в открывшемся диалоговом окне.
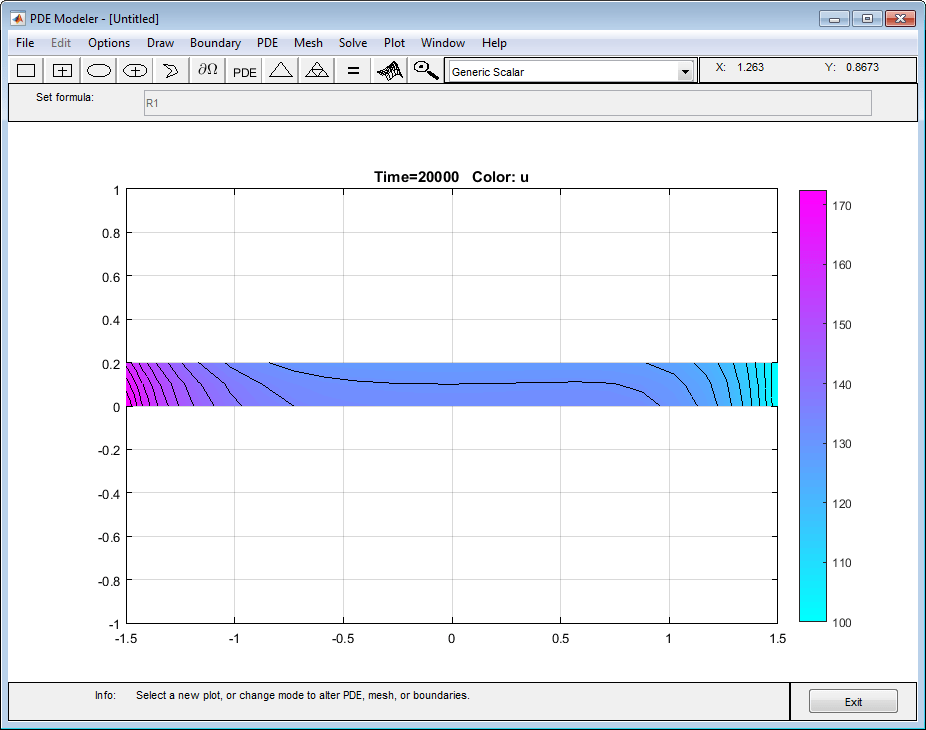
Можно исследовать решение, изменяя параметры модели и выводя результаты на график. Например, можно:
Показать решение, когда u не зависит от времени, то есть решение в установившемся состоянии. Для этого откройте диалоговое окно Спецификация PDE (PDE Specification) и измените тип PDE на Эллиптический (Elliptic). Полученный раствор в установившемся состоянии находится в тесном согласии с переходным раствором через 20000 секунд.
Показать решение в установившемся состоянии без охлаждения на внешней границе: коэффициент теплопередачи равен нулю. Для этого задайте условие границы Неймана на внешней границе (верхняя сторона прямоугольника) равным g = 0 и q = 0. Полученный график показывает, что температура повышается более чем до 2500 на левом конце стержня.