В этом примере показано, как решить тепловое уравнение, описывающее диффузию тепла в теле. В этом примере используется приложение PDE Modeler. Программный рабочий процесс см. в разделе Теплопередача в блоке с полостью.
Рассмотрим блок, содержащий прямоугольную трещину или полость. Левая сторона блока нагревается до 100 градусов Цельсия. В правой части блока тепло течет от блока к окружающему воздуху с постоянной скоростью, например -10 W/m2. Все остальные границы изолированы. Температура в блоке в начальный момент времени t0 = 0 равна 0 градусам. Цель состоит в моделировании распределения тепла в течение первых пяти секунд.
PDE, регулирующий эту задачу, представляет собой уравнение параболического тепла. Дифференциальное уравнение в частных производных Toolbox™ решает общие параболические PDE вида
au = f
Уравнение тепла имеет вид:
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие действия:
Откройте приложение PDE Modeler с помощью pdeModeler команда.
pdeModeler
Выполните моделирование геометрии: нарисуйте прямоугольник с углами (-0,5, -0,8), (0,5, -0,8), (0,5,0,8) и (-0,5,0,8) и прямоугольник с углами (-0,05, -0,4), (0,05, -0,4), (0,05,0,4) и (-0,05,0,4). Нарисуйте первый прямоугольник с помощью pderect функция.
pderect([-0.5 0.5 -0.8 0.8])
Отображение линий сетки с дополнительными засечками в -0.05 и 0.05. Для этого выберите «Параметры» > «Интервал сетки», снимите флажок «Авто» и введите дополнительные засечки по оси X в -0.05 и 0.05. Затем выберите Опции > Сетка.
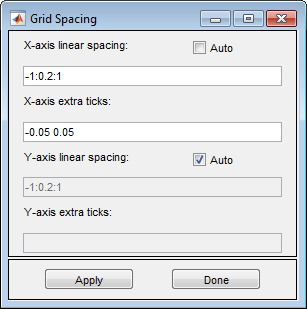
Задайте предел оси X равным [-0.6 0.6] и ограничение оси y до [-1 1]. Для этого выберите Опции (Options) > Границы осей (Axes Limits) и задайте соответствующие диапазоны.
Выберите «Параметры» > «Привязка», чтобы выровнять любую новую форму по линиям сетки. Затем нарисуйте прямоугольник с углами (-0,05, -0,4), (0,05, -0,4), (0,05,0,4) и (-0,05,0,4)
Моделирование геометрии путем ввода R1-R2 в поле Задать формулу.
Убедитесь, что установлен режим приложения Generic Scalar.
Задайте граничные условия. Для этого переключитесь в граничный режим, выбрав «Граница» > «Граничный режим». Затем выберите «Граница» > «Задать граничные условия» и укажите граничное условие Неймана.
Для удобства сначала задайте изолирующее граничное условие Неймана ∂u/∂n = 0 для всех границ. Для этого выделите все границы с помощью команды «Правка» > «Выделить все» и укажите g = 0, q = 0.
Задайте граничное условие Дирихле u = 100 для левой стороны блока. Для этого укажите h = 1, r = 100.
Задайте граничное условие Неймана ∂u/∂n = -10 для правой стороны блока. Для этого укажите g = -10, q = 0.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Уравнение тепла является параболическим уравнением, поэтому выберите параболический тип PDE. Определить c = 1, a = 0, f = 0, и d = 1.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку». Уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».
Установите начальное значение 0, время решения 5 секунд и вычисляйте решение каждые 0,5 секунды. Для этого выберите «Решение» > «Параметры». В диалоговом окне «Параметры решения» задайте время равным 0:0.5:5, и u (t0) в0.
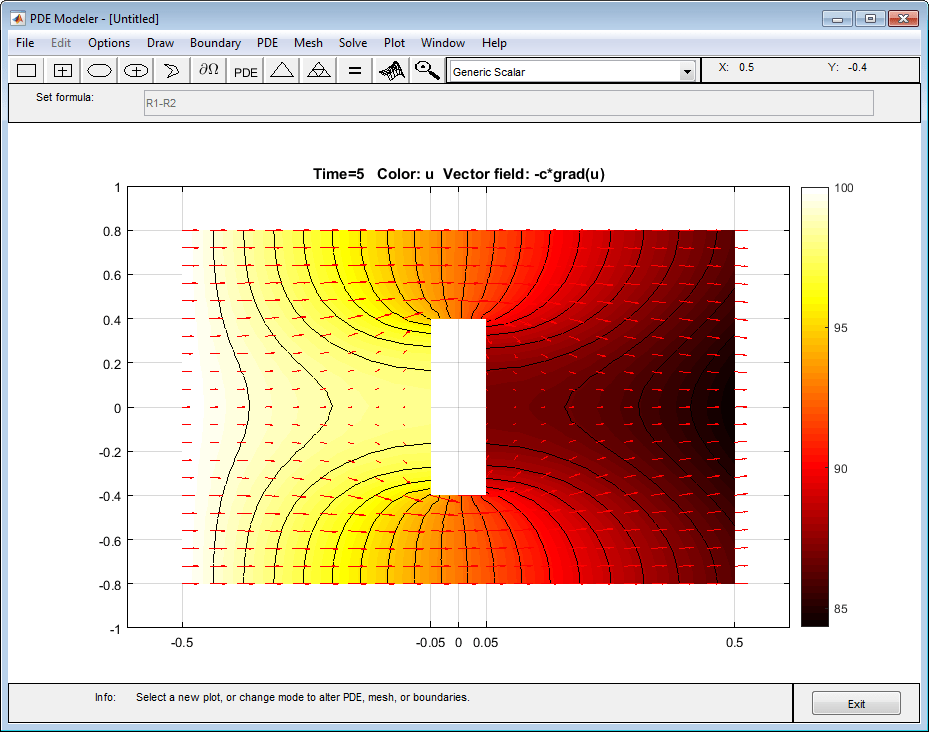
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов. Приложение решает тепловое уравнение в 11 различных моментов времени от 0 до 5 секунд и отображает распределение тепла в конце интервала времени.
Постройте график изотермических линий с использованием контурного графика и поля вектора теплового потока с помощью стрелок и измените карту цветов на hot. Для этого:
Выберите «Печать» > «Параметры».
В открывшемся диалоговом окне выберите параметры «Цвет», «Контур» и «Стрелки». Выбрать -c*grad(u) из раскрывающегося меню «Стрелки».
Измените карту цветов на hot с помощью соответствующего раскрывающегося меню в том же диалоговом окне.
Используйте анимированный график для визуализации динамического поведения температуры. Для этого выберите «Печать» > «Параметры», а затем выберите параметр «Анимация».
Температура в блоке повышается очень быстро. Чтобы улучшить анимацию и сосредоточиться на первой секунде, измените список времени на выражение MATLAB ®logspace(-2,0.5,20). Для этого выберите «Решение» > «Параметры». В диалоговом окне «Параметры решения» задайте время равным logspace(-2,0.5,20).
Можно исследовать решение, изменяя параметры модели и выводя результаты на график. Например, изменить коэффициент теплоемкости d и тепловой поток на правой границе, чтобы увидеть, как эти параметры влияют на распределение тепла.