Решите следующую проблему теплопередачи с различными параметрами материала. В этом примере используется приложение PDE Modeler. Сведения о решениях в командной строке см. в разделе Теплопередача между двумя квадратами, выполненными из различных материалов.
Геометрия 2-D для этой задачи - квадрат со встроенным ромбом (квадрат с поворотом на 45 градусов). PDE, регулирующий эту задачу, представляет собой уравнение параболического тепла:
текст − T)
где start- плотность, C - теплоемкость, k - коэффициент теплопроводности, Q - источник тепла, h - коэффициент конвективной теплопередачи, а Text - внешняя температура.
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие действия:
Моделирование геометрии: нарисуйте квадратную область с углами в (0,0), (3,0), (3,3) и (0,3) и ромбовидную область с углами в (1,5,0,5), (2,5,1,5), (1,5,2,5) и (0,5,1,5).
pderect([0 3 0 3]) pdepoly([1.5 2.5 1.5 0.5],[0.5 1.5 2.5 1.5])
Задайте предел оси X равным [-1.5 4.5] и ограничение оси y до [-0.5 3.5]. Для этого выберите Опции (Options) > Границы осей (Axes Limits) и задайте соответствующие диапазоны.
Установите режим приложения «Теплопередача».
Температура поддерживается на уровне 0 на всех внешних границах, поэтому нет необходимости изменять граничное условие Дирихле по умолчанию T = 0.
Укажите коэффициенты. Для этого выберите PDE > PDE Mode. Затем щелкните каждую область и выберите PDE > PDE Specification или нажмите кнопку PDE на панели инструментов. Поскольку решается уравнение параболического тепла, выберите параболический тип PDE для обеих областей. Для квадратной области задайте следующие коэффициенты:
Плотность, pho = 2
Теплоемкость, C = 0.1
Коэффициент теплопроводности, k = 10
Источник тепла, Q = 0
Коэффициент конвективной теплопередачи, h = 0
Внешняя температура, Text = 0
Для ромбовидной области задайте следующие коэффициенты:
Плотность, pho = 1
Теплоемкость, C = 0.1
Коэффициент теплопроводности, k = 2
Источник тепла, Q = 4
Коэффициент конвективной теплопередачи, h = 0
Внешняя температура, Text = 0
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку». Для более точного решения уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».
Задайте начальное значение и время решения. Для этого выберите «Решение» > «Параметры».
Динамика для этой проблемы очень быстрая - температура достигает устойчивого состояния примерно за 0,1 единицы времени. Чтобы запечатлеть интересную часть динамики, установите время на logspace(-2,-1,10). Это дает 10 логарифмически разнесенных чисел от 0,01 до 0,1. Установите начальное значение температуры u (t0) в0.
Решите уравнение, выбрав команду Решить (Solve) > Решить PDE (Solve PDE) или нажав кнопку = на панели инструментов.
Постройте график решения. По умолчанию приложение отображает распределение температуры в последний раз. Лучший способ визуализации динамического поведения температуры - анимация решения. Для этого выберите «Печать» > «Параметры» и выберите параметры «Анимация» и «Высота» (3-D график) для анимации 3-D графика. Кроме того, можно выбрать параметр «Печать в сетке x-y», чтобы использовать прямоугольную сетку вместо треугольной сетки по умолчанию. Использование прямоугольной сетки вместо треугольной значительно ускоряет процесс анимации.
Также можно построить изотермические линии с помощью контурного графика и поля вектора теплового потока с помощью стрелок.
Выберите «Печать» > «Параметры».
В открывшемся диалоговом окне снимите флажки «Анимация», «Высота» (3-D график) и «Печать в сетке x-y».
Измените карту цветов на hot с помощью соответствующего раскрывающегося меню в том же диалоговом окне.
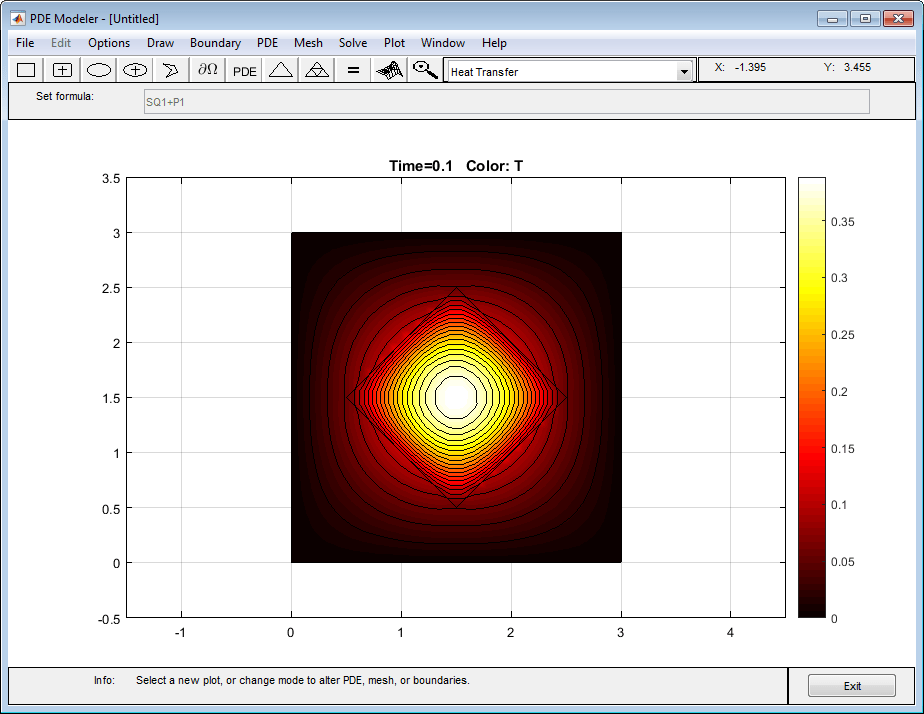
Чтобы получить первый график, выберите параметры «Цвет» и «Контур».
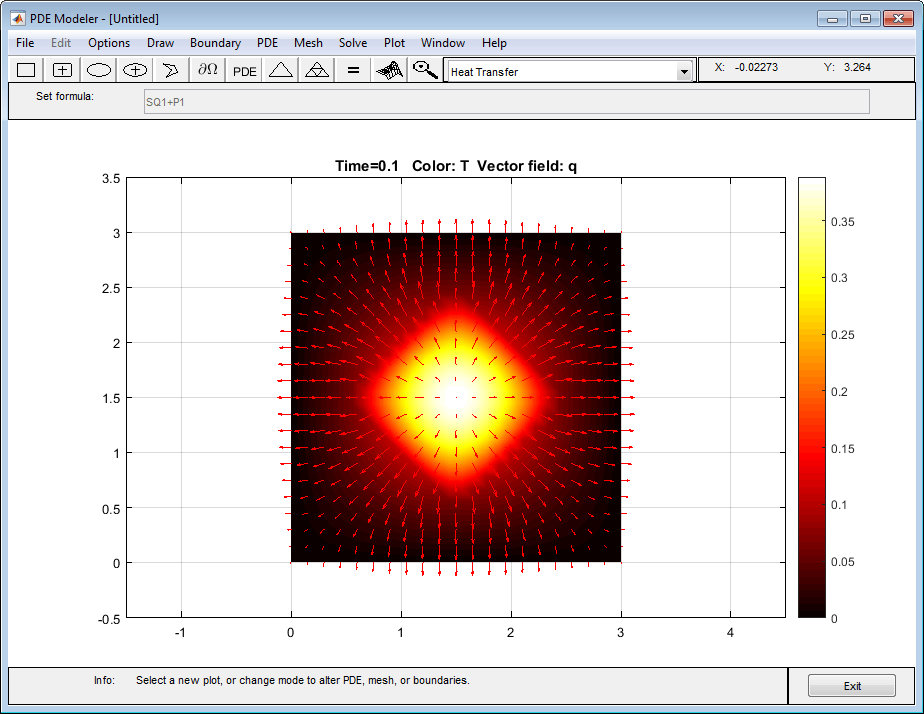
Для второго графика выберите «Цвет» и «Стрелки» и задайте для них значения temperature и heat fluxсоответственно.
Изотермические линии
Температура и тепловой поток