В этом примере показано, как решить простую задачу рассеяния, в которой вычисляются волны, отраженные квадратным объектом, освещенным падающими волнами, идущими слева. В этом примере используется приложение PDE Modeler. Программный рабочий процесс см. в разделе Проблема рассеяния.
Для этой проблемы предположим, что бесконечная горизонтальная мембрана подвергается небольшим вертикальным смещениям U. Мембрана закреплена на границе объекта. Среда однородна, а фазовая скорость (скорость распространения) волны α постоянна. Волновое уравнение
Решение U представляет собой сумму падающей волны V и отраженной волны R:
U = V + R
Когда освещение является гармоническим во времени, можно вычислить поле, решив одну устойчивую задачу. Предположим, что падающая волна является плоской волной, проходящей в направлении -x:
Отраженная волна может быть разложена на пространственные и временные компоненты:
y) e − istartt
Теперь можно переписать волновое уравнение как уравнение Гельмгольца для пространственной составляющей отраженной волны с волновым числом k = λ/α:
-Δr - k2r = 0
Граничное условие Дирихле для границы объекта равно U = 0, или в терминах падающих и отраженных волн R = -V. Для решения временной гармоники и падающей волны, проходящей в направлении -x, можно записать это граничное условие следующим образом:
e − ikx
Отраженная волна R перемещается наружу от объекта. Условие на внешней вычислительной границе должно позволять волнам проходить без отражения. Такие условия обычно называют нерефлексирующими. Когда приближается к бесконечности, R приблизительно удовлетворяет уравнению односторонней волны
В этом уравнении учитываются только волны, движущиеся в положительном направлении. В данном случае, start- радиальное расстояние от объекта. При гармоническом решении по времени это уравнение превращается в обобщённое граничное условие Неймана
Чтобы решить проблему рассеяния в приложении PDE Modeler, выполните следующие действия:
Откройте приложение PDE Modeler с помощью pdeModeler команда.
Задайте предел оси X равным [0.1 1.5] и предел оси y до [0 1]. Для этого выберите Опции (Options) > Границы осей (Axes Limits) и задайте соответствующие диапазоны.
Отображение линий сетки. Для этого:
Выберите «Параметры» > «Интервал сетки» и снимите флажки «Авто».
Введите линейный интервал по оси X как 0.1:0.05:1.5 и линейный интервал по оси Y 0:0.05:1.
Выберите «Параметры» > «Сетка».
Выровняйте новые фигуры по линиям сетки, выбрав «Параметры» > «Привязка».
Нарисуйте квадрат со сторонами длиной 0,1 и центром в [0.8 0.5]. Для этого сначала нажмите
кнопку. Затем щелкните правой кнопкой мыши начало координат и перетащите курсор, чтобы нарисовать квадрат. Щелчок правой кнопкой мыши ограничивает рисованную форму квадратом, а не прямоугольником. Если квадрат не является идеальным, дважды щелкните его. В открывшемся диалоговом окне укажите точное местоположение нижнего левого угла и длину стороны.
Поверните квадрат на 45 градусов. Для этого выберите команду «Рисование» > «Повернуть»... и введите 45 в открывшемся диалоговом окне. Повернутый квадрат представляет освещенный объект.
Нарисуйте окружность с радиусом 0,45 и центром в [0.8 0.5]. Для этого сначала нажмите
кнопку. Затем щелкните правой кнопкой мыши начало координат и перетащите курсор, чтобы нарисовать окружность. Щелчок правой кнопкой мыши ограничивает нарисованную форму так, что она является окружностью, а не эллипсом. Если окружность не является идеальной единицей измерения, дважды щелкните ее. В открывшемся диалоговом окне укажите точное местоположение центра и радиус окружности.
Моделирование геометрии путем ввода C1-SQ1 в поле Задать формулу.
Проверьте, что установлен режим приложения Generic Scalar.
Задайте граничные условия. Для этого переключитесь в граничный режим, выбрав «Граница» > «Граничный режим». Используйте клавиши SHIFT + щелчок для выбора нескольких границ. Затем выберите «Граница» > «Задать граничные условия».
Для периметра окружности граничным условием является граничное условие Неймана с q = -ik, где волновое число k = 60 соответствует длине волны около 0,1 единицы. Войти g = 0 и q = -60*i.
Для периметра квадрата граничным условием является граничное условие Дирихле:
=−eika→ ⋅ x→
В этой задаче, поскольку отраженная волна проходит в направлении -x, граничным условием является r = -e-ikx. Войти h = 1 и r = -exp(-i*60*x).
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Уравнение Гельмгольца - волновое уравнение, но в «Дифференциальном уравнении в частных производных» Toolbox™ его можно рассматривать как эллиптическое уравнение с помощью a = -k2. Определить c = 1, a = -3600, и f = 0.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».
Для достаточной точности необходимо около 10 конечных элементов на длину волны. Внешняя граница должна располагаться на расстоянии нескольких диаметров объекта от самого объекта. Уточните сетку, выбрав меню «Сетка» > «Уточнить сетку». Еще два раза уточните сетку для достижения требуемого разрешения.
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов.
Решение сложное. При построении графика решения появляется предупреждающее сообщение.
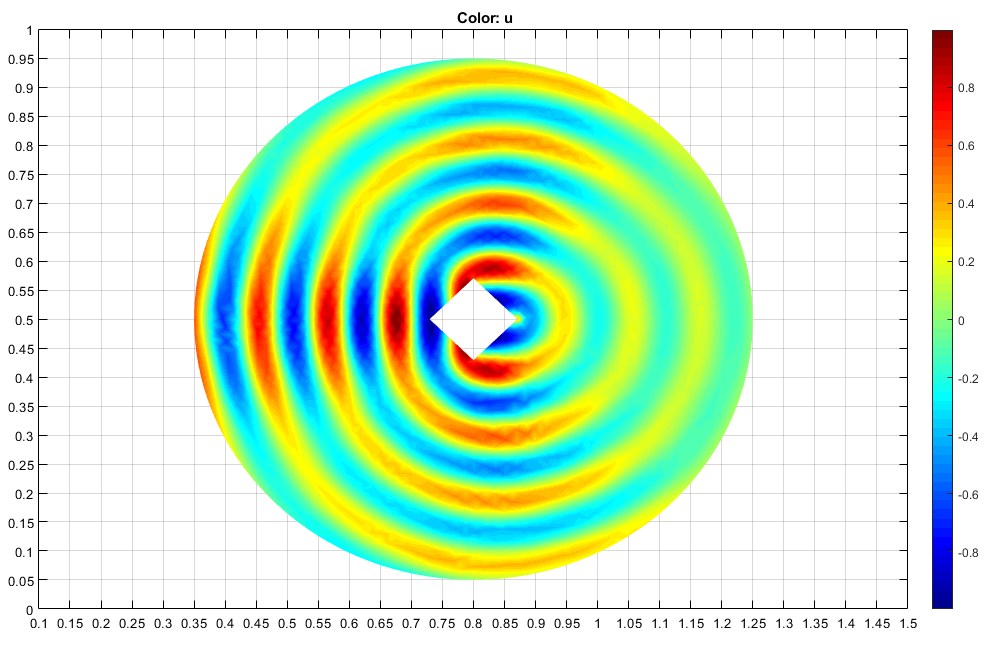
Постройте график отраженных волн. Измените карту цветов на jet выбрав «Печать» > «Параметры», а затем выбрав jet в раскрывающемся меню «Карта цветов».
Анимация решения для зависящего от времени волнового уравнения. Для этого:
Экспортируйте данные сетки и решение в рабочую область MATLAB ®, выбрав меню Сетка (Mesh) > Экспортировать сетку (Export Mesh) и Решение (Solve) > Экспортировать решение (Export Solution) соответственно.
Введите следующие команды в окне команд MATLAB.
figure maxu = max(abs(u)); m = 10; for j = 1:m, uu = real(exp(-j*2*pi/10*sqrt(-1))*u); pdeplot(p,e,t,'XYData',uu,'ColorBar','off','Mesh','off'); colormap(jet) caxis([-maxu maxu]); axis tight ax = gca; ax.DataAspectRatio = [1 1 1]; axis off M(:,j) = getframe; end movie(M);