Чтобы задать параметры для решения PDE, выберите Параметры (Parameters) в меню Решение (Solve). Набор параметров решения зависит от типа PDE. После настройки параметров решите проблему PDE, выбрав пункт Решить PDE (Solve PDE) в меню Решить (Solve) или нажав![]() кнопку.
кнопку.
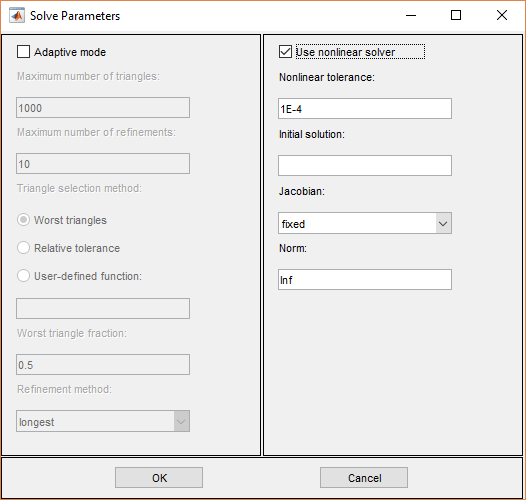
По умолчанию конкретные параметры решения не используются, а эллиптические PDE решаются с помощью базового эллиптического решателя assempde. Дополнительно можно использовать генератор адаптивной сетки и решатель adaptmesh может использоваться. Для адаптивного режима доступны следующие параметры:
Адаптивный режим. Включение/выключение адаптивного режима.
Максимальное количество треугольников. Максимальное допустимое количество новых треугольников (может быть установлено в Inf). Значение по умолчанию рассчитывается на основе текущей сетки.
Максимальное количество уточнений. Максимальное число последовательных уточнений.
Метод выбора треугольника. Существует два метода выбора треугольника, описанных ниже. Также можно предоставить собственную функцию.
Худшие треугольники. Этот метод выбирает все треугольники, которые хуже доли значения наихудшего треугольника (по умолчанию: 0,5).
Относительный допуск. Этот метод выбирает треугольники с использованием критерия относительного допуска (по умолчанию 1E-3).
Определяемая пользователем функция. Введите имя определяемого пользователем метода выбора треугольника. Пример определяемого пользователем метода выбора треугольника см. в разделе Уравнение Пуассона с источником точек и адаптивное уточнение сетки.
Параметр функции. Параметр function позволяет выполнять точную настройку методов выбора треугольника. Для метода наихудшего треугольника (pdeadworst), это доля наихудшего значения, которая используется для определения, какие треугольники нужно уточнить. Для метода относительного допуска это параметр допуска, который управляет тем, насколько хорошо решение подходит для PDE.
Метод уточнения. Может быть regular или longest. См. раздел Определение параметров сетки в приложении PDE Modeler.
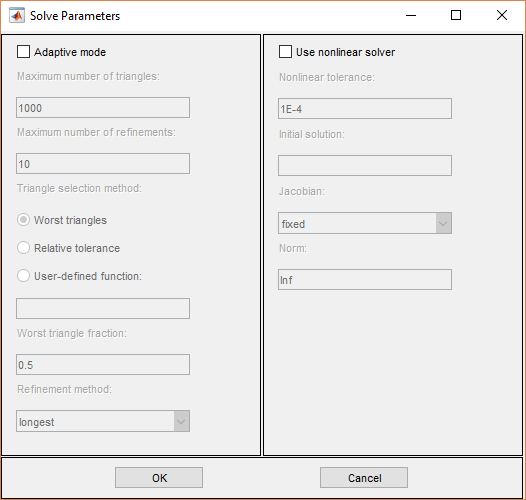
Если проблема нелинейна, то есть параметры в PDE напрямую зависят от решения u, должен использоваться нелинейный решатель. Используются следующие параметры:
Используйте нелинейный решатель. Включение/выключение нелинейного решателя.
Нелинейный допуск. Параметр допуска для нелинейного решателя.
Исходное решение. Первоначальное предположение. Может быть константой или функцией x и y, заданной как выражение MATLAB ®, которое может быть вычислено на узлах текущей сетки .
Примеры: 1, и exp(x.*y). Необязательный параметр, значение по умолчанию равно нулю.
Якобиан. Метод якобианской аппроксимации: fixed (по умолчанию), итерация фиксированной точки, lumped, «комкованное» (диагональное) приближение, или full, полный Якобиан.
Норма. Тип нормы, используемой для вычисления остатка. Введите как energy для энергетической нормы или в качестве реального скалярного p, чтобы дать lp норму. Значение по умолчанию: Inf, бесконечная (максимальная) норма.
Примечание
Адаптивный режим и нелинейный решатель могут использоваться вместе.
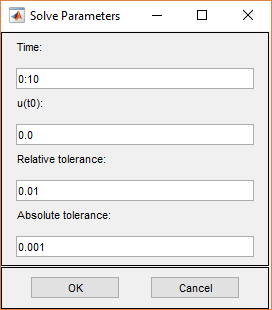
Параметры решения для параболических PDE:
Время. Вектор MATLAB времен, в которые должно быть получено решение параболического PDE. Соответствующий промежуток времени зависит от динамики проблемы.
Примеры: 0:10, и logspace(-2,0,20)
u (t0). Начальное значение u (t0) для параболической задачи PDE Начальное значение может быть константой или вектором столбцов значений на узлах текущей сетки.
Относительный допуск. Параметр относительного допуска для решателя ODE, который используется для решения зависимой от времени части параболической задачи PDE.
Абсолютная толерантность. Параметр абсолютного допуска для решателя ODE, который используется для решения зависимой от времени части параболической задачи PDE.
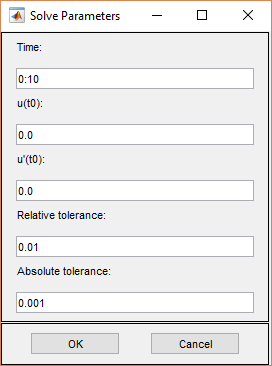
Параметры решения для гиперболических PDE:
Время. Вектор MATLAB времен, в которые должно быть сгенерировано решение гиперболического PDE. Соответствующий промежуток времени зависит от динамики проблемы.
Примеры: 0:10, и logspace(-2,0,20).
u (t0). Начальное значение u (t0) для гиперболической задачи PDE. Начальным значением может быть константа или вектор столбца значений в узлах текущей сетки.
u '(t0). Начальное значение u˙ (t0) для гиперболической задачи PDE. Можно использовать те же форматы, что и для u (t0).
Относительный допуск. Параметр относительного допуска для решателя ODE, который используется для решения зависимой от времени части гиперболической задачи PDE.
Абсолютная толерантность. Параметр абсолютного допуска для решателя ODE, который используется для решения зависимой от времени части гиперболической задачи PDE.
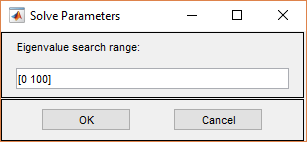
Для PDE собственного значения единственным параметром решения является диапазон поиска собственного значения, двухэлементный вектор, определяющий интервал на вещественной оси как диапазон поиска собственных значений. Левая сторона может быть -Inf.
Примеры: [0 100], [-Inf 50]
Перед решением нелинейного эллиптического PDE в приложении PDE Modeler выберите команду Параметры. Затем выберите Использовать нелинейный решатель (Use nonlinear solver) и нажмите кнопку ОК.