Выберите Режим границы (Boundary Mode) в меню Граница (Boundary) или нажмите
кнопку. Затем выберите границу или несколько границ, для которых задаются условия. Обратите внимание, что если границы не выбраны, то указанные условия применяются ко всем границам.
Чтобы выбрать одну границу, щелкните ее левой кнопкой мыши.
Чтобы выбрать несколько границ и отменить их выбор, используйте клавиши SHIFT + щелчок (или щелкните средней кнопкой мыши).
Чтобы выбрать все границы, используйте опцию «Выбрать все» в меню «Правка».
Выберите пункт Задать граничные условия (Specify Boundary Conditions) в меню Граница (bo
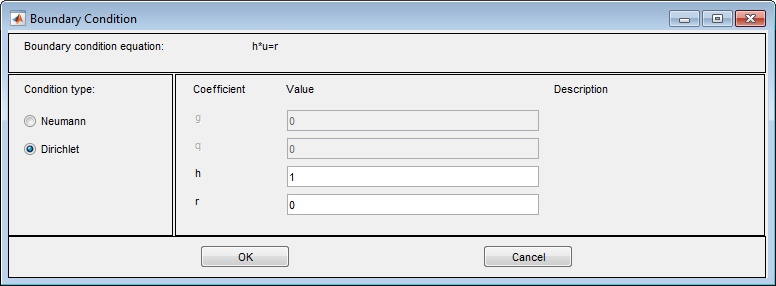
Задать граничные условия (Specify Boundary Conditions) - открытие диалогового окна, в котором можно задать граничные условия для выбранных граничных сегментов. Существует три различных вида условий:
Обобщенные неймановы условия, где граничное условие определяется коэффициентами q и g согласно следующему уравнению:
g.
В системных случаях: q является матрицей 2 на 2 и g является вектором 2 на 1.
Условия Dirichlet: u задается на границе. Уравнение граничного условия hu = r, где h - весовой коэффициент, который может быть применен (обычно 1).
В системных случаях: h является матрицей 2 на 2 и r является вектором 2 на 1.
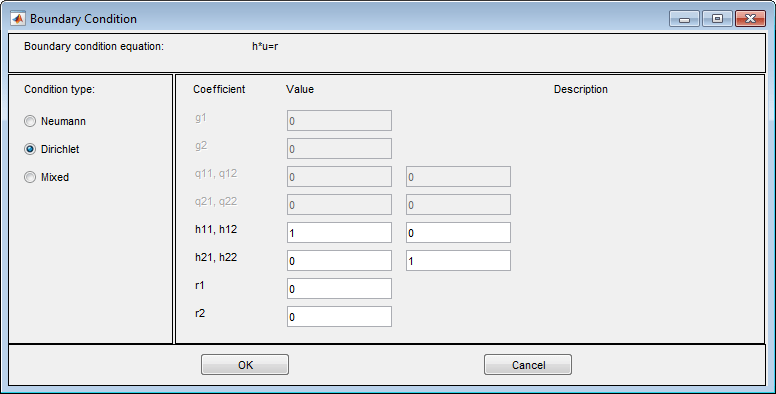
Смешанные граничные условия (только системные случаи), которые представляют собой смесь условий Дирихле и Неймана. q является матрицей 2 на 2, g является вектором 2 на 1, h является вектором 1 на 2, и r является скаляром.
На следующем рисунке показано диалоговое окно для общей системы PDE (Опции > Приложение > Общая система).
Для записей граничного условия можно использовать следующие переменные в допустимом выражении MATLAB ®:
Координаты 2-D x и y.
Параметр граничного сегмента s, пропорционально длине дуги. s равно 0 в начале граничного сегмента и увеличивается до 1 вдоль граничного сегмента в направлении, указанном стрелкой.
Компоненты вектора нормали наружу nx и ny. Если требуется касательный вектор, его можно выразить с помощью nx и ny поскольку tx = -ny и ty = nx.
Решение u.
Время t.
Примечание
Если граничное условие является функцией решения u, необходимо использовать нелинейный решатель. Если граничное условие является функцией времени t, необходимо выбрать параболический или гиперболический PDE.
Примеры: (100-80*s).*nx, и cos(x.^2)
В нестандартных режимах применения столбец Описание (Description) содержит описания физической интерпретации параметров граничных условий.