В этом примере показано, как решить волновое уравнение для поперечных колебаний мембраны на квадрате. Мембрана закреплена с левой и правой сторон и свободна с верхней и нижней сторон. В этом примере используется приложение PDE Modeler. Программный рабочий процесс см. в разделе Уравнение волны в квадратной области.
Волновое уравнение - гиперболический PDE:
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие действия:
Откройте приложение PDE Modeler с помощью pdeModeler команда.
Для отображения линий сетки выберите «Параметры» > «Сетка».
Выровняйте новые фигуры по линиям сетки, выбрав «Параметры» > «Привязка».
Нарисуйте квадрат с углами (-1, -1), (-1,1), (1,1) и (1, -1). Для этого сначала нажмите
кнопку. Затем щелкните один из углов правой кнопкой мыши и перетащите его, чтобы нарисовать квадрат. Щелчок правой кнопкой мыши ограничивает рисованную форму квадратом, а не прямоугольником.
Вы также можете использовать pderect функция:
pderect([-1 1 -1 1])
Убедитесь, что установлен режим приложения Generic Scalar.
Задайте граничные условия. Для этого переключитесь в режим границ, нажав
кнопку или выбрав «Граница» > «Режим границ». Выберите левую и правую границы. Затем выберите «Граница» > «Задать граничные условия» и задайте граничное условие Дирихле u = 0. Это граничное условие по умолчанию (h = 1, r = 0), поэтому вам не нужно менять его.
Для нижней и верхней границ задайте граничное условие Неймана ∂u/∂n = 0. Для этого установите g = 0, q = 0.
Задайте коэффициенты, выбрав спецификацию PDEPDE или нажав кнопку PDE на панели инструментов. Выберите гиперболический тип PDE и укажите c = 1, a = 0, f = 0, и d = 1.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку». Уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».
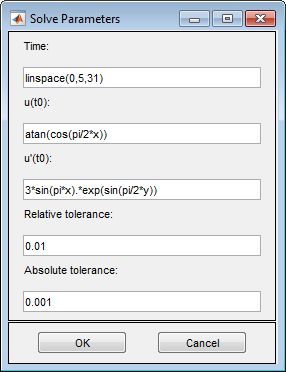
Задайте время решения. Для этого выберите «Решение» > «Параметры». Создание вектора времени с линейным интервалом от 0 до 5 секунд путем установки значения времени решения linspace(0,5,31).
В том же диалоговом окне задайте начальные условия для волнового уравнения. Для хорошо работающего решения начальные значения должны соответствовать граничным условиям. Если начальное время равно t = 0, то следующие начальные значения удовлетворяют граничным условиям: atan(cos(pi/2*x)) для u(0) и 3*sin(pi*x).*exp(sin(pi/2*y)) для ∂u/∂t,
Обратная касательная функция и экспоненциальная функция вводят в решение больше мод.
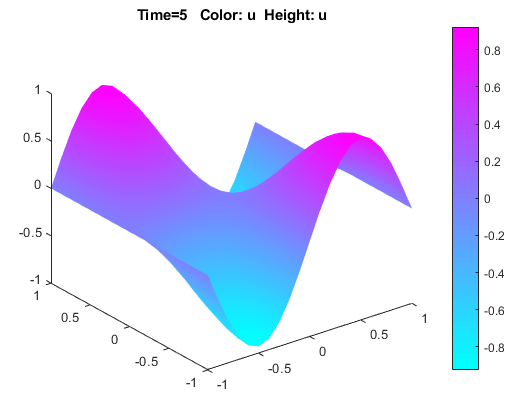
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов. Приложение решает тепловое уравнение в моменты времени от 0 до 5 секунд и отображает результат в конце интервала времени.
Визуализация решения как 3-D статического и анимированного графика. Для этого:
Выберите «Печать» > «Параметры».
В открывшемся диалоговом окне выберите параметры «Цвет и высота» (3-D печать).
Чтобы визуализировать динамическое поведение волны, выберите Анимация (Animation) в том же диалоговом окне. Если анимация выполняется слишком медленно, выберите параметр «Печать в сетке x-y». Сетка x-y может значительно ускорить процесс анимации.
