Exponenta Banner
exponenta event banner

поэтапный. UCA

Однородный круговой массив

развернуть все на странице

Описание

phased.UCA Системный object™ создает однородный циклический массив (UCA). УЦА образован из идентичных сенсорных элементов, равноудаленных по окружности.

Чтобы вычислить отклик для массива для указанных направлений:

  1. Определите и настройте однородный циклический массив. См. раздел Строительство.

  2. Звонить step для вычисления ответа в соответствии со свойствами phased.UCA. Поведение step относится к каждому объекту на панели инструментов.

Примечание

Начиная с R2016b, вместо использования step для выполнения операции, определенной объектом System, можно вызвать объект с аргументами, как если бы это была функция. Например, y = step(obj,x) и y = obj(x) выполнять эквивалентные операции.

Строительство

sUCA = phased.UCA создает объект System с однородным циклическим массивом (UCA), sUCA, состоящий из пяти идентичных изотропных антенных элементов,phased.IsotropicAntennaElement. Элементы равноудалены по окружности радиуса 0,5 метра.

sUCA = phased.UCA(Name,Value) создает объект System, sUCA, с каждым указанным свойством Name, имеющим указанное значение. Можно указать дополнительные аргументы пары имя-значение в любом порядке как (Name1,Value1,...,NameN,ValueN).

sUCA = phased.UCA(N,R) создает системный объект UCA, sUCA, с NumElements свойство имеет значение N и Radius свойство имеет значение R. Этот синтаксис создает УЦА, состоящую из изотропных антенных элементов, phased.IsotropicAntennaElement.

sUCA = phased.UCA(N,R,Name,Value) создает системный объект UCA, sUCA, с NumElements свойство имеет значение N, Radius свойство имеет значение R, и другое указанное свойство Names имеет указанные значения.

Свойства

развернуть все

Элемент матрицы датчика, указанный как антенна или объект System элемента Phased Array System Toolbox. Можно указать антенные элементы, которые поддерживают или не поддерживают поляризацию.

Пример: phased.ShortDipoleAntennaElement()

Число элементов массива, указанное как целое число, большее единицы.

Пример: 3

Радиус массива, заданный как положительный скаляр в метрах.

Пример: 2.5

Нормальное направление массива, указанное как одно из 'x', 'y', или 'z'. Элементы УЦА лежат в плоскости, ортогональной нормальному направлению массива. Векторы визирования элементов лежат в одной плоскости и направлены радиально наружу от начала координат.

Значение свойства ArrayNormalПоложения элементов и направления бурного визирования
'x'Элементы массива лежат на плоскости yz. Все векторы визирования элементов лежат в плоскости yz и указывают наружу от центра массива.
'y'Элементы массива лежат на плоскости zx. Все векторы визирования элементов расположены в плоскости zx и направлены наружу от центра массива.
'z'Элементы массива лежат на плоскости xy. Все векторы визирования элементов лежат в плоскости xy и направлены наружу от центра массива.

Пример: 'y'

Сужение элемента или надбавка, определенная как скаляр со сложным знаком, вектор ряда 1 на Н или вектор колонки N-1. Величина N представляет количество элементов массива. Конусы, также известные как веса, прикладываются к каждому элементу датчика в матрице датчиков и модифицируют как амплитуду, так и фазу принимаемых данных. Если 'Taper' является скаляром, одинаковое значение конусности применяется ко всем элементам. Если 'Taper' является вектором, каждое значение конусности применяется к соответствующему элементу датчика.

Пример: [1 2 3 2 1]

Методы

Специфично для phased.URA Объект
beamwidth

Вычислить и отобразить ширину луча массива

collectPlaneWave

Моделирование принятых плоских волн

directivity

Направленность однородной круговой матрицы

getElementNormal

Нормальные векторы для элементов массива

getElementPosition

Положения элементов массива

getElementSpacing

Интервал между элементами массива

getNumElements

Количество элементов в массиве

getTaper

Элементы массива сужаются

isPolarizationCapable

Поляризационная способность

pattern

Печать массива UCA

patternAzimuth

Постройте график зависимости направленности или шаблона массива UCA от азимута

patternElevation

Печать направленности или массива UCA в зависимости от отметки

step

Выходные отклики элементов массива

viewArray

Просмотр геометрии массива

Общие для всех системных объектов
release

Разрешить изменение значения свойства объекта системы

Примеры

свернуть все

Открыть сценарий в реальном времени

Создайте 11-элементную однородную кольцевую матрицу (UCA), имеющую радиус 1,5 м и работающую на частоте 500 МГц. Решетка состоит из короткодипольных антенных элементов. Сначала отобразите вертикальную составляющую отклика по азимуту 45 градусов и отметке 0 градусов. Затем постройте график направлений по азимуту и отметке.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[50e6,1000e6],...
    'AxisDirection','Z');
array = phased.UCA('NumElements',11,'Radius',1.5,'Element',antenna);
fc = 500e6;
ang = [45;0];
resp = array(fc,ang);
disp(resp.V)
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247
   -1.2247

Отображение диаграммы направленности азимута на частоте 500 МГц для углов азимута от -180 до 180 градусов.

c = physconst('LightSpeed');
pattern(array,fc,[-180:180],0,'Type','directivity','PropagationSpeed',c)

Отображение диаграммы направленности отметок с частотой 500 МГц для углов отметок от -90 до 90 градусов.

pattern(array,fc,[0],[-90:90],'Type','directivity','PropagationSpeed',c)

Алгоритмы

УЦА образован из N идентичных сенсорных элементов, равноудаленных по окружности радиуса R. Окружность лежит в плоскости xy локальной системы координат, начало координат которой лежит в центре окружности. Положения элементов определяются относительно локальной системы координат массива. Круговой массив лежит в плоскости xy системы координат. Нормаль к плоскости УЦА лежит вдоль положительной оси z. Элементы ориентированы таким образом, что их основные направления отклика (нормали) направлены радиально наружу в плоскости xy.

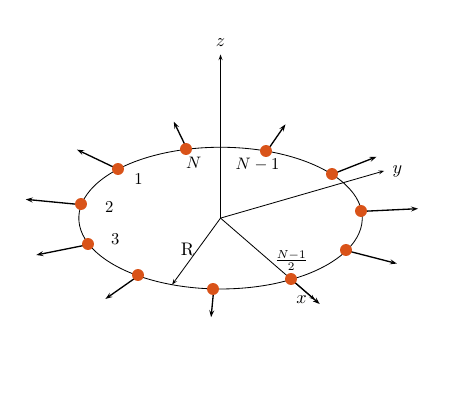
Если число элементов массива нечетное, средний элемент лежит на оси X. Если число элементов является четным, средняя точка между двумя средними элементами лежит на оси X. Для массива из N элементов азимутальный угол положения n-го элемента задается

dwfn = (− (N − 1 )/2 + n  −  1 ) ⋅360/N n = 1,..., N

Азимутальный угол определяется как угол в плоскости xy от оси x к оси y. Угол места определяется как угол от плоскости xy к оси Z. Угловое расстояние между любыми двумя соседними элементами равно 360/N градусам. Значения угла азимута в градусах. Углы возвышения для всех элементов массива равны нулю.

Ссылки

[1] Брукнер, Э., ред. Радиолокационная технология. Лексингтон, Массачусетс: LexBook, 1996.

[2] Деревья фургонов, H. Оптимальная обработка массива. Нью-Йорк: Wiley-Interscience, 2002, стр. 274-304.

Расширенные возможности

.

См. также

| | | | | | | | |

Темы

Представлен в R2015a

Документация по панели инструментов системы поэтапной обработки массивов

Поддержка