Моделирование принятого сигнала в матрице датчиков
x = sensorsig(pos,ns,ang)pos представляет положения элементов массива, каждый из которых предполагается изотропным. ns указывает количество снимков моделируемого сигнала. ang представляет входящие направления каждого сигнала плоской волны. Предполагается, что сигналы плоских волн являются сигналами постоянного модуля со случайными фазами.
Смоделировать принятый сигнал в массиве и использовать данные для оценки направлений поступления.
Примечание.Этот пример выполняется только в R2016b или более поздних версиях. При использовании более ранней версии замените каждый вызов функции эквивалентным step синтаксис. Например, заменить myObject(x) с step(myObject,x).
Создайте 8-элементную однородную линейную матрицу, элементы которой разнесены на половину длины волны.
fc = 3e8; c = 3e8; lambda = c/fc; array = phased.ULA(8,lambda/2);
Смоделировать 100 снимков принятого сигнала в массиве. Предположим, что имеется два сигнала, поступающих от азимута 30 ° и 60 ° соответственно. Шум является белым для всех элементов матрицы, а SNR равен 10 дБ.
x = sensorsig(getElementPosition(array)/lambda,...
100,[30 60],db2pow(-10));Используйте блок оценки пространственного спектра диаграммы направленности для оценки направлений поступления на основе смоделированных данных.
estimator = phased.BeamscanEstimator('SensorArray',array,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = estimator(x);
Постройте график пространственного спектра, полученного в результате процесса оценки.
plotSpectrum(estimator)

На графике показаны пики при 30 ° и 60 °.
Имитация приема двух некоррелированных входящих сигналов с различными уровнями мощности. Вектор с именем scov сохраняет уровни мощности.
Создайте 8-элементную однородную линейную матрицу, элементы которой разнесены на половину длины волны.
fc = 3e8; c = 3e8; lambda = c/fc; ha = phased.ULA(8,lambda/2);
Смоделировать 100 снимков принятого сигнала в массиве. Предположим, что один входящий сигнал исходит от 30 градусов азимута и имеет мощность 3 Вт. Второй входящий сигнал исходит от 60 градусов азимута и имеет мощность 1 Вт. Эти два сигнала не коррелируют друг с другом. Шум является белым для всех элементов матрицы, а SNR равен 10 дБ.
ang = [30 60];
scov = [3 1];
x = sensorsig(getElementPosition(ha)/lambda,...
100,ang,db2pow(-10),scov);Используйте блок оценки пространственного спектра диаграммы направленности для оценки направлений поступления на основе смоделированных данных.
hdoa = phased.BeamscanEstimator('SensorArray',ha,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = step(hdoa,x);
Постройте график пространственного спектра, полученного в результате процесса оценки.
plotSpectrum(hdoa);

График показывает высокий пик при 30 градусах и нижний пик при 60 градусах.
Моделирование приема трех сигналов, два из которых коррелируются.
Создайте матрицу ковариации сигнала, в которой первый и третий из трех сигналов коррелируют друг с другом.
scov = [1 0 0.6;... 0 2 0;... 0.6 0 1];
Смоделировать прием 100 снимков трех входящих сигналов от азимута 30 °, 40 ° и 60 ° соответственно. Матрица, принимающая сигналы, представляет собой 8-элементную однородную линейную матрицу, элементы которой разнесены на половину длины волны. Шум является белым для всех элементов матрицы, а SNR равен 10 дБ.
pos = (0:7)*0.5; ns = 100; ang = [30 40 60]; ncov = db2pow(-10); x = sensorsig(pos,ns,ang,ncov,scov);
Имитация приема сигнала в URA. Сравните теоретическую ковариацию сигнала с ее выборкой ковариации.
Создайте однородную прямоугольную матрицу 2 на 2, имеющую элементы, разнесенные на 1/4 длины волны.
pos = 0.25 * [0 0 0 0; -1 1 -1 1; -1 -1 1 1];
Определите мощность шума независимо для каждого из четырех элементов массива. Каждая запись в ncov - мощность шума элемента матрицы. Эта позиция элемента является соответствующим столбцом в pos. Предположим, что шум не коррелирует между элементами.
ncov = db2pow([-9 -10 -10 -11]);
Смоделировать 100 снимков принятого сигнала в массиве и сохранить теоретическую и эмпирическую ковариационные матрицы. Предположим, что один входящий сигнал исходит от азимута 30 ° и отметки 10 °. Второй входящий сигнал исходит от азимута 50 ° и отметки 0 °. Сигналы имеют мощность 1 Вт и не коррелируются.
ns = 100;
ang1 = [30; 10];
ang2 = [50; 0];
ang = [ang1, ang2];
rng default
[x,rt,r] = sensorsig(pos,ns,ang,ncov);Просмотрите величины теоретической ковариации и ковариации образца.
abs(rt)
ans = 4×4
2.1259 1.8181 1.9261 1.9754
1.8181 2.1000 1.5263 1.9261
1.9261 1.5263 2.1000 1.8181
1.9754 1.9261 1.8181 2.0794
abs(r)
ans = 4×4
2.2107 1.7961 2.0205 1.9813
1.7961 1.9858 1.5163 1.8384
2.0205 1.5163 2.1762 1.8072
1.9813 1.8384 1.8072 2.0000
Имитация приема сигнала в ULA, где шум между различными датчиками коррелирован.
Создайте 4-элементную однородную линейную матрицу, элементы которой разнесены на половину длины волны.
pos = 0.5 * (0:3);
Определите матрицу ковариации шума. Значение в позиции (k,_j_) в ncov матрица - ковариация между k и j элементами массива, перечисленными в массиве.
ncov = 0.1 * [1 0.1 0 0; 0.1 1 0.1 0; 0 0.1 1 0.1; 0 0 0.1 1];
Смоделировать 100 снимков принятого сигнала в массиве. Предположим, что один входящий сигнал исходит от азимута 60 °.
ns = 100; ang = 60; [x,rt,r] = sensorsig(pos,ns,ang,ncov);
Просмотрите теоретическую и выборочную ковариационные матрицы для принятого сигнала.
rt,r
rt = 4×4 complex
1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i -0.3033 - 0.9529i
-0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i
0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i
-0.3033 + 0.9529i 0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i
r = 4×4 complex
1.1059 + 0.0000i -0.8681 - 0.4116i 0.6550 + 0.7017i -0.3151 - 0.9363i
-0.8681 + 0.4116i 1.0037 + 0.0000i -0.8458 - 0.3456i 0.6578 + 0.6750i
0.6550 - 0.7017i -0.8458 + 0.3456i 1.0260 + 0.0000i -0.8775 - 0.3753i
-0.3151 + 0.9363i 0.6578 - 0.6750i -0.8775 + 0.3753i 1.0606 + 0.0000i
pos - Положения элементов в матрице датчиковПозиции элементов в матрице датчиков, определяемые как вектор или матрица N-столбца. Значения в матрице находятся в единицах длины волны сигнала. Например, [0 1 2] описывает три элемента, которые разнесены на одну длину волны сигнала. N - количество элементов в массиве.
Размеры pos:
Для линейного массива вдоль оси y укажите координаты y элементов в векторе 1-by-N.
Для плоского массива в плоскости yz задайте координаты y и z элементов в столбцах матрицы 2-by-N.
Для массива произвольной формы задайте координаты x, y и z элементов в столбцах матрицы 3-by-N.
Типы данных: double
ns - Количество снимков моделируемого сигналаКоличество снимков моделируемого сигнала, указанное как положительный целочисленный скаляр. Функция возвращает это количество выборок на элемент массива.
Типы данных: double
ang - Направления поступающих плоских волновых сигналовНаправления поступающих сигналов плоских волн, определяемые как вектор или матрица М-столбца в градусах. M - количество входящих сигналов.
Размеры ang:
Если ang является матрицей 2-by-M, каждый столбец определяет направление. Каждый столбец находится в форме [azimuth; elevation]. Угол азимута должен быть от -180 до 180 градусов включительно. Угол возвышения должен быть от -90 до 90 градусов включительно.
Если ang является вектором 1-by-M, каждая запись задает азимутальный угол. В этом случае соответствующий угол возвышения принимается равным 0.
Типы данных: double
ncov - Шумовые характеристикиХарактеристики шума, определяемые как неотрицательный скаляр, 1-by-N вектор положительных чисел или N-на-N положительной определенной матрицы.
Размеры ncov:
Если ncov является скаляром, он представляет мощность шума белого шума по всем принимающим чувствительным элементам, в ваттах. В частности, значение 0 указывает на отсутствие шума.
Если ncov является вектором 1-by-N, каждая запись представляет мощность шума одного из сенсорных элементов, в ваттах. Шум не коррелирует между датчиками.
Если ncov является матрицей N-на-N, она представляет собой ковариационную матрицу для шума по всем элементам датчика.
Типы данных: double
scov - Характеристики входного сигналаХарактеристики входящего сигнала, заданные как положительный скаляр, 1-by-M вектор положительных чисел или M-by-M положительная полуопределенная матрица.
Размеры scov:
Если scov - скаляр, он представляет мощность всех входящих сигналов, в ваттах. В этом случае все поступающие сигналы не коррелируются и имеют одинаковый уровень мощности.
Если scov - вектор 1-by-M, каждая запись представляет мощность одного из входящих сигналов, в ваттах. В этом случае все поступающие сигналы не коррелируются друг с другом.
Если scov является матрицей M-by-M, она представляет собой ковариационную матрицу для всех входящих сигналов. Матрица описывает корреляцию между входящими сигналами. В этом случае scov может быть реальным или сложным.
Типы данных: double
taper - Конусность элемента массиваКонусность элемента массива, заданная как скалярный или комплекснозначный вектор N-by-1 столбца. Размерность N - количество элементов массива. Если taper является скаляром, все элементы в массиве используют одно и то же значение. Если taper является вектором, каждая запись определяет конусность, применяемую к соответствующему элементу массива.
Типы данных: double
Поддержка комплексного номера: Да
x - Принятый сигналns-by-N матрицаПринятый сигнал в матрице датчиков, возвращенный как комплексный ns-by-N матрица. Каждый столбец представляет принятый сигнал в соответствующем элементе матрицы. Каждая строка представляет снимок.
rt - Теоретическая ковариационная матрицаТеоретическая ковариационная матрица принятого сигнала, возвращаемая как комплексная матрица N-на-N.
r - Выборка ковариационной матрицыВыборка ковариационной матрицы принятого сигнала, возвращаемая как комплексная матрица N-на-N. N - количество элементов массива. Функция извлекает эту матрицу из x.
Примечание
Если вы указываете этот выходной аргумент, попробуйте сделать ns больше или равно N. В противном случае r является дефицитом ранга.
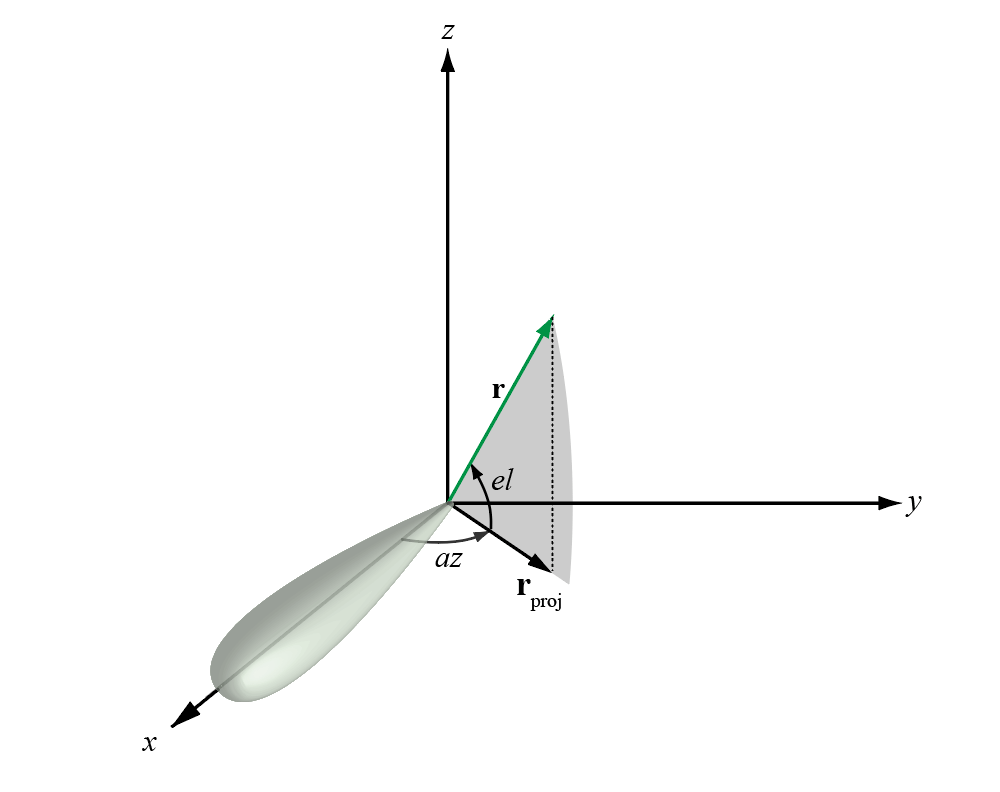
Азимутальный угол вектора - это угол между осью x и ортогональной проекцией вектора на плоскость xy. Угол положителен в направлении от оси x к оси y. Азимутальные углы лежат между -180 и 180 градусами. Угол места - это угол между вектором и его ортогональной проекцией на плоскость xy. При переходе к положительной оси Z от плоскости xy угол является положительным. По умолчанию направление визирования элемента или массива выравнивается по положительной оси X. Направление визирования - это направление главного лепестка элемента или массива.
Примечание
Иногда угол возвышения определяется в литературе как угол вектора с положительной осью z. В продуктах MATLAB ® и Phased Array System Toolbox™ это определение не используется.
Этот рисунок иллюстрирует азимутальный угол и угол возвышения для вектора, показанного зеленой сплошной линией.
Примечания и ограничения по использованию:
Не поддерживает входные данные переменного размера.
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.