Труба (TL)

Закрытый трубопровод для транспортировки жидкости между компонентами термической жидкости

Библиотека:
Simscape/Жидкости/Термическая жидкость/Трубы и фитинги

Описание

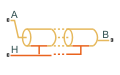
Блок Pipe (TL) моделирует поток термической жидкости через трубу. Температура на трубопроводе рассчитывается по разности температур между портами, отметке трубопровода и любой дополнительной теплопередаче в порту H.

Труба может иметь постоянную или переменную отметку между портами A и B. Для постоянной разности отметок используйте параметр Усиление отметки от порта A к порту B. Можно задать переменную отметку, задав для параметра «Коэффициент усиления отметки» значение Variable. Это открывает физический сигнальный порт EL.

При необходимости можно моделировать динамическую сжимаемость, инерцию и гибкость стенок. При моделировании этих явлений свойства потока вычисляются для каждого заданного количества сегментов трубы.

Гибкость труб

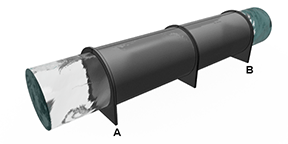
Гибкие стенки моделируются равномерным радиальным расширением, которое сохраняет исходную форму поперечного сечения трубы. Можно задать площадь трубы в параметре «Номинальная площадь поперечного сечения», что означает отсутствие заданной геометрии поперечного сечения, смоделированной блоком. Однако в расчетах теплопередачи и потерь давления блок использует гидравлический диаметр трубы.

Деформация диаметра трубы рассчитывается следующим образом:

$\overset{}{} \frac{_{}}{D˙=DS−Dτ},$

где:

_DS - диаметр трубы после деформации в установившемся состоянии,

$_{DS} =_{} {DN}_{} + {Kc}_{(p} -$ patm),
где Kc - соответствие статического давления диаметру, p - давление в трубке, а _patm - атмосферное давление. Предполагая упругую деформацию тонкостенной трубы с открытым концом, можно вычислить Kc как:

$_{Kc} \frac{=^{}}{}$ D22tE,
где t - толщина стенки трубы, а E - модуль Юнга.
_DN - номинальный диаметр трубы или диаметр, предшествующий деформации:

$_{DN} \sqrt{\frac{=}{}}$ 4Sδ,
где S - номинальная площадь поперечного сечения трубы.
D - гидравлический диаметр трубы.
start- постоянная времени вязкоупругого давления.

Теплопередача у стенки трубы

Теплопередачу к стенам трубы и от них можно моделировать несколькими способами. Существуют две аналитические модели: Gnielinski correlation, который моделирует число Нуссельта как функцию чисел Рейнольдса и Прандтля с предопределенными коэффициентами, и Dittus-Boelter correlation - Nusselt = a*Re^b*Pr^c, который моделирует число Нуссельта как функцию чисел Рейнольдса и Прандтля с пользовательскими коэффициентами.

Nominal temperature differential vs. nominal mass flow rate, Tabulated data - Colburn factor vs. Reynolds number, и Tabulated data - Nusselt number vs. Reynolds number & Prandtl number - это параметры таблицы поиска, основанные на данных, предоставленных пользователем.

Теплопередача между жидкостью и стенкой трубы происходит через конвекцию, QConv и проводимость, QCond.

Теплопередача за счет проводимости составляет:

$_{QCond} \frac{=_{}_{}}{} {kISHD}_{} (_{TH} -$ TI),

где:

D - гидравлический диаметр, если стенки трубы жесткие, и стационарный диаметр трубы, _DS, если стенки трубы гибкие.
_kI - теплопроводность термической жидкости, определяемая внутри для каждого сегмента трубы.
_SH - площадь поверхности стенки трубы.
_TH - температура стенки трубы.
_TI - температура текучей среды, принимаемая во внутреннем узле трубы.

Теплопередача за счет конвекции составляет:

$_{}_{} {\overset{}{}}_{} QConv=cp,Avg'm˙Avg| (_{} TH_{−} TIn) [1 - \frac{_{}}{\exp_{(} {\overset{}{}}_{}}$ −hSHcp,Avg'm˙Avg|)],

где:

cp_{, Avg} - средняя удельная теплота жидкости.
$\overset{}{}$ m˙Avg - средний массовый расход через трубу.
_TIn - температура впускного отверстия для текучей среды.
h - коэффициент теплопередачи трубы.

Коэффициент теплопередачи h составляет:

$h \frac{=_{}}{}$ NukAvgD,

за исключением случаев, когда параметризация выполняется Nominal temperature differential vs. nominal mass flow rateгде _kAvg - средняя теплопроводность термической жидкости по всей трубе, а Nu - среднее число Нуссельта в трубе.

Аналитические параметризации

Если параметризация теплопередачи имеет значение Gnielinski correlation и поток турбулентный, среднее число Нуссельта вычисляется как:

$Nu \frac{\frac{=}{} f8 (Re −}{1000) {Pr1 \frac{+}{}}^{12,7} (^{f8)} 1/2}$ (Pr2/3 − 1),

где:

f - средний коэффициент трения Дарси в соответствии с корреляцией Хааланда:

$f {= {− {1 .}_{} \frac{8log10}{[} 6 {\frac{._{}}{9Re +}}^{(}}^{ϵR3.7D)}$ 1,11]} -2,
где αR - абсолютная шероховатость внутренней поверхности трубы.
Ре - число Рейнольдса.
Pr - число Прандтля.

Когда поток является ламинарным, число Нуссельта является числом Нуссельта для параметра теплопередачи ламинарного потока.

Если параметризация теплопередачи имеет значение Dittus-Boelter correlation и поток турбулентный, среднее число Нуссельта вычисляется как:

$Nu =_{}^{}_{}^{}$ aRebPrc,

где:

a - значение параметра Coefficient a.
b - значение параметра Exponent b.
c - значение параметра Exponent c.

Блок по умолчанию Dittus-Boelter корреляция:

$Nu =_{}^{}_{}^{}$ 0,023Re0.8Pr0.4.

Параметризация по табулированным данным

Если параметризация теплопередачи имеет значение Tabulated data - Colburn factor vs. Reynolds numberсреднее число Нуссельта рассчитывается как:

$Nu =_{} JM ({Re)}_{}^{}$ RePr1/3.

где JM - фактор Колберна-Чилтона.

Если параметризация теплопередачи имеет значение Tabulated data - Nusselt number vs. Reynolds number & Prandtl number, число Нуссельта интерполируется из трехмерного массива среднего числа Нуссельта как функция как среднего числа Рейнольдса, так и среднего числа Прандтля:

$Nu = Nu (Re,$ Pr).

Если параметризация теплопередачи имеет значение Nominal temperature difference vs. nominal mass flow rate и поток турбулентен, коэффициент теплопередачи рассчитывается как:

$\frac{_{}_{}^{}}{{\overset{}{}}_{}^{}} \frac{{\overset{}{}}_{}^{}}{^{h=hNDN1.8m˙N0.8m˙Avg0.8D1.8}},$

где:

$\overset{}{}$ m˙N - номинальный массовый расход.
$\overset{}{}$ m˙Avg - средний массовый расход:

${\overset{}{}}_{} \frac{{\overset{}{}}_{} {\overset{}{}}_{}}{m˙Avg=m˙A+m˙B2} .$
hN - номинальный коэффициент теплопередачи, который рассчитывается как:

$_{} \frac{{\overset{}{}}_{}_{}}{_{}} hN=m˙Ncp,NSH,Nln \frac{(_{TH,} N_{−}}{{TIn}_{,} {NTH}_{, N −}}$ TOut, N),
где:
- _SH, N - номинальная площадь поверхности стенки.
- _TH, N - номинальная температура стенки.
- _TIn, N - номинальная температура притока.
- _TOut, N - номинальная температура оттока.

Это соотношение основано на предположении, что число Нуссельта пропорционально числу Рейнольдса:

$\frac{}{} hDk\propto {\frac{\overset{}{(}}{} m˙DSμ}^{)}$ 0,8.

Если стенки трубы жесткие, выражение коэффициента теплопередачи становится следующим:

$\frac{_{}}{{\overset{}{}}_{}^{}} {\overset{}{}}_{}^{h=hNm˙N0.8m˙Avg0.8} .$

Потери давления из-за вязкого трения

Существует несколько способов моделирования перепада давления по трубе. Haaland correlation предоставляет аналитическую модель для потоков по кольцевым трубам с коэффициентом трения Дарси. Nominal pressure drop vs. nominal mass flow rate и Tabulated data - Darcy friction factor vs. Reynolds number параметризация позволяет предоставлять данные, которые блок будет использовать в качестве справочной таблицы во время моделирования.

Аналитическая параметризация

Если параметризация вязкого трения имеет значение Haaland correlation и поток турбулентный, потеря давления из-за трения на стенках трубы определяется уравнением Дарси-Вайсбаха:

$_{}_{} \frac{{\overset{}{}}_{} {\overset{}{}}_{}}{_{}^{pA−pI=fm˙A'm˙A|2ρIDS2}} \frac{(L_{+}}{}$ LAdd2),

где:

L - длина трубы.
_LE представляет собой совокупную эквивалентную длину локальных сопротивлений, которая представляет собой эквивалентную длину трубки, которая вносит ту же величину потерь, что и сумма потерь, обусловленных другими локальными сопротивлениями в трубке.

Перепад давления между портом B и внутренним узлом I:

$_{}_{} \frac{{\overset{}{}}_{} {\overset{}{}}_{}}{_{}^{pB−pI=fm˙B'm˙B|2ρIDS2}} \frac{(L_{+}}{}$ LAdd2),

Когда поток ламинарный, потери давления из-за трения вычисляются в терминах постоянной трения ламинара для коэффициента трения Дарси, λ. Перепад давления между портом A и внутренним узлом I:

$_{}_{} \frac{{\overset{}{}}_{}}{^{} pA−pI=λμm˙A2ρD2S} \frac{(L_{+}}{}$ LAdd2).

Перепад давления между портом B и внутренним узлом I:

$_{}_{} \frac{{\overset{}{}}_{}}{^{} pB−pI=λμm˙B2ρD2S} \frac{(L_{+}}{}$ LAdd2).

Для переходных потоков перепад давления, обусловленный вязким трением, представляет собой сглаженную смесь между значениями ламинарных и турбулентных потерь давления.

Параметризация по табулированным данным

Если параметризация вязкого трения имеет значение Nominal pressure drop vs. nominal mass flow rate, потери давления из-за вязкого трения рассчитываются по двум половинам трубы с коэффициентом потерь _Kp:

$_{} \frac{}{}_{} {\overset{}{}}_{} \sqrt{{\overset{}{}}_{}^{} {\overset{}{}}_{}^{Δpf,A=12Kpm˙Am˙A2+m˙Th2}}$

$_{} \frac{}{}_{} {\overset{}{}}_{} \sqrt{{\overset{}{}}_{}^{} {\overset{}{}}_{}^{Δpf,B=12Kpm˙Bm˙B2+m˙Th2}}$

где:

${\overset{}{}}_{m˙Th}$ - порог массового расхода для реверсирования потока.
Kp - коэффициент потери давления. Для гибких стенок труб коэффициент потери давления составляет:

$_{} \frac{_{}}{{\overset{}{}}_{}^{}}_{Kp=pNm˙N2DN},$
где:
- _pN - номинальный перепад давления.
- $\overset{}{}$ m˙N - номинальный массовый расход.
Коэффициент потери давления равен

$_{} \frac{_{}}{{\overset{}{}}_{}^{Kp=pNm˙N2}},$
когда стенки трубы являются жесткими. Когда параметры Номинальный перепад давления и Номинальный массовый расход являются векторами, значение _Kp определяется как наименьшая квадратичная посадка векторных элементов.

Когда

Если параметризация вязкого трения имеет значение Tabulated data – Darcy friction factor vs. Reynolds numberкоэффициент трения интерполируется из табулированных данных как функция числа Рейнольдса:

$f = f ($ Re).

Баланс импульса

Перепад давления на трубе обусловлен давлением в отверстиях трубы, трением на стенках трубы и гидростатическими изменениями из-за любого изменения отметки:

$_{pA} -_{} pB_{=}_{} Δpf +$ αIgΔz,

где:

_рА - давление в порту А.
_pB - давление в порту B.
_Δpf - разность давлений, обусловленная вязким трением, _Δpf, A + _Δpf, B.
g - гравитационное ускорение.
Δz - разность высот между портом A и портом B, или _zA - _zB.
_{δ I} - внутренняя плотность текучей среды, измеряемая в каждом сегменте трубы. Если динамическая сжимаемость жидкости не смоделирована, это:

$_{pI} \frac{=_{} {pA}_{}}{+}$ pB2.

Когда инерция жидкости не моделируется, баланс импульса между портом A и внутренним узлом I составляет:

$_{pA} -_{} pI_{=} {Δpf}_{,} \frac{A}{+}$ αIgΔz2.

Когда инерция жидкости не моделируется, баланс импульса между портом B и внутренним узлом I составляет:

$_{pB} -_{} pI_{=} {Δpf}_{,} \frac{B}{−}$ αIgΔz2.

При моделировании инерции жидкости баланс импульса между портом A и внутренним узлом I составляет:

$_{pA} -_{} pI_{=} {Δpf}_{,} \frac{A}{+} \frac{{\overset{}{}}_{}}{} \frac{}{ρIgΔz2}$ + m ASL2,

где:

$\overset{}{}$ _p m A - инерция жидкости в порту A.
L - длина трубы.
S - номинальная площадь поперечного сечения.

При моделировании инерции жидкости баланс импульса между портом B и внутренним узлом I составляет:

$_{pB} -_{} pI_{=} {Δpf}_{,} \frac{B}{−} \frac{{\overset{}{}}_{}}{} \frac{}{ρIgΔz2}$ + m BSL2,

где

$\overset{}{}$ _m B - инерция жидкости в порту B.

Дискретизация труб

Трубу можно разделить на несколько сегментов. Если труба имеет более одного сегмента, для каждого сегмента вычисляются уравнения массового расхода, расхода энергии и баланса импульса. Наличие нескольких сегментов труб позволяет отслеживать изменения переменных, таких как плотность текучей среды, при моделировании динамической сжимаемости текучей среды.

Если вы хотите зафиксировать определенные явления в вашем приложении, такие как водяной молоток, выберите ряд сегментов, которые обеспечивают достаточное разрешение переходного процесса. Следующая формула, из теоремы о выборке Найквиста, предоставляет правило большого пальца для дискретизации трубы на минимум N сегментов:

$N = \frac{}{}$ 2Lfc,

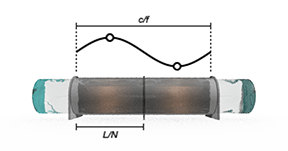
где:

L - длина трубы.
f - переходная частота.
c - скорость звука.

В некоторых случаях, например, при моделировании тепловых переходных процессов вдоль трубы, приложение может быть лучше подходит для последовательного соединения нескольких блоков труб (TL).

Массовый баланс

Для жесткой трубы с несжимаемой жидкостью уравнение обсуждения массы трубы:

${\overset{}{}}_{} {\overset{}{}}_{} m˙A+m˙B=0,$

где:

$\overset{}{}$ m˙A - массовый расход в порту A.
$\overset{}{}$ m˙B - массовый расход в порту B.

Для гибкой трубы с несжимаемой жидкостью уравнение сохранения массы трубы:

${\overset{}{}}_{} {\overset{}{}}_{}_{} \overset{m˙A+m˙B=ρIV˙}{},$

где:

_{δ I} - плотность термической жидкости во внутреннем узле I. Каждый сегмент трубы имеет внутренний узел.
$\overset{V˙}{}$ - скорость деформации объема трубы.

Для гибкой трубы с сжимаемой жидкостью уравнение сохранения массы трубы: Эта зависимость фиксируется модулем объема и коэффициентом теплового расширения термической жидкости:

${\overset{}{}}_{} {\overset{}{}}_{}_{} \overset{}{}_{} m˙A+m˙B=ρIV˙+ρIV \frac{{\overset{}{(}}_{}}{_{}}_{} {\overset{}{}}_{} p˙IβI-αIT˙I$ ),

где:

_pI - тепловое давление жидкости во внутреннем узле I.
$\overset{}{}$ T˙I - скорость изменения температуры термической жидкости во внутреннем узле I.
_βI - модуль объема термической жидкости.
α - коэффициент теплового расширения жидкости.

Энергетический баланс

Скорость накопления энергии в трубе во внутреннем узле I определяется как:

$\overset{}{}_{}_{}_{} {\overset{}{}}_{} E.=ϕA+ϕB+ϕH−m˙AvggΔz,$

где:

_ϕA энергетическая скорость потока жидкости в порту A.
_ϕB энергетическая скорость потока жидкости в порту B.
_ϕH энергетическая скорость потока жидкости в порту H.

Общая энергия определяется как:

$E =_{}_{}$ αIuIV,

где:

_uI - удельная внутренняя энергия текучей среды в узле I.
V - объем трубы.

Если текучая среда является сжимаемой, выражение скорости накопления энергии будет следующим:

$\overset{}{}_{} E˙=ρIV {\frac{(}{} \frac{}{} dudpdpdt \frac{+}{} \frac{}{}}_{} dudTdTdt$ ) I.

Если текучая среда является сжимаемой и стенки трубы являются гибкими, выражение для скорости накопления энергии будет следующим:

$\overset{}{}_{} E˙=ρIV {\frac{(}{} \frac{}{} dudpdpdt \frac{+}{} \frac{}{}}_{} dudTdTdt)_{I}_{+} (_{} {\frac{αIuI}{+}}_{pI})$ (dVdt) I.

Порты

Вход

развернуть все

`EL` - Перепад отметок портов
физический сигнал

Переменная разность отметок между портами A и B, заданная как физический сигнал.

Сохранение

развернуть все

`A` - Открытие трубы
термическая жидкость

Входное или выходное отверстие для жидкости в трубу.

`B` - Открытие трубы
термическая жидкость

Входное или выходное отверстие для жидкости в трубу.

`H` - Трубная стена
тепловой

Температура стенки трубы.

Параметры

развернуть все

Конфигурация

`Fluid dynamic compressibility` - Следует ли моделировать динамическую сжимаемость жидкости
`On` (по умолчанию) | `Off`

Следует ли моделировать какое-либо изменение плотности жидкости из-за сжимаемости жидкости. Если для параметра «Сжимаемость жидкости» установлено значение On, изменения, обусловленные массовым расходом в блок, вычисляются в дополнение к изменениям плотности, обусловленным изменениями давления.

`Fluid inertia` - Следует ли моделировать ускорение жидкости
`On` (по умолчанию) | `Off`

Учитывать ли ускорение в массовом расходе из-за массы жидкости.

Зависимости

Чтобы включить этот параметр, задайте для параметра Динамическая сжимаемость жидкости значение On.

`Number of segments` - Дискретизация труб
`1` (по умолчанию) | положительный безразмерный скаляр

Количество секций труб. Каждое деление представляет собой отдельный сегмент, по которому рассчитывается давление, в зависимости от давления на входе в трубу, сжимаемости жидкости и гибкости стенок, если применимо. Объем жидкости в каждом сегменте остается фиксированным.

Зависимости

Чтобы включить этот параметр, задайте для параметра Динамическая сжимаемость жидкости значение On.

`Pipe total length` - Общая длина трубы
`5 m` (по умолчанию) | положительный скаляр в единицах длины

Общая длина трубы по всем сегментам трубы.

`Nominal cross-sectional area` - Площадь поперечного сечения трубы без деформации
`0.01` m ^ 2 (по умолчанию) | положительный скаляр в единицах площади

Площадь поперечного сечения трубы без деформаций.

`Pipe wall specification` - Определяет гибкость стен
`Rigid` (по умолчанию) | `Flexible`

Определение стенок труб в качестве жестких или гибких. Гибкие стенки моделируются равномерным радиальным расширением, которое сохраняет исходную форму поперечного сечения трубы.

Зависимости

Чтобы включить этот параметр, задайте для параметра Динамическая сжимаемость жидкости значение On.

`Hydraulic diameter` - Эффективный диаметр некруглых труб
`0.1128 m` (по умолчанию) | положительный скаляр в единицах длины

Эффективный диаметр, используемый в уравнениях теплопередачи, баланса импульса и гибкости труб. Для некруглых труб гидравлический диаметр представляет собой эффективный диаметр жидкости в трубе. Для круглых труб гидравлический диаметр и диаметр трубы одинаковы.

Зависимости

Чтобы включить этот параметр, установите один из следующих параметров:

Динамическая сжимаемость жидкости до Off.
Спецификация стенки трубы для Rigid Динамическая сжимаемость жидкости до On.

`Elevation gain specification` - Задать свойство отметки трубы
`Constant` (по умолчанию) | `Variable`

Установить отметку трубы как Constant или Variable. Выбор Variable открывает физический сигнальный порт EL.

`Elevation gain from port A to port B` - Изменение высоты с порта A на порт B
`0 m` (по умолчанию) | положительный скаляр в единицах длины

Перепад отметок для труб с постоянной отметкой. Коэффициент усиления отметки должен быть меньше или равен общей длине трубы.

Зависимости

Чтобы включить этот параметр, задайте для параметра «Коэффициент усиления отметки» значение Constant.

`Gravitational acceleration` - Ускорение от силы тяжести на средней отметке трубы
`9.81 m/s^2` (по умолчанию) | положительный скаляр в единицах длины/времени ^

Постоянная гравитационного ускорения (g) на средней отметке трубы.

`Static pressure-diameter compliance` - Измерение деформации трубы
`1.2e-6 m/MPa` (по умолчанию) | положительный скаляр в единицах длины/давления

Коэффициент радиальной деформации трубы из-за изменения давления. Это свойство материала трубы.

Зависимости

Чтобы включить этот параметр, задайте для параметра «Спецификация стенки трубы» значение Flexible.

`Viscoelastic process time constant` - Постоянная времени деформации трубы
`0.01 s` (по умолчанию) | положительный скаляр в единицах времени

Время, необходимое для достижения стеной стационарного состояния после деформации трубы. Этот параметр влияет на динамическое изменение объема трубы.

Зависимости

Чтобы включить этот параметр, задайте для параметра «Спецификация стенки трубы» значение Flexible.

Вязкое трение

`Viscous friction parameterization` - Модель трения
`Haaland correlation` (по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

Параметризация потерь давления из-за трения стенок. Доступны как аналитические, так и табличные составы.

`Aggregate equivalent length of local resistances` - Незначительные потери давления в трубе, выраженные в виде длины
`1 m` (по умолчанию) | положительный скаляр в единицах длины

Длина трубы, которая приведет к эквивалентным гидравлическим потерям, как труба с изгибами, изменениями площади или другими неоднородностями. Эффективная длина трубы - это сумма длины трубы и эквивалентной длины агрегата локальных сопротивлений.

Зависимости

Чтобы включить этот параметр, установите параметризацию вязкого трения в значение Haaland correlation.

`Internal surface absolute roughness` - Абсолютная шероховатость стенки трубы
`1.5e-5 m` (по умолчанию) | положительный скаляр в единицах длины

Абсолютная шероховатость стенки трубы. Этот параметр используется для определения коэффициента трения Дарси, который способствует потере давления в трубе.

Зависимости

Чтобы включить этот параметр, установите параметризацию вязкого трения в значение Haaland correlation.

`Shape factor for laminar flow viscous friction` - Постоянная трения для ламинарных потоков
`64` (по умолчанию) | положительный безразмерный скаляр

Постоянная трения для ламинарных потоков. Коэффициент трения Дарси отражает вклад трения стенок в расчеты потерь давления.

`Laminar flow upper Reynolds number limit` - число Рейнольдса, ниже которого поток ламинарен
`2e+3` (по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, ниже которого поток ламинарный. Выше этого порога поток переходит в турбулентный, достигая турбулентного режима при установке нижнего предела числа Рейнольдса.

`Turbulent flow lower Reynolds number limit` - число Рейнольдса, выше которого поток турбулентен
`4e+3` (по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, выше которого поток турбулентен. Ниже этого порога поток постепенно переходит в ламинарный режим, достигая ламинарного режима при установке верхнего предела числа Рейнольдса.

`Nominal mass flow rate` - Массовый расход труб
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Номинальный массовый расход трубы, используемый для вычисления коэффициента потери давления, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный перепад давления. Когда этот параметр подается как вектор, скалярное значение Kp определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите параметризацию вязкого трения в значение Nominal pressure drop vs. nominal mass flow rate.

`Nominal pressure drop` - Перепад давления над трубой
`[0.001 0.01] MPa` (по умолчанию) | скаляр или вектор чисел в единицах давления

Номинальный перепад давления в трубе, используемый для вычисления коэффициента потери давления, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход. Когда этот параметр подается как вектор, скалярное значение Kp определяется как аппроксимация векторных элементов методом наименьших квадратов.

Зависимости

`Mass flow rate threshold for flow reversal` - Порог, ниже которого применяется численное сглаживание
`1e-6 kg/s` (по умолчанию) | положительный скаляр в единицах массы/времени

Порог массового расхода для обратного потока. Переходная область определяется около 0 кг/с между положительными и отрицательными значениями порога массового расхода. В этой переходной области к отклику потока применяется численное сглаживание. Пороговое значение должно быть больше 0.

Зависимости

`Reynolds number vector for turbulent Darcy friction factor` - числа Рейнольдса, при которых следует составить таблицу коэффициента трения Дарси
`[ 400 1000 1.5e+3 3e+3 4e+3 6e+3 1e+4 2e+4 4e+4 6e+4 1e+5 1e+8 ]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор чисел Рейнольдса для табличной параметризации коэффициента трения Дарси. Векторные элементы образуют независимую ось с параметром вектора коэффициента трения Дарси. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Для реверсированных потоков, или потоков от B к A, одни и те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите параметризацию вязкого трения в значение Tabulated data - Darcy friction factor vs. Reynolds number.

`Darcy friction factor vector` - Коэффициенты трения Дарси в табличных числах Рейнольдса
`[ 0.264 0.112 0.07099999999999999 0.0417 0.0387 0.0268 0.025 0.0232 0.0226 0.022 0.0214 0.0214 ]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор коэффициентов трения Дарси для табличной параметризации коэффициента трения Дарси. Векторные элементы должны соответствовать одному к одному с элементами в числовом векторе Рейнольдса для турбулентного параметра коэффициента трения Дарси и должны быть уникальны и больше или равны 0.

Зависимости

Теплопередача

`Heat transfer parameterization` - Метод захвата конвективной теплопередачи стенкой трубы
`Gnielinski correlationNominal temperature differential vs. nominal mass flow rate` (по умолчанию) | `Dittus-Boelter correlation` | `Tabulated data - Colburn factor vs. Reynolds number` | `Tabulated data - Nusselt number vs. Reynolds number & Prandtl number`

СПОСОБ РАСЧЕТА КОЭФФИЦИЕНТА ТЕПЛОПЕРЕДАЧИ МЕЖДУ ЖИДКОСТЬЮ И СТЕНКОЙ ТРУБЫ. Доступны аналитические и табличные параметризации данных.

`Nusselt number for laminar flow heat transfer` - Номер Nusselt для использования в расчетах теплопередачи ламинарных потоков
`3.66` (по умолчанию)

Соотношение конвективной и проводящей теплопередачи в ламинарном режиме потока. Количество Нусельта в жидкости влияет на скорость теплопередачи.

Зависимости

Чтобы включить этот параметр, задайте для параметра Теплопередача значение:

Gnielinski correlation.
Nominal temperature differential vs. nominal mass flow rate.
Dittus-Boelter correlation.

`Nominal mass flow rate` - Массовый расход труб
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Номинальный массовый расход трубы, используемый для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальная температура притока. Когда этот параметр подается как вектор, скалярное значение hp определяется как подгонка векторных элементов по методу наименьших квадратов.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow temperature` - Температура на входе в трубопровод
`[293.15 293.15] K` (по умолчанию) | скаляр или вектор чисел в единицах температуры

Номинальная температура на входе жидкости, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход. Когда этот параметр подается как вектор, скалярное значение h определяется как подгонка векторных элементов по методу наименьших квадратов.

Зависимости

`Nominal outflow temperature` - Температура на выходе из трубы
`[300 300] K`'(по умолчанию) | скаляр или вектор чисел в единицах температуры

Номинальная температура на выходе жидкости, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход. Когда этот параметр подается как вектор, скалярное значение h определяется как подгонка векторных элементов по методу наименьших квадратов.

Зависимости

`Nominal inflow pressure` - Давление на входе в трубопровод
`[0.101325 0.101325] MPa` (по умолчанию) | скаляр или вектор чисел в единицах давления

Номинальное давление на входе жидкости, используемое для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход. Когда этот параметр подается как вектор, скалярное значение h определяется как подгонка векторных элементов по методу наименьших квадратов.

Зависимости

`Nominal wall temperature` - Температура стенки трубы
`[303.15 303.15] K` (по умолчанию) | скаляр или вектор чисел в единицах температуры

Температура стенки трубы, используемая для вычисления коэффициента теплопередачи, заданного как скаляр или вектор. Все номинальные значения должны быть больше 0 и иметь то же количество элементов, что и параметр Номинальный массовый расход. Когда этот параметр подается как вектор, скалярное значение h определяется как подгонка векторных элементов по методу наименьших квадратов.

Зависимости

Чтобы включить эту температуру, установите параметризацию теплопередачи в значение Nominal temperature differential vs. nominal mass flow rate.

`Coefficient a` - Эмпирическая константа a корреляции Диттуса-Болтера
`0.023` (по умолчанию) | положительный безразмерный скаляр

Эмпирическая константа a для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Dittus-Boelter correlation.

`Exponent b` - Эмпирическая константа b корреляции Диттуса-Болтера
`0.8` (по умолчанию) | положительный безразмерный скаляр

Эмпирическая константа b для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Dittus-Boelter correlation.

`Exponent c` - Эмпирическая константа c корреляции Диттуса-Болтера
`0.4` (по умолчанию) | положительный безразмерный скаляр

Эмпирическая константа c для использования в корреляции Диттуса-Болтера. Корреляция связывает число Нуссельта в турбулентных потоках с коэффициентом теплопередачи. Значение по умолчанию отражает теплопередачу жидкости.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Dittus-Boelter correlation.

`Reynolds number vector for Colburn factor` - числа Рейнольдса, для которых следует составить таблицу коэффициента Колберна
`[100 150 1000]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор чисел Рейнольдса для табличной параметризации фактора Колберна. Векторные элементы образуют независимую ось с параметром вектора фактора Колберна. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Этот параметр должен иметь то же количество элементов, что и вектор фактора Колберна. Для реверсированных потоков, или потоков от B к A, одни и те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Tabulated data - Colburn factor vs. Reynolds number.

`Colburn factor vector` - Факторы Колберна, при которых табличные числа Рейнольдса
`[0.019 0.013 0.002]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор факторов Колбруна для табличной параметризации фактора Колберна. Векторные элементы образуют независимую ось с числовым вектором Рейнольдса для параметра фактора Колберна. Этот параметр должен иметь то же количество элементов, что и вектор числа Рейнольдса для фактора Колберна.

Зависимости

Этот параметр активен, если для параметра блока параметризации теплопередачи задано значение Tabulated data - Colburn factor vs. Reynolds number.

`Reynolds number vector for Nusselt number` - число Рейнольдса, для которого необходимо составить таблицу числа Нуссельта
`[100 150 100]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор чисел Рейнольдса для табличной параметризации числа Нуссельта. Этот вектор образует независимую ось с числовым вектором Прандтля для параметра числа Нуссельта для зависимой от 2-D таблицы чисел Нуссельта. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0.

Зависимости

Чтобы включить этот параметр, установите параметризацию теплопередачи в значение Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Prandtl number vector for Nusselt number` - Числа Прандтля, для которых необходимо составить таблицу номера Нуссельта
`[1 10]` (по умолчанию) | вектор положительных безразмерных чисел

Вектор чисел Прандтля для табличной параметризации числа Нуссельта. Этот вектор образует независимую ось с числовым вектором Рейнольдса для параметра числа Нуссельта для зависимой от 2-D таблицы чисел Нуссельта. Векторные элементы должны быть перечислены в порядке возрастания.

Зависимости

`Nusselt number table` - Числа Нуссельта в табличных числах Рейнольдса и Прандтля
`[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ]` (по умолчанию) | матрица положительных безразмерных чисел

Матрица M-by-N чисел Нуссельта в указанных числах Рейнольдса и Прандтля. Между элементами таблицы используется линейная интерполяция. M и N - размеры соответствующих векторов:

M - число векторных элементов в числовом векторе Рейнольдса для числового параметра Нуссельта.
N - число векторных элементов в числовом векторе Прандтля для числового параметра Нуссельта.

Зависимости

Начальные условия

`Initial liquid temperature` - Абсолютная температура в трубе в начале моделирования
`293.15 K` (по умолчанию) | положительный скаляр или вектор в единицах измерения температуры

Температура жидкости в начале моделирования, заданная как скаляр или вектор. Вектор n элементов в длину определяет температуру жидкости для каждого из n сегментов трубы. Если вектор имеет длину двух элементов, температура вдоль трубы линейно распределяется между двумя значениями элементов. Если вектор имеет длину три или более элементов, начальная температура в n-м сегменте задается n-м элементом вектора.

`Initial liquid pressure` - Абсолютное давление в трубе в начале моделирования
`0.101325 MPa` (по умолчанию) | положительный скаляр или вектор в единицах давления

Абсолютное давление жидкости в начале моделирования, определяемое как скаляр или вектор. Вектор n элементов в длину определяет давление жидкости для каждого из n сегментов трубы. Если вектор имеет длину в два элемента, давление вдоль трубы линейно распределяется между двумя значениями элементов. Если вектор имеет длину три или более элементов, начальное давление в n-м сегменте задается n-м элементом вектора.

Примеры модели

Система отопления дома

Смоделировать простую систему отопления дома. Модель содержит нагреватель, контроллер и конструкцию дома с четырьмя радиаторами и четырьмя комнатами. Каждая комната обменивается теплом с окружающей средой через внешние стены, крышу и окна. Каждый путь моделируется как комбинация тепловой конвекции, тепловой проводимости и тепловой массы. Предполагается, что тепло не передается внутри помещений. Нагреватель состоит из печи, котла, аккумулятора и насоса для циркуляции горячей воды в системе. Контроллер начинает прием топлива в печь, если общая средняя температура помещений падает ниже 21 градуса C, и останавливается, если температура превышает 25 градусов C. Моделирование рассчитывает стоимость отопления и температуру внутри помещения.

Управление теплом электромобилей

Моделирует систему терморегуляции электромобиля аккумуляторной батареи. Система состоит из двух контуров охлаждающей жидкости, контура охлаждения и контура ОВКВ кабины. Тепловой нагрузкой являются батареи, силовой агрегат и кабина.

Документация

Труба (TL)

Описание

Гибкость труб

Теплопередача у стенки трубы

Потери давления из-за вязкого трения

Баланс импульса

Дискретизация труб

Массовый баланс

Энергетический баланс

Порты

Вход

EL - Перепад отметок портов физический сигнал

Сохранение

A - Открытие трубы термическая жидкость

B - Открытие трубы термическая жидкость

H - Трубная стена тепловой

Параметры

Fluid dynamic compressibility - Следует ли моделировать динамическую сжимаемость жидкости On (по умолчанию) | Off

Fluid inertia - Следует ли моделировать ускорение жидкости On (по умолчанию) | Off

Зависимости

Number of segments - Дискретизация труб 1 (по умолчанию) | положительный безразмерный скаляр

Зависимости

Pipe total length - Общая длина трубы 5 m (по умолчанию) | положительный скаляр в единицах длины

Nominal cross-sectional area - Площадь поперечного сечения трубы без деформации 0.01 m ^ 2 (по умолчанию) | положительный скаляр в единицах площади

Pipe wall specification - Определяет гибкость стен Rigid (по умолчанию) | Flexible

Зависимости

Hydraulic diameter - Эффективный диаметр некруглых труб 0.1128 m (по умолчанию) | положительный скаляр в единицах длины

Зависимости

Elevation gain specification - Задать свойство отметки трубы Constant (по умолчанию) | Variable

Elevation gain from port A to port B - Изменение высоты с порта A на порт B 0 m (по умолчанию) | положительный скаляр в единицах длины

Зависимости

Gravitational acceleration - Ускорение от силы тяжести на средней отметке трубы 9.81 m/s^2 (по умолчанию) | положительный скаляр в единицах длины/времени ^

Static pressure-diameter compliance - Измерение деформации трубы 1.2e-6 m/MPa (по умолчанию) | положительный скаляр в единицах длины/давления

Зависимости

Viscoelastic process time constant - Постоянная времени деформации трубы 0.01 s (по умолчанию) | положительный скаляр в единицах времени

Зависимости

Viscous friction parameterization - Модель трения Haaland correlation (по умолчанию) | Nominal pressure drop vs. nominal mass flow rate | Tabulated data - Darcy friction factor vs. Reynolds number

Aggregate equivalent length of local resistances - Незначительные потери давления в трубе, выраженные в виде длины 1 m (по умолчанию) | положительный скаляр в единицах длины

Зависимости

Internal surface absolute roughness - Абсолютная шероховатость стенки трубы 1.5e-5 m (по умолчанию) | положительный скаляр в единицах длины

Зависимости

Shape factor for laminar flow viscous friction - Постоянная трения для ламинарных потоков 64 (по умолчанию) | положительный безразмерный скаляр

Laminar flow upper Reynolds number limit - число Рейнольдса, ниже которого поток ламинарен 2e+3 (по умолчанию) | положительный безразмерный скаляр

Turbulent flow lower Reynolds number limit - число Рейнольдса, выше которого поток турбулентен 4e+3 (по умолчанию) | положительный безразмерный скаляр

Nominal mass flow rate - Массовый расход труб [0.1 1] kg/s (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Зависимости

Nominal pressure drop - Перепад давления над трубой [0.001 0.01] MPa (по умолчанию) | скаляр или вектор чисел в единицах давления

Зависимости

Mass flow rate threshold for flow reversal - Порог, ниже которого применяется численное сглаживание 1e-6 kg/s (по умолчанию) | положительный скаляр в единицах массы/времени

Зависимости

Зависимости

Зависимости

Nusselt number for laminar flow heat transfer - Номер Nusselt для использования в расчетах теплопередачи ламинарных потоков 3.66 (по умолчанию)

Зависимости

Nominal mass flow rate - Массовый расход труб [0.1 1] kg/s (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

Зависимости

Nominal inflow temperature - Температура на входе в трубопровод [293.15 293.15] K (по умолчанию) | скаляр или вектор чисел в единицах температуры

Зависимости

Nominal outflow temperature - Температура на выходе из трубы [300 300] K'(по умолчанию) | скаляр или вектор чисел в единицах температуры

Зависимости

Nominal inflow pressure - Давление на входе в трубопровод [0.101325 0.101325] MPa (по умолчанию) | скаляр или вектор чисел в единицах давления

Зависимости

Nominal wall temperature - Температура стенки трубы [303.15 303.15] K (по умолчанию) | скаляр или вектор чисел в единицах температуры

Зависимости

Coefficient a - Эмпирическая константа a корреляции Диттуса-Болтера 0.023 (по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent b - Эмпирическая константа b корреляции Диттуса-Болтера 0.8 (по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent c - Эмпирическая константа c корреляции Диттуса-Болтера 0.4 (по умолчанию) | положительный безразмерный скаляр

Зависимости

Зависимости

Colburn factor vector - Факторы Колберна, при которых табличные числа Рейнольдса [0.019 0.013 0.002] (по умолчанию) | вектор положительных безразмерных чисел

Зависимости

Зависимости

Prandtl number vector for Nusselt number - Числа Прандтля, для которых необходимо составить таблицу номера Нуссельта [1 10] (по умолчанию) | вектор положительных безразмерных чисел

Зависимости

Nusselt number table - Числа Нуссельта в табличных числах Рейнольдса и Прандтля [ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (по умолчанию) | матрица положительных безразмерных чисел

Зависимости

Initial liquid temperature - Абсолютная температура в трубе в начале моделирования 293.15 K (по умолчанию) | положительный скаляр или вектор в единицах измерения температуры

`EL` - Перепад отметок портов
физический сигнал

`A` - Открытие трубы
термическая жидкость

`B` - Открытие трубы
термическая жидкость

`H` - Трубная стена
тепловой

`Fluid dynamic compressibility` - Следует ли моделировать динамическую сжимаемость жидкости
`On` (по умолчанию) | `Off`

`Fluid inertia` - Следует ли моделировать ускорение жидкости
`On` (по умолчанию) | `Off`

`Number of segments` - Дискретизация труб
`1` (по умолчанию) | положительный безразмерный скаляр

`Pipe total length` - Общая длина трубы
`5 m` (по умолчанию) | положительный скаляр в единицах длины

`Nominal cross-sectional area` - Площадь поперечного сечения трубы без деформации
`0.01` m ^ 2 (по умолчанию) | положительный скаляр в единицах площади

`Pipe wall specification` - Определяет гибкость стен
`Rigid` (по умолчанию) | `Flexible`

`Hydraulic diameter` - Эффективный диаметр некруглых труб
`0.1128 m` (по умолчанию) | положительный скаляр в единицах длины

`Elevation gain specification` - Задать свойство отметки трубы
`Constant` (по умолчанию) | `Variable`

`Elevation gain from port A to port B` - Изменение высоты с порта A на порт B
`0 m` (по умолчанию) | положительный скаляр в единицах длины

`Gravitational acceleration` - Ускорение от силы тяжести на средней отметке трубы
`9.81 m/s^2` (по умолчанию) | положительный скаляр в единицах длины/времени ^

`Static pressure-diameter compliance` - Измерение деформации трубы
`1.2e-6 m/MPa` (по умолчанию) | положительный скаляр в единицах длины/давления

`Viscoelastic process time constant` - Постоянная времени деформации трубы
`0.01 s` (по умолчанию) | положительный скаляр в единицах времени

`Viscous friction parameterization` - Модель трения
`Haaland correlation` (по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

`Aggregate equivalent length of local resistances` - Незначительные потери давления в трубе, выраженные в виде длины
`1 m` (по умолчанию) | положительный скаляр в единицах длины

`Internal surface absolute roughness` - Абсолютная шероховатость стенки трубы
`1.5e-5 m` (по умолчанию) | положительный скаляр в единицах длины

`Shape factor for laminar flow viscous friction` - Постоянная трения для ламинарных потоков
`64` (по умолчанию) | положительный безразмерный скаляр

`Laminar flow upper Reynolds number limit` - число Рейнольдса, ниже которого поток ламинарен
`2e+3` (по умолчанию) | положительный безразмерный скаляр

`Turbulent flow lower Reynolds number limit` - число Рейнольдса, выше которого поток турбулентен
`4e+3` (по умолчанию) | положительный безразмерный скаляр

`Nominal mass flow rate` - Массовый расход труб
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

`Nominal pressure drop` - Перепад давления над трубой
`[0.001 0.01] MPa` (по умолчанию) | скаляр или вектор чисел в единицах давления

`Mass flow rate threshold for flow reversal` - Порог, ниже которого применяется численное сглаживание
`1e-6 kg/s` (по умолчанию) | положительный скаляр в единицах массы/времени

`Nusselt number for laminar flow heat transfer` - Номер Nusselt для использования в расчетах теплопередачи ламинарных потоков
`3.66` (по умолчанию)

`Nominal mass flow rate` - Массовый расход труб
`[0.1 1] kg/s` (по умолчанию) | скаляр или вектор чисел в единицах массы/времени

`Nominal inflow temperature` - Температура на входе в трубопровод
`[293.15 293.15] K` (по умолчанию) | скаляр или вектор чисел в единицах температуры

`Nominal outflow temperature` - Температура на выходе из трубы
`[300 300] K`'(по умолчанию) | скаляр или вектор чисел в единицах температуры

`Nominal inflow pressure` - Давление на входе в трубопровод
`[0.101325 0.101325] MPa` (по умолчанию) | скаляр или вектор чисел в единицах давления

`Nominal wall temperature` - Температура стенки трубы
`[303.15 303.15] K` (по умолчанию) | скаляр или вектор чисел в единицах температуры

`Coefficient a` - Эмпирическая константа a корреляции Диттуса-Болтера
`0.023` (по умолчанию) | положительный безразмерный скаляр

`Exponent b` - Эмпирическая константа b корреляции Диттуса-Болтера
`0.8` (по умолчанию) | положительный безразмерный скаляр

`Exponent c` - Эмпирическая константа c корреляции Диттуса-Болтера
`0.4` (по умолчанию) | положительный безразмерный скаляр

`Colburn factor vector` - Факторы Колберна, при которых табличные числа Рейнольдса
`[0.019 0.013 0.002]` (по умолчанию) | вектор положительных безразмерных чисел

`Prandtl number vector for Nusselt number` - Числа Прандтля, для которых необходимо составить таблицу номера Нуссельта
`[1 10]` (по умолчанию) | вектор положительных безразмерных чисел

`Nusselt number table` - Числа Нуссельта в табличных числах Рейнольдса и Прандтля
`[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ]` (по умолчанию) | матрица положительных безразмерных чисел

`Initial liquid temperature` - Абсолютная температура в трубе в начале моделирования
`293.15 K` (по умолчанию) | положительный скаляр или вектор в единицах измерения температуры

`Initial liquid pressure` - Абсолютное давление в трубе в начале моделирования
`0.101325 MPa` (по умолчанию) | положительный скаляр или вектор в единицах давления

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™