Регулируемое отверстие в изотермической аксиально-поршневой машине
Simscape/Жидкости/Изотермическая жидкость/Насосы и двигатели/Вспомогательные компоненты
Блок диафрагмы клапанной пластины (IL) моделирует отверстие в форме полумесяца между движущимися поршнями и насосом в аксиально-поршневой машине. Вращающиеся поршни периодически соединяются с входом или выходом насоса через диафрагму. К каждому цилиндру аксиально-поршневого насоса можно присоединить два блока клапанных пластин, представляющих собой как входной, так и выходной пазы насоса.
Вращающийся цилиндр с одной прорезью полумесяца соединен с впускным отверстием насоса в отверстии А и выпускным отверстием насоса в отверстии В. Эти точки соединены с пластиной между углом переноса давления и радиан (180 градусов) друг от друга. Угол поворота пластины задается сигналом в отверстии G. Угол положения цилиндра, γ, является суммой сигнала положения, G, и начального смещения угла, Фазовый угол, γ 0:
+ G.
γ всегда находится в диапазоне от 0 до 2δ. Для любого комбинированного сигнала и смещения, большего, чем 2δ рад, γ поддерживается на уровне 2λ, а для любого комбинированного сигнала и смещения ниже, чем 0 рад, и γ поддерживается на уровне 0. Чтобы изменить исходное положение отверстия относительно паза, можно настроить параметр Фазовый угол (Phase angle).
Аксиально-поршневая машина с пятью поршнями
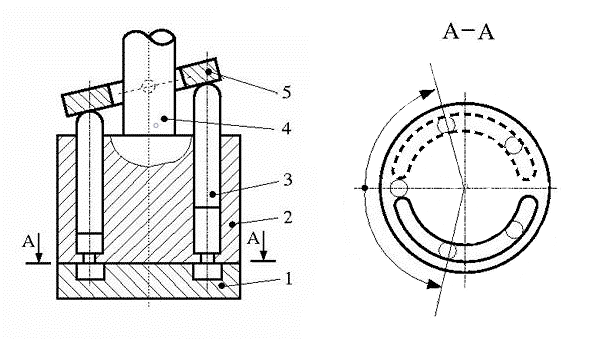
Цифры на диаграмме обозначают компоненты аксиально-поршневой машины:
Диафрагма клапанной пластины
Ротор
Поршень
Ведущий вал
Качающаяся пластина
Совмещение вращения цилиндра с пазом описывается следующими углами:
Угол цилиндра при повороте на паз, γ 1:
rR
Угол цилиндра при полном повороте на паз, γ 2:
rR
Угол цилиндра при повороте за паз, γ 3:
2rR
Угол цилиндра при полном повороте за паз, γ 4:
где:
Start- угол переноса давления. Этот угол представляет собой среднее угловое расстояние, которое поршень проходит в течение периода перехода давления от закрытого к открытому пазу.
r - половина диаметра отверстия цилиндра.
R - радиус шага блока цилиндров.
Расчеты площади диафрагмы при движении цилиндра
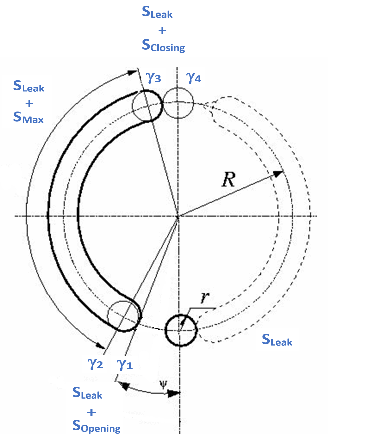
Площадь переходного отверстия, представляющего собой отверстие между углами γ 1 и γ 2 поворота цилиндра, рассчитывается следующим образом:
2βоткрытие)) + SLeak.
Площадь закрытия перехода, представляющая собой отверстие между углами γ 3 и γ 4 поворота цилиндра, рассчитывается как:
2βclosing)) + SLeak,
где параметры открытия и закрытия:
rR) − γ 2)),
и
− 2rR) 2)).
Площадь между γ 2 и γ 3 равна SLeak, а площадь между γ 4 и γ 1 SLeak.Максимальное отверстие SMax = ør2.
Ненулевой коэффициент сглаживания может обеспечить дополнительную численную стабильность, когда отверстие находится в почти закрытом или почти открытом положении.
На углах входа и выхода паза диафрагмы можно сохранить численную устойчивость при моделировании, настроив коэффициент сглаживания блока. Функция сглаживания применяется ко всем вычисленным углам, но в первую очередь влияет на моделирование в крайних точках этого диапазона.
Нормированный угол открытия перехода рассчитывается как:
− γ 1).
Коэффициент сглаживания s применяется к нормированному углу:
^ открыто − 1) 2 + (s4) 2.
Сглаженный угол открытия перехода составляет:
γ 2 − γ 1).
Аналогично, нормированный угол закрытия перехода равен:
− γ 3).
Коэффициент сглаживания s применяется к нормированному углу:
close − 1) 2 + (s4) 2.
Угол закрытия сглаженного перехода:
(γ 4 − γ 3)
Расход через отверстие клапанной пластины рассчитывается из соотношения давление-площадь:
где:
Cd - коэффициент разряда.
Aorifice - область, открытая для течения.
- средняя плотность текучей среды.
Δp - перепад давления над клапаном, ПА - ПБ.
Критическая разность давлений Δpcrit - это разность давлений, связанная с критическим числом Рейнольдса, Recrit, которое является точкой перехода между ламинарным и турбулентным потоком в жидкости:
2.