В данном примере описывается, как создать собственную библиотеку пользовательских блоков на основе файлов компонентов. В ней используется примерная библиотека моделей конденсаторов. Библиотека использует электрический домен Simscape™ Foundation и определяет три простых компонента. Дополнительные сведения, включая добавление нескольких уровней иерархии, добавление новых доменов и настройку внешнего вида библиотеки, см. в разделе История успеха - электрохимическая библиотека.
Библиотека примеров создается на вашем пути так, что она легко исполнима. Однако рекомендуется скопировать исходные файлы в новый каталог, для которого у вас есть разрешение на запись, и добавить этот каталог в путь MATLAB ®. Это позволит внести изменения и перестроить библиотеку под себя. Исходные файлы для библиотеки примеров находятся в следующем каталоге пакета :
matlabroot/toolbox/physmod/simscape/simscapedemos/+Capacitors
где matlabroot - корневой каталог MATLAB на компьютере, возвращаемый путем ввода
matlabroot
в окне команд MATLAB.
После копирования файлов измените имя каталога +Capacitors на другое имя, например +MyCapacitors, чтобы ваша копия библиотеки создавалась с уникальным именем.
Для построения библиотеки введите
ssc_build MyCapacitors
в окне команд MATLAB. Если здание из +MyCapacitors каталог пакета, вы можете опустить аргумент и тип просто
ssc_build
По завершении построения откройте созданную библиотеку, введя
MyCapacitors_lib
Дополнительные сведения о процессе построения библиотеки см. в разделе Создание пользовательских библиотек блоков.
Чтобы добавить блок, запишите соответствующий файл компонента и поместите его в каталог пакета. Например, блок идеального конденсатора в MyCapacitors_lib производится библиотекой IdealCapacitor.ssc файл. Откройте этот файл в редакторе MATLAB и проверьте его содержимое.
component IdealCapacitor
% Ideal Capacitor
% Models an ideal (lossless) capacitor. The output current I is related
% to the input voltage V by I = C*dV/dt where C is the capacitance.
% Copyright 2008-2017 The MathWorks, Inc.
nodes
p = foundation.electrical.electrical; % +:top
n = foundation.electrical.electrical; % -:bottom
end
parameters
C = { 1, 'F' }; % Capacitance
end
variables
i = { 0, 'A' }; % Current
v = {value = { 0, 'V' }, priority = priority.high}; % Voltage drop
end
branches
i : p.i -> n.i; % Through variable i from node p to node n
end
equations
assert(C > 0)
v == p.v-n.v; % Across variable v from p to n
i == C*v.der; % Capacitor equation
end
end
Сначала рассмотрим элементы файла компонента, влияющие на внешний вид блока. Дважды щелкните по блоку Ideal Capacitor в окне MyCapacitors_lib для открытия диалогового окна и сравнения значка блока и диалогового окна с содержимым IdealCapacitor.ssc файл. Название блока Ideal Capacitor взято из комментария на строке 2. Комментарии к строкам 3 и 4 затем используются для заполнения описания блока в диалоговом окне. Порты блока определяются секцией узлов. Выражения комментариев в конце каждой строки определяют метку порта и местоположение. Аналогично в разделе параметров комментарии используются для определения имен параметров в диалоговом окне блока. Дополнительные сведения см. в разделе Настройка имени и внешнего вида блока.
Также обратите внимание, что в разделе уравнений имеется утверждение, гарантирующее, что значение емкости всегда больше нуля. Это является хорошей практикой для обеспечения того, чтобы компонент не использовался вне области действия. В блоках библиотеки Simscape Foundation при необходимости выполняются такие проверки.
В данном примере библиотеки есть два дополнительных компонента, которые можно использовать для моделирования ultracapacitor. Эти компоненты являются эволюциями идеального конденсатора. Рекомендуется постепенно создавать модели компонентов, добавляя и тестируя дополнительные элементы по мере их добавления.
Идеальный Ultracapacitor
Ультраконденсаторы, как предполагает их название, являются конденсаторами с очень высоким значением ёмкости. Соотношение между напряжением и зарядом не является постоянным, в отличие от идеального конденсатора. Предположим, что в спецификации производителя представлен график емкости как функции напряжения, и что емкость увеличивается приблизительно линейно с напряжением от 1 фарада при нулевых вольтах до 1,5 фарада при напряжении 2,5 вольта. Если напряжение емкости обозначено v, то емкость может быть аппроксимирована как:
2· v
Для конденсатора ток i и напряжение v связаны стандартным уравнением
Cdvdt
и, следовательно,
) dvdt
где C0 = 1 и Cv = 0,2. Это уравнение реализуется следующей строкой в разделе уравнений файла Simscape IdealUltraCapacitor.ssc:
i == (C0 + Cv*v)*v.der;
Для того, чтобы программное обеспечение Simscape интерпретировало это уравнение, переменные (v и i) и параметры (C0 и Cv) должен быть определен в разделе объявления. Дополнительные сведения см. в разделах Объявление переменных компонентов и Объявление параметров компонентов.
Реализация некоторых уравнений компонентов требует использования внутренних переменных. Пример - при реализации ультраконденсатора с резистивными потерями. Существуют два резистивных члена, эффективное последовательное сопротивление R и сопротивление Rd саморазрядки. Из-за топологии невозможно непосредственно выразить уравнения конденсатора в терминах сквозных и поперечных переменных i и v.
Ultracapacitor с резистивными потерями
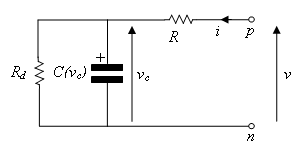
Этот блок реализуется файлом компонента LossyUltraCapacitor.ssc. Откройте этот файл в редакторе MATLAB и проверьте его содержимое.
component LossyUltraCapacitor
% Lossy Ultracapacitor
% Models an ultracapacitor with resistive losses. The capacitance C
% depends on the voltage V according to C = C0 + V*dC/dV. A
% self-discharge resistance is included in parallel with the capacitor,
% and an equivalent series resistance in series with the capacitor.
% Copyright 2008-2017 The MathWorks, Inc.
nodes
p = foundation.electrical.electrical; % +:top
n = foundation.electrical.electrical; % -:bottom
end
parameters
C0 = { 1, 'F' }; % Nominal capacitance C0 at V=0
Cv = { 0.2, 'F/V'}; % Rate of change of C with voltage V
R = {2, 'Ohm' }; % Effective series resistance
Rd = {500, 'Ohm' }; % Self-discharge resistance
end
variables
i = { 0, 'A' }; % Current
vc = {value = { 0, 'V' }, priority = priority.high}; % Capacitor voltage
end
branches
i : p.i -> n.i; % Through variable i from node p to node n
end
equations
assert(C0 > 0)
assert(R > 0)
assert(Rd > 0)
let
v = p.v-n.v; % Across variable v from p to n
in
i == (C0 + Cv*vc)*vc.der + vc/Rd; % Equation 1
v == vc + i*R; % Equation 2
end
end
end
Дополнительная переменная используется для обозначения напряжения на конденсаторе, vc. Затем уравнения могут быть выражены в терминах v, i и vc с использованием законов Кирхгофа о токе и напряжении. Суммирование токов на конденсаторе + узле даёт первое уравнение Симскейпа:
i == (C0 + Cv*vc)*vc.der + vc/Rd;
Суммирование напряжений даёт второе уравнение Симскейпа:
v == vc + i*R;
В качестве проверки количество уравнений, необходимых для компонента, используемого в одной соединённой сети, задается суммой числа портов плюс количество внутренних переменных минус один. Это не обязательно верно для всех компонентов (например, одно исключение - масса), но в целом это хорошее правило большого пальца. Здесь это дает 2 + 1 - 1 = 2.
В файле Simscape начальное условие (начальное напряжение в этом примере) применяется к переменной vc с priority = priority.high, потому что это дифференциальная переменная. В этом случае vc легко идентифицируется как дифференциальная переменная, поскольку она имеет der к нему применен оператор (дифференциатор).
Блоки конденсаторов в библиотеке примеров MyCapacitors_lib с ними связаны значки.

При построении библиотеки, если в каталоге имеется файл изображения с тем же именем, что и файл компонента Simscape, используется для определения значка блока. Например, блок идеального конденсатора, определяемый IdealCapacitor.ssc использует IdealCapacitor.jpg для определения значка блока. Если файл изображения не включен, то вместо значка блок отображает свое имя. Дополнительные сведения см. в разделе Настройка значка блока.