Изменяющееся во времени сопротивление потока
Двухфазная жидкость/элементы
Блок переменного локального ограничения (2P) моделирует падение давления из-за изменяющегося во времени сопротивления потока, такого как клапан. Порты A и B представляют собой входное и выходное отверстия ограничения. Порт AR устанавливает изменяющуюся во времени область ограничения, заданную как физический сигнал.
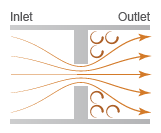
Ограничение состоит из сокращения с последующим внезапным расширением в области потока. Сжатие приводит к ускорению жидкости и падению ее давления. Расширение восстанавливает потерянное давление, хотя только частично, так как поток отделяется от стенки, теряя импульс в процессе.
Схема локального ограничения
Уравнение баланса массы
где:
и - массовый расход через порт A и порт B.
Уравнение энергетического баланса
= 0,
где:
A и B - это скорости потока энергии в ограничитель через порт A и порт B.
Предполагается, что локальное ограничение является адиабатическим, и поэтому изменение конкретной общей энтальпии равно нулю. В порту A,
pRstartR + wR22,
находясь в порту B,
pRstartR + wR22,
где:
uA, uB и uR являются специфическими внутренними энергиями в порту A, в порту B и ограничительной апертуре.
pA, pB и pR - давления в канале A, канале B и ограничительном отверстии.
A, В и R являются конкретными объемами в порте А, порте В и ограничительной апертуре.
wA, wB и wR являются идеальными скоростями потока в порту A, порту B и ограничительной апертуре.
Идеальная скорость потока вычисляется как
в порту A, как
в порту B и
внутри ограничения, где:
- идеальный массовый расход через ограничение.
S - площадь потока на порте A и порте B.
SR - площадь потока ограничительного отверстия.
Идеальный массовый расход через ограничение вычисляется как:
где:
КД - коэффициент расхода для локального ограничения.
Локальные переменные ограничения
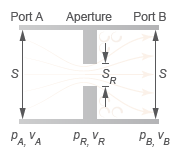
Изменение импульса между портами отражает потерю давления через ограничение. Эта потеря зависит от массового расхода через ограничение, хотя точная зависимость изменяется в зависимости от режима потока. При турбулентности потока:
pB 'startRKT,
где KT определяется как:
startout, RSRS),
в котором подстрочный индекс in обозначает входное отверстие и нижний индекс out выходное отверстие. Какой порт служит входом, а какой - выходом, зависит от перепада давления в ограничителе. Если давление в порту A больше, чем в порту B, то порт A является входным; если давление в отверстии B больше, то отверстие B является входным.
Когда поток ламинарный:
SRS) 2,
где ΔpTh обозначает пороговое падение давления, при котором поток начинает плавно переходить между ламинарным и турбулентным:
− BL),
в котором BLam является параметром блока отношения ламинарных давлений. Поток ламинарен, если перепад давления от порта A к порту B ниже порогового значения; в противном случае поток является турбулентным.
Давление в зоне ограничения pR также зависит от режима потока. При турбулентности потока:
− startв rsRSRS).
Когда поток ламинарный:
pB2.
Чтобы задать приоритет и начальные целевые значения для переменных блока перед моделированием, используйте вкладку «Переменные» в диалоговом окне блока (или раздел «Переменные» в Инспекторе свойств блока). Дополнительные сведения см. в разделе Установка приоритета и начальной цели для переменных блока.
Область по нормали к пути потока в ограничительном отверстии, когда ограничение находится в полностью закрытом состоянии. Площадь, полученная из физического сигнала AR, насыщается при этом значении. Входные значения, меньшие, чем минимальная область ограничения, игнорируются и заменяются указанным здесь значением. Значение по умолчанию 1e-10 м ^ 2.
Область по нормали к пути потока в ограничительном отверстии, когда ограничение находится в полностью открытом состоянии. Площадь, полученная из физического сигнала AR, насыщается при этом значении. Входные значения, превышающие максимальную область ограничения, игнорируются и заменяются указанным здесь значением. Значение по умолчанию: 0.005 м ^ 2.
Область по нормали к тракту потока в портах ограничения. Предполагается, что порты идентичны в поперечном сечении. Значение по умолчанию, 0.01 m ^ 2, совпадает с площадью ограничительной апертуры.
Отношение фактического к теоретическому массовому расходу через ограничение. Коэффициент разряда является эмпирическим параметром, используемым для учета неидеальных эффектов, таких как эффекты, обусловленные геометрией ограничения. Значение по умолчанию: 0.64.
Отношение давления на выходе к давлению на входе, при котором предполагается переключение режима потока с ламинарного на турбулентное. Преобладающий режим потока определяет уравнения, используемые при моделировании. Перепад давления через ограничение является линейным по отношению к массовому расходу, если поток ламинарный и квадратичный (по отношению к массовому расходу), если поток турбулентный. Значение по умолчанию: 0.999.
Пара двухфазных каналов для сохранения текучей среды, обозначенных А и В, представляет собой вход и выход ограничения. Порт ввода физического сигнала с меткой AR управляет площадью поперечного сечения ограничительной апертуры, расположенной между входным и выходным отверстиями ограничителя.