В этом учебном пособии показано, как моделировать управляемые гравитацией орбиты основных тел Солнечной системы. Модель рассматривает солнце и планеты как идеальные сферы с тремя поступательными степенями свободы. Вращение планеты игнорируется. Гравитационные поля генерируют силы, которые удерживают планеты на орбите.

Сферические твердотельные блоки представляют тела Солнечной системы и обеспечивают их геометрию, инерцию и цвета. Блоки декартового соединения определяют степени свободы тел относительно мирового каркаса, расположенного в барицентре Солнечной системы. Блоки гравитационного поля добавляют силы дальнего действия, ответственные за изгиб начальных траекторий планет на замкнутые эллиптические орбиты.
Блоки декартового соединения обеспечивают начальные состояния - положения и скорости - Солнца и планет относительно мирового каркаса. Начальные состояния соответствуют конфигурации Солнечной системы 20 июня 2016 года. Они получены из баз данных эфемерид, которые ведутся Лабораторией реактивного движения (JPL).
С помощью веб-интерфейса или интерфейса telnet можно запрашивать базы данных через систему JPL Horizons. Пользователи Aerospace Toolbox могут также получить данные ephemeris в командной строке MATLAB ® с помощью planetEphemeris после установки пакета поддержки Aerospace Ephemeris Data.
Откройте шаблон модели Simscape™ Multibody™ и удалите все ненужные блоки. Измените настройки силы тяжести, чтобы можно было добавить гравитационные поля в модель. Результат является отправной точкой для модели Солнечной системы.
В командной строке MATLAB введите smnew. MATLAB открывает шаблон модели с часто используемыми блоками и подходящими настройками решателя для моделей Simscape Multibody.
Вырезать все блоки, кроме «Конфигурация механизма» (Mechanism Configuration), «Конфигурация решателя» (Solver Configuration) и «Мировой кадр» (World Frame). Эти три блока предоставляют модели настройки силы тяжести, настройки решателя и систему координат глобальной инерции.
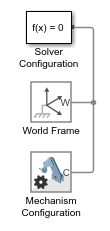
В диалоговом окне Блок конфигурации механизма (Mechanism Configuration block) задайте для параметра Равномерная сила тяжести (Uniform Gravity None. Этот параметр позволяет моделировать гравитацию как обратную квадратную силу закона с использованием блоков гравитационного поля.
Представление тел Солнечной системы с помощью блоков Сферическое тело (Spherical Solid). Задайте параметры геометрии и инерции в терминах переменных MATLAB и инициализируйте эти переменные в рабочем пространстве модели с помощью Проводника моделей. Переменные представляют собой структуры данных, названные в честь тел Солнечной системы с использованием собственной существительной капитализации.
Добавьте в модель девять блоков сферического тела из библиотеки элементов тела. Блоки представляют Солнце и восемь известных планет.
Подключите блоки и присвойте им имя, как показано на рисунке. Разветвленная рамная соединительная линия между мировой рамой и планетами делает их жестко связанными и совпадающими в пространстве. Позднее это условие можно изменить с помощью декартовых блоков соединения.
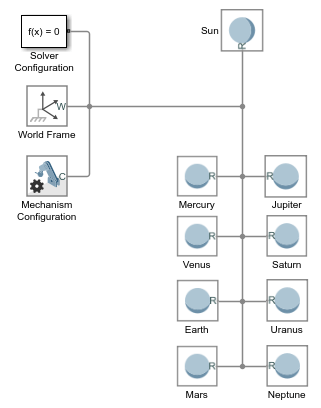
В диалоговых окнах блока «Сферическое тело» задайте для параметра «Инерция > На основе» значение Mass. Параметр инерции позволяет задать массу твердого тела непосредственно, чтобы можно было масштабировать формы планеты, не влияя на динамику модели.
Задайте следующие параметры блока Сферическое тело (Spherical Solid) в терминах полей структуры данных MATLAB. Введите имена полей в формате Structure.Field, где Structure - название в заглавном регистре тела Солнечной системы, а Field - строка, показанная в таблице, например ,Sun.R или Earth.RGB.
| Параметр блока | Строка поля |
|---|---|
| Геометрия > Радиус | R |
| Инерция > Масса | M |
| Графика > Визуальные свойства > Цвет | RGB |
Новые поля структуры позднее определяются в рабочем пространстве модели с помощью Проводника моделей.
На вкладке Моделирование (Modeling) щелкните Обозреватель моделей (Model Explorer).
На панели Иерархия модели (Model Hierarchy) Проводника моделей (Model Explorer) разверните узел модели и выберите Модель (Model) Рабочее пространство (Workspace). Панель Иерархия модели (Model Hierarchy) находится слева.
На панели «Рабочее пространство модели» Проводника моделей задайте для параметра «Источник данных» значение MATLAB Code. Панель Рабочее пространство модели (Model Workspace) находится справа.
В поле MATLAB Code добавьте код инициализации для свойств твердого тела солнца и планеты. Код организован в разделы, названные в честь тел Солнечной системы. Позже к этим разделам добавляются данные о начальной позиции и скорости.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8];
Щелкните Повторно инициализировать из источника.
Блоки сферического тела теперь имеют все числовые данные, необходимые для визуализации форм и цветов планет. Попробуйте открыть диалоговое окно Сферический твердотельный блок (Spherical Solid block) и убедитесь, что сфера теперь отображается на панели визуализации твердого тела.
Визуализация твердого тела Земли

Добавьте три поступательные степени свободы между барицентром Солнечной системы и каждым телом Солнечной системы, используя блоки декартового соединения. Эти блоки позже используются для задания начальных положений и скоростей тел Солнечной системы.
Добавьте в модель девять декартовых блоков соединений из библиотеки «Соединения». Блоки обеспечивают поступательные степени свободы Солнца и восьми известных планет.
Подключите блоки и присвойте им имя, как показано на рисунке. При размещении блока на существующей соединительной линии программа Simscape Multibody автоматически подключает блок к этой линии. Переверните и поверните соединительные блоки, чтобы обеспечить соединение сферических твердотельных блоков только с портами рамы толкателя (F).
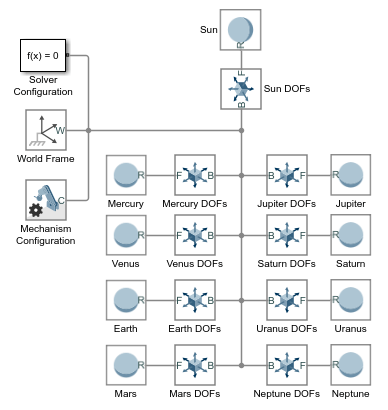
Солнце и планеты уже не связаны жестко. Теперь они могут переводить относительно друг друга. Однако они все еще совпадают в пространстве. Чтобы разместить их на разных начальных позициях и дать им начальные скорости, необходимо указать цели совместного состояния.
Укажите начальные состояния солнца и планеты с помощью переменных MATLAB, используя блоки декартового соединения в модели. Затем инициализируйте новые переменные MATLAB в рабочем пространстве модели с помощью Проводника моделей. Переменные MATLAB определяются как новые поля в существующих структурах данных.
В диалоговых окнах блока «Декартово соединение» установите флажки «Цели состояния» > «Указать цель положения» и «Цели состояния» > «Указать цель скорости» для призматических примитивов соединения X, Y и Z. Эти параметры позволяют задать требуемые начальные состояния Солнца и планет.
Задайте целевые значения состояния декартового соединения для примитивов призматического соединения X, Y и Z в терминах полей структуры MATLAB. Введите имена полей в формате Structure.Field, где Structure - название в заглавном регистре тела Солнечной системы, а Field - строка, показанная в таблице, например ,Sun.Px или Earth.Vz.
| Примитивная ось соединения | Целевой объект состояния | Строка поля |
|---|---|---|
| X | Положение | Px |
| Скорость | Vx | |
| Y | Положение | Py |
| Скорость | Vy | |
| Z | Положение | Pz |
| Скорость | Vz |
Новые поля структуры позднее определяются в рабочем пространстве модели с помощью Проводника моделей.
На вкладке Моделирование (Modeling) щелкните Обозреватель моделей (Model Explorer).
На панели Иерархия модели (Model Hierarchy) Проводника Mechanics разверните узел модели и выберите Модель (Model) Рабочая область (Workspace). Панель Иерархия модели (Model Hierarchy) находится слева.
На панели «Рабочее пространство модели» Проводника моделей задайте для параметра «Источник данных» значение MATLAB Code. Панель Рабочее пространство модели (Model Workspace) находится справа.
В поле MATLAB Code добавьте код инициализации для целей совместного состояния. Новый код, показанный синим цветом, состоит из компонентов позиции и скорости, полученных из баз данных ephemeris JPL. Можно скопировать только новый код или заменить весь код рабочей области модели.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; Sun.Px = 5.5850e+08; Sun.Py = 5.5850e+08; Sun.Pz = 5.5850e+08; Sun.Vx = -1.4663; Sun.Vy = 11.1238; Sun.Vz = 4.8370; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; Mercury.Px = 5.1979e+10; Mercury.Py = 7.6928e+09; Mercury.Pz = -1.2845e+09; Mercury.Vx = -1.5205e+04; Mercury.Vy = 4.4189e+04; Mercury.Vz = 2.5180e+04; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; Venus.Px = -1.5041e+10; Venus.Py = 9.7080e+10; Venus.Pz = 4.4635e+10; Venus.Vx = -3.4770e+04; Venus.Vy = -5.5933e+03; Venus.Vz = -316.8994; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; Earth.Px = -1.1506e+09; Earth.Py = -1.3910e+11; Earth.Pz = -6.0330e+10; Earth.Vx = 2.9288e+04; Earth.Vy = -398.5759; Earth.Vz = -172.5873; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; Mars.Px = -4.8883e+10; Mars.Py = -1.9686e+11; Mars.Pz = -8.8994e+10; Mars.Vx = 2.4533e+04; Mars.Vy = -2.7622e+03; Mars.Vz = -1.9295e+03; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; Jupiter.Px = -8.1142e+11; Jupiter.Py = 4.5462e+10; Jupiter.Pz = 3.9229e+10; Jupiter.Vx = -1.0724e+03; Jupiter.Vy = -1.1422e+04; Jupiter.Vz = -4.8696e+03; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; Saturn.Px = -4.2780e+11; Saturn.Py = -1.3353e+12; Saturn.Pz = -5.3311e+11; Saturn.Vx = 8.7288e+03; Saturn.Vy = -2.4369e+03; Saturn.Vz = -1.3824e+03; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; Uranus.Px = 2.7878e+12; Uranus.Py = 9.9509e+11; Uranus.Pz = 3.9639e+08; Uranus.Vx = -2.4913e+03; Uranus.Vy = 5.5197e+03; Uranus.Vz = 2.4527e+03; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8]; Neptune.Px = 4.2097e+12; Neptune.Py = -1.3834e+12; Neptune.Pz = -6.7105e+11; Neptune.Vx = 1.8271e+03; Neptune.Vy = 4.7731e+03; Neptune.Vz = 1.9082e+03;
Щелкните Повторно инициализировать из источника.
Теперь модель имеет численные данные, необходимые для сборки планет в координатах положения, полученных из баз данных JPL. Однако моделирование модели в этой точке показало бы, что планеты движутся по прямолинейным траекториям. Чтобы получить эллиптические орбиты, необходимо завершить модель, добавив гравитационные поля солнца и планеты.
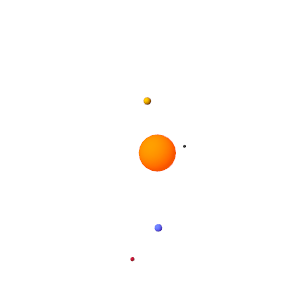
Моделирование гравитационного натяжения каждого тела Солнечной системы с помощью блока Гравитационное поле (Gravitational Field). Этот блок автоматически вычисляет гравитационное вытягивание тела на все другие тела, используя закон всеобщего тяготения Ньютона.
В каждом диалоговом окне «Сферический твердотельный блок» разверните область «Рамки» и нажмите кнопку «Создать».
Задайте для параметра «Имя кадра» значение R2 и нажмите кнопку «Сохранить». Новый кадр является точной копией опорного кадра, но имеет отдельный порт кадра. Эти порты можно использовать для соединения блоков гравитационного поля, избегая при этом пересекающихся линий соединения.
Добавьте к модели девять блоков гравитационного поля из библиотеки сил и крутящих моментов. Блоки обеспечивают гравитационные силы, которые каждое тело Солнечной системы оказывает на все другие тела.
Подключите блоки и присвойте им имя, как показано на рисунке. Убедитесь, что блоки соединены непосредственно с блоками сферического тела. Такое соединение гарантирует, что поля центрированы на твердых сферах и жестко соединены с ними.
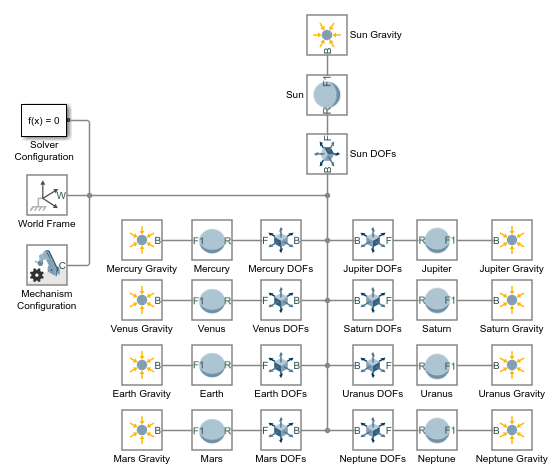
В блоках «Гравитационное поле» задайте параметр «Масса» в качестве имен полей структуры MATLAB. Введите имена полей в формате Structure.Field, где Structure - название тела Солнечной системы, а Field - строка M— например, Sun.M или Earth.M. Эти поля были предварительно определены в рабочей области модели.
Настройте параметры решателя Simulink ®, чтобы зафиксировать десять оборотов земли в одном моделировании. Затем смоделируйте модель и просмотрите полученную анимацию Солнечной системы. Настройте параметры анимации для воспроизведения десятилетней анимации в течение нескольких секунд.
Откройте окно Параметры конфигурации (Configuration Parameters). На вкладке Моделирование (Modeling) щелкните Параметры модели (Model Settings).
Установите для параметра Stop time значение 10*365*24*60*60. Это число, равное десяти годам в секундах, позволяет смоделировать полные десять земных оборотов с 20 июня 2016 года по 20 июня 2026 года.
Задайте для параметра Max step size значение 24*60*60. Это число, равное одному дню в секундах, достаточно мало, чтобы обеспечить плавные результаты анимации. Увеличьте это число, если хотите получить более быстрые результаты моделирования.
Обновите блок-схему. На вкладке Моделирование (Modeling) щелкните Обновить модель (Update Model). Откроется Mechanics Explorer со статическим 3-D отображением модели в ее исходном состоянии. Убедитесь, что солнце и планеты отображаются на панели визуализации и что их относительные размеры и положения являются разумными.
Запустите моделирование.. Mechanics Explorer воспроизводит анимацию Солнечной системы. Обратите внимание, что при базовой скорости воспроизведения по умолчанию планеты выглядят статическими. Необходимо увеличить эту скорость в настройках анимации Проводника Mechanics.
В Обозревателе Mechanics выберите «Сервис» > «Настройки анимации».
В поле «Базовая (1X) скорость воспроизведения» введите3153600. Эта скорость соответствует одному обороту земли каждые десять секунд.
Приостановите и воспроизведите анимацию, чтобы применить новую базовую скорость воспроизведения. На рисунке показаны результаты анимации с новой скоростью.
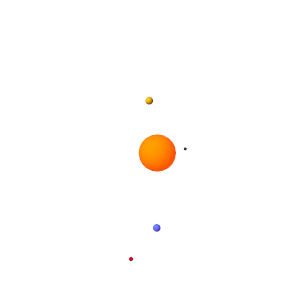
Можно открыть полную модель Солнечной системы, введя smdoc_solar_system_wfield_b в командной строке MATLAB.