Обратная рекурсия Левинсона - Дурбина
r = rlevinson(a,efinal)
[r,u] = rlevinson(a,efinal)
[r,u,k] = rlevinson(a,efinal)
[r,u,k,e] = rlevinson(a,efinal)
Обратная рекурсия Левинсона - Дурбина реализует пошаговый алгоритм решения следующей симметричной системы Тёплица линейных уравнений для r, где r = [r (1 )... r ( p + 1)] и r (i) * обозначает комплексный конъюгат r (i).
+ 1)] = [− r (2) − r (3) ⋮−r (p + 1)]
r = rlevinson(a,efinal) решает вышеуказанную систему уравнений для r данного вектора a, где a = [1 a (2 )... a ( p + 1)]. В приложениях линейного прогнозированияr представляет собой автокорреляционную последовательность входа в фильтр ошибок прогнозирования, где r (1) - элемент с нулевым запаздыванием. На рисунке ниже показан типичный фильтр этого типа, где H (z) является оптимальным линейным предиктором, x (n) является входным (n) является прогнозируемым сигналом, и e (n) является ошибкой предсказания.
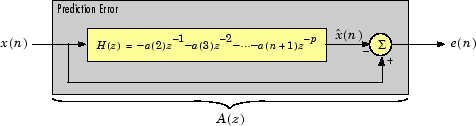
Входной вектор а представляет полиномиальные коэффициенты этого фильтра ошибок прогнозирования в степени убывания z.
(n + 1) z − p
Для создания допустимой автокорреляционной последовательности фильтр должен быть минимально-фазовым. efinal - мощность ошибки скалярного предсказания, которая равна дисперсии сигнала ошибки предсказания, start2 (e).
[r,u] = rlevinson(a,efinal) возвращает верхнюю треугольную матрицу U из разложения UDU *
где
∗⋮⋱⋱⋮r (p) ⋯r (2) r (1)]
и E - диагональная матрица с элементами, возвращенными на выходе e (см. ниже). Это разложение позволяет эффективно оценивать обратную автокорреляционную матрицу, R − 1.
Выходная матрица u содержит полином фильтра прогнозирования, a, из каждой итерации обратной рекурсии Левинсона-Дурбина
∗⋮⋱⋱⋮0⋯0ap+1 (1) ∗]
где ai (j) - j-й коэффициент полинома фильтра предсказания i-го порядка (т.е. шаг i в рекурсии). Например, полином фильтра прогнозирования 5-го порядка является
a5 = u(5:-1:1,5)'
Обратите внимание, что u(p+1:-1:1,p+1)' - вектор входного полиномиального коэффициента a.
[r,u,k] = rlevinson(a,efinal) возвращает вектор k длины p + 1, содержащей коэффициенты отражения. Коэффициенты отражения являются сопряжениями значений в первой строке u.
k = conj(u(1,2:end))
[r,u,k,e] = rlevinson(a,efinal) возвращает вектор длиной p + 1, содержащий ошибки предсказания из каждой итерации обратной рекурсии Левинсона-Дурбина: e(1) - ошибка прогнозирования из модели первого порядка, e(2) ошибка прогнозирования из модели второго порядка и т.д.
Эти значения ошибки предсказания формируют диагональ матрицы E в разложении UDU * на R − 1.
Оцените спектр двух синусоидальных волн в шуме с помощью авторегрессионной модели. Выберите наилучший порядок моделей из группы моделей, возвращаемых обратной рекурсией Левинсона-Дурбина.
Создайте сигнал. Укажите частоту дискретизации 1 кГц и длительность сигнала 50 секунд. Синусоиды имеют частоты 50 Гц и 55 Гц. Шум имеет дисперсию 0,2 ².
Fs = 1000; t = (0:50e3-1)'/Fs; x = sin(2*pi*50*t) + sin(2*pi*55*t) + 0.2*randn(50e3,1);
Оцените параметры авторегрессионной модели.
[a,e] = arcov(x,100); [r,u,k] = rlevinson(a,e);
Оцените спектральную плотность мощности для порядков 1, 5, 25, 50 и 100.
N = [1 5 25 50 100]; nFFT = 8096; P = zeros(nFFT,5); for idx = 1:numel(N) order = N(idx); ARtest = flipud(u(:,order)); P(:,idx) = 1./abs(fft(ARtest,nFFT)).^2; end
Постройте график оценок PSD.
F = (0:1/nFFT:1/2-1/nFFT)*Fs; plot(F, 10*log10(P(1:length(P)/2,:))) grid legend([repmat('Order = ',[5 1]) num2str(N')]) xlabel('Frequency (Hz)') ylabel('dB') xlim([35 70])
[1] Кей, Стивен М. Современная спектральная оценка: теория и применение. Энглвуд Клиффс, Нью-Джерси: Прентис-Холл, 1988.