Проектирование

Возмущение решения решателем состояний системы для лучшего удовлетворения отношений инвариантного по времени решения

Необходимый

Нет

Язык

MATLAB

Синтаксис

Projection(s)

Аргументы

s: Экземпляр Simulink.MSFcnRunTimeBlock класс, представляющий Уровень 2 MATLAB S-Function block.

Описание

Этот способ предназначен для использования с S-функциями, которые моделируют динамические системы, состояния которых удовлетворяют временным инвариантным соотношениям, таким как те, которые являются результатом сохранения массы или энергии или других физических законов. Модуль Simulink ® вызывает этот метод на каждом временном шаге после того, как решатель модели вычислит состояния S-функции для этого временного шага. Обычно небольшие ошибки в числовом решении состояний приводят к тому, что решения не удовлетворяют инвариантам решения в точности. ВашProjection способ может компенсировать ошибки путем возмущения состояний так, чтобы они более близко приближали инварианты решения на текущем временном шаге. В результате численное решение по мере продвижения моделирования более тесно согласуется с идеальным решением, обеспечивая более точное общее моделирование системы, смоделированной с помощью S-функции.

Ваш Projection возмущения системного состояния метода должны находиться в пределах допусков ошибок решения, заданных моделью, в которую встроена S-функция. В противном случае возмущения могут сделать решение решателя недействительным. Это зависит от вашего Projection для обеспечения соответствия возмущений допускам ошибок, заданным моделью. Простой метод возмущения состояний системы см. в разделе Состояния системы с использованием инварианта решения. В следующих статьях описаны более сложные методы возмущения, которые mdlProjection способ может быть использован.

C.W. Gear, «Поддержание инвариантов решения в числовом решении ОДУ», Journal on Scientific and Statistical Computing, Vol. 7, No. 3, July 1986.
Л. Ф. Шампин, «Законы сохранения и числовое решение ОДУ I», Компьютеры и математика с приложениями, т. 12B, 1986, стр. 1287-1296.
Л. Ф. Шампин, «Законы сохранения и числовое решение ОДУ II», Computers and Mathematics with Applications, Vol. 38, 1999, pp. 61-72.

Пример

Состояния системы Perturb с использованием инварианта решения

Вот простой, основанный на серии Тейлора подход к возмущению состояний системы. Предположим, что ваша S-функция моделирует динамическую систему, имеющую инвариант решения, $g (X,$ t), т.е. g является непрерывной, дифференцируемой функцией состояний системы, X и времени $,$ t, значение которой является постоянным со временем. Тогда

$_{}_{}^{}_{}^{Xn≅Xn*+JnT} {(_{}_{}^{} JnJnT}^{)} -_{}$ 1Rn

где

$_{Xn}$ - вектор идеального состояния системы на текущем шаге времени решателя;
$_{Xn}^{}$ * - приближенный вектор состояния, вычисленный решателем на текущем шаге времени
$_{Jn}$ - якобиан инвариантной функции, оцениваемый в точке пространства состояний, заданной вектором приближенного состояния на текущем шаге времени:
$_{} \frac{}{Jn=∂g∂X} (_{}^{Xn}_{*,}$ tn)
$_{tn}$ - время на текущем шаге времени
$_{Rn}$ представляет собой остаток (разность) между инвариантной функцией, оцениваемой при $_{Xn}$ и $_{Xn}^{}$ * на текущем временном шаге:
$_{Rn} = g_{} (_{Xn}, tn)_{}^{-} g_{} ($ Xn *, tn)
Примечание
Величина $g (_{} Xn,_{}$ tn) одинакова на каждом временном этапе и известна по определению.

Учитывая непрерывную, дифференцируемую инвариантную функцию для системы, которую моделирует ваша S-функция, эта формула позволяет вашей S-функции mdlProjection способ вычисления возмущения

$_{}^{JnT} {(_{}_{}^{} JnJnT}^{)} -_{}$ 1Rn

числового решения решателя Xn $_{}^{}$ *, которое более точно соответствует идеальному решению Xn, $_{}$ удерживая решение S-функции от дрейфа от идеального решения по мере продвижения моделирования.

Пример MATLAB

Этот пример иллюстрирует, как метод возмущений, описанный в предыдущем разделе, может удерживать численное решение модели от дрейфа от идеального решения в процессе моделирования. Рассмотрим следующие model,mdlProjectionEx1:

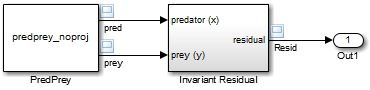
Блок PredPrey ссылается на S-функцию, predprey_noproj.m, который использует уравнения Лотка-Вольтерра

$\begin{array}{l} \overset{}{} x˙=ax (1 - \\ \overset{y}{}) y˙=−cy \end{array}$ (1 − x)

для моделирования динамики популяции хищника-добычи, где $x (t$ ) - плотность популяции хищников, а $y ($ t) - плотность популяции добычи. Идеальное решение ODE хищника-добычи удовлетворяет инвариантной во времени функции

$x^{-}^{}^{cecxy}^{-}$ aeay = d

где $a$ , $c$ и $d$ - константы. S-функция предполагает a = 1, c = 2, и d = 121.85.

Блок Инвариантный остаток (Invariant Resident) в этой модели вычисляет остаток между инвариантной функцией, оцениваемой вдоль идеальной траектории системы через пространство состояний, и ее моделируемой траекторией:

$_{Rn} = d_{}^{-}^{xn_{-}}_{}^{}^{_{cecxnyn}}$ − aeayn

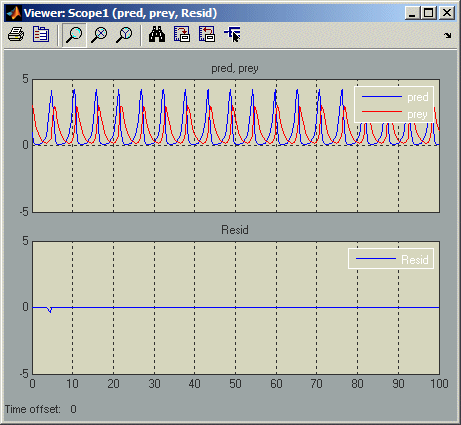
где $_{}$ xnand $_{}$ ynare значения, вычисленные решателем модели для плотности популяции хищника и добычи, соответственно, на текущем шаге времени. В идеале остаток должен быть равен нулю на протяжении всего моделирования модели, но моделирование модели показывает, что остаток на самом деле значительно отклоняется от нуля:

Рассмотрим следующую модель, mdlProjectionEx2:

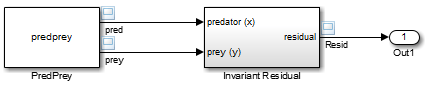
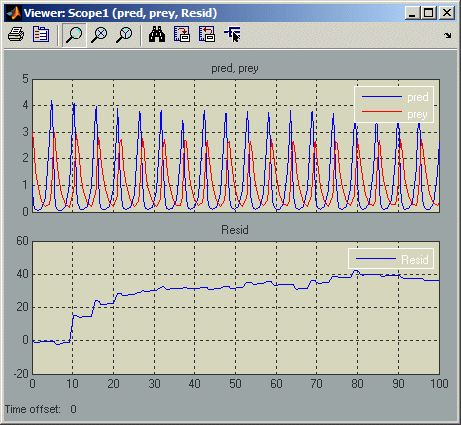
Эта модель аналогична предыдущей, за исключением ее S-функции, predprey.m, включает mdlProjection метод, который использует подход возмущений, описанный в Perturb System Stations Using a Solution Invariant для компенсации численного дрейфа. В результате численное решение более точно отслеживает идеальное решение по мере продвижения моделирования, как показано остаточным сигналом, который остается близким или равным нулю на протяжении всего моделирования:

См. также

Simulink.MSFcnRunTimeBlock, mdlProjection,

Представлен в R2012b

Документация