В этом примере показано, как подгонять обобщенную линейную модель смешанных эффектов (GLME) к данным выборки.
Загрузите образцы данных.
load mfr
Производственная компания управляет 50 фабриками по всему миру, и каждая из них выполняет пакетный процесс для создания готового продукта. Компания хочет уменьшить количество дефектов в каждой партии, поэтому разработала новый производственный процесс. Тем не менее, компания хочет протестировать новый процесс на отдельных фабриках, чтобы убедиться в его эффективности перед развертыванием во всех 50 местоположениях.
Чтобы проверить, значительно ли новый процесс уменьшает количество дефектов в каждой партии, компания выбрала 20 своих заводов случайным образом для участия в эксперименте. Десять фабрик внедрили новый процесс, а другие десять использовали старый процесс.
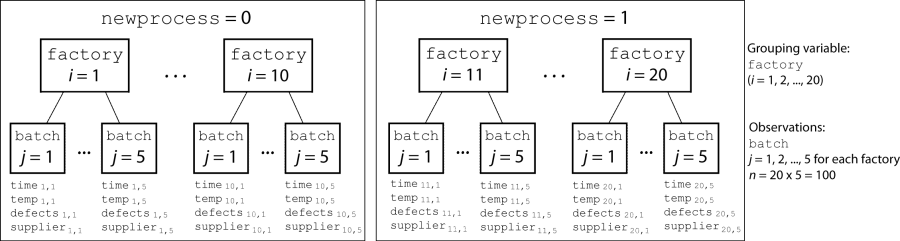
На каждом из 20 заводов (i = 1, 2,..., 20) компания провела пять партий (j = 1, 2,..., 5) и записала в таблицу следующие данные: mfr:
Флаг для указания использования нового процесса:
Если партия использовала новый процесс, то newprocess = 1
Если в партии использовался старый процесс, то newprocess = 0
Время обработки партии, в часах (time)
Температура партии, в градусах Цельсия (temp)
Поставщик химического вещества, используемого в партии (supplier)
supplier - категориальная переменная с уровнями A, B, и C, где каждый уровень представляет одного из трех поставщиков
Количество дефектов в партии (дефекты)
Данные также включают time_dev и temp_dev, которые представляют собой абсолютное отклонение времени и температуры, соответственно, от технологического стандарта 3 часов и 20 градусов Цельсия. Переменная ответа defects имеет распределение Пуассона. Это смоделированные данные.
Компания должна определить, позволяет ли новый процесс значительно сократить количество дефектов в каждой партии, с учетом различий в качестве, которые могут существовать из-за специфичных для завода изменений во времени, температуре и поставщике. Количество дефектов в партии может быть смоделировано с использованием распределения яда:
мкидж)
Используйте обобщенную линейную модель смешанных эффектов для моделирования количества дефектов в партии:
β5supplier _ Bij + bi,
где
defectsij - количество дефектов, наблюдаемых в партии, произведенной заводом i во время партии j.
pciij - среднее число дефектов, соответствующих заводу i (где i = 1, 2,..., 20) во время партии j (где j = 1, 2,..., 5).
newprocessij, time_devij и temp_devij являются измерениями для каждой переменной, которые соответствуют фабрике i во время партии j. Например, newprocessij указывает, использовала ли партия, произведенная заводом i во время партии j, новый процесс.
supplier_Cij и supplier_Bij являются фиктивными переменными, которые используют кодирование эффектов (сумма к нулю), чтобы указать, C или B, соответственно, поставлялись технологические химикаты для партии, произведенной заводом i во время партии j.
bi ~ N (0, startb2) - перехват случайных эффектов для каждой фабрики i, который учитывает специфичные для фабрики вариации качества.
Подгонка обобщенной линейной модели смешанных эффектов с использованием newprocess, time_dev, temp_dev, и supplier в качестве предикторов с фиксированными эффектами. Включить термин случайных эффектов для перехвата, сгруппированного по factory, чтобы учесть различия в качестве, которые могут существовать из-за специфичных для завода вариаций. Переменная ответа defects имеет распределение Пуассона, и соответствующей функцией связи для этой модели является log. Для оценки коэффициентов используется метод аппроксимации Лапласа. Укажите фиктивную кодировку переменной как 'effects'так что фиктивные переменные коэффициенты суммируются до 0.
glme = fitglme(mfr,... 'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',... 'Distribution','Poisson','Link','log','FitMethod','Laplace',... 'DummyVarCoding','effects')
glme =
Generalized linear mixed-effects model fit by ML
Model information:
Number of observations 100
Fixed effects coefficients 6
Random effects coefficients 20
Covariance parameters 1
Distribution Poisson
Link Log
FitMethod Laplace
Formula:
defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1 | factory)
Model fit statistics:
AIC BIC LogLikelihood Deviance
416.35 434.58 -201.17 402.35
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
'(Intercept)' 1.4689 0.15988 9.1875 94 9.8194e-15
'newprocess' -0.36766 0.17755 -2.0708 94 0.041122
'time_dev' -0.094521 0.82849 -0.11409 94 0.90941
'temp_dev' -0.28317 0.9617 -0.29444 94 0.76907
'supplier_C' -0.071868 0.078024 -0.9211 94 0.35936
'supplier_B' 0.071072 0.07739 0.91836 94 0.36078
Lower Upper
1.1515 1.7864
-0.72019 -0.015134
-1.7395 1.5505
-2.1926 1.6263
-0.22679 0.083051
-0.082588 0.22473
Random effects covariance parameters:
Group: factory (20 Levels)
Name1 Name2 Type Estimate
'(Intercept)' '(Intercept)' 'std' 0.31381
Group: Error
Name Estimate
'sqrt(Dispersion)' 1 Model information таблица отображает общее количество наблюдений в данных выборки (100), количество коэффициентов фиксированных и случайных эффектов (6 и 20 соответственно) и количество параметров ковариации (1). Это также указывает, что переменная ответа имеет Poisson распределение, функция линии связи Log, и метод подгонки Laplace.
Formula указывает спецификацию модели с помощью нотации Уилкинсона.
Model fit statistics В таблице представлены статистические данные, используемые для оценки соответствия модели. Это включает в себя информационный критерий Акаике (AIC), байесовский информационный критерий (BIC) значения, логарифмическое правдоподобие (LogLikelihood) и отклонение (Deviance) значения.
Fixed effects coefficients таблица показывает, что fitglme возвращены 95% доверительные интервалы. Он содержит одну строку для каждого предиктора с фиксированными эффектами, и каждый столбец содержит статистику, соответствующую этому предиктору. Столбец 1 (Name) содержит имя каждого коэффициента с фиксированными эффектами, столбец 2 (Estimate) содержит его оценочное значение и столбец 3 (SE) содержит стандартную ошибку коэффициента. Колонка 4 (tStat) содержит t-статистику для проверки гипотезы, что коэффициент равен 0. Столбец 5 (DF) и колонку 6 (pValue) содержат степени свободы и p-значение, которые соответствуют t-статистике соответственно. Последние два столбца (Lower и Upper) отображать нижний и верхний пределы, соответственно, 95% доверительного интервала для каждого коэффициента с фиксированными эффектами.
Random effects covariance parameters отображает таблицу для каждой переменной группировки (здесь, только factory), включая его общее количество уровней (20), и тип и оценку параметра ковариации. Здесь, std указывает, что fitglme возвращает стандартное отклонение случайного эффекта, связанного с заводским предиктором, которое имеет оценочное значение 0,31381. Также отображается таблица, содержащая тип параметра ошибки (здесь квадратный корень параметра дисперсии) и его оценочное значение 1.
Стандартный экран, созданный fitglme не обеспечивает доверительные интервалы для параметров случайных эффектов. Для вычисления и отображения этих значений используйте covarianceParameters.
Чтобы определить, сгруппирован ли перехват случайных эффектов по factory является статистически значимым, вычислить доверительные интервалы для оцененного параметра ковариации.
[psi,dispersion,stats] = covarianceParameters(glme);
covarianceParameters возвращает оцененный параметр ковариации в psi, расчетный параметр дисперсии dispersionи массив ячеек связанной статистики stats. Первая ячейка stats содержит статистику для factory, в то время как вторая ячейка содержит статистику для параметра дисперсии.
Отображение первой ячейки stats чтобы увидеть доверительные интервалы для оценочного параметра ковариации для factory.
stats{1}ans =
Covariance Type: Isotropic
Group Name1 Name2 Type
factory '(Intercept)' '(Intercept)' 'std'
Estimate Lower Upper
0.31381 0.19253 0.51148Колонки Lower и Upper отображение 95% доверительного интервала по умолчанию для расчетного параметра ковариации для factory. Поскольку интервал [0,19253,0,51148] не содержит 0, перехват случайных эффектов значим на уровне значимости 5%. Поэтому, прежде чем делать какие-либо выводы об эффективности нового производственного процесса, необходимо учесть случайный эффект, обусловленный специфическими для завода изменениями.
Сравните модель смешанных эффектов, которая включает перехват случайных эффектов, сгруппированный по factory с моделью, которая не включает случайный эффект, чтобы определить, какая модель лучше подходит для данных. Подогнать первую модель, FEglme, используя только предикторы с фиксированными эффектами newprocess, time_dev, temp_dev, и supplier. Подгонка второй модели, glme, используя эти же предикторы с фиксированными эффектами, но также включая перехват случайных эффектов, сгруппированный по factory.
FEglme = fitglme(mfr,... 'defects ~ 1 + newprocess + time_dev + temp_dev + supplier',... 'Distribution','Poisson','Link','log','FitMethod','Laplace'); glme = fitglme(mfr,... 'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',... 'Distribution','Poisson','Link','log','FitMethod','Laplace');
Сравните две модели, используя тест отношения правдоподобия. Определить 'CheckNesting' как true, так compare возвращает предупреждение, если требования к вложению не удовлетворены.
results = compare(FEglme,glme,'CheckNesting',true)
results =
Theoretical Likelihood Ratio Test
Model DF AIC BIC LogLik LRStat deltaDF
FEglme 6 431.02 446.65 -209.51
glme 7 416.35 434.58 -201.17 16.672 1
pValue
4.4435e-05compare возвращает степени свободы (DF), информационного критерия Акаике (AIC), байесовский информационный критерий (BIC) и регистрировать значения правдоподобия для каждой модели. glme имеет меньшие значения правдоподобия AIC, BIC и log, чем FEglme, что указывает на то, что glme (модель, содержащая термин случайных эффектов для перехвата, сгруппированного по фабрике), является более подходящей моделью для этих данных. Кроме того, небольшое значение p указывает, что compare отвергает нулевую гипотезу о том, что вектор ответа был сгенерирован моделью только с фиксированными эффектами FEglme, в пользу альтернативы, что вектор ответа был сгенерирован моделью смешанных эффектов glme.
Создайте соответствующие условные средние значения для модели.
mufit = fitted(glme);
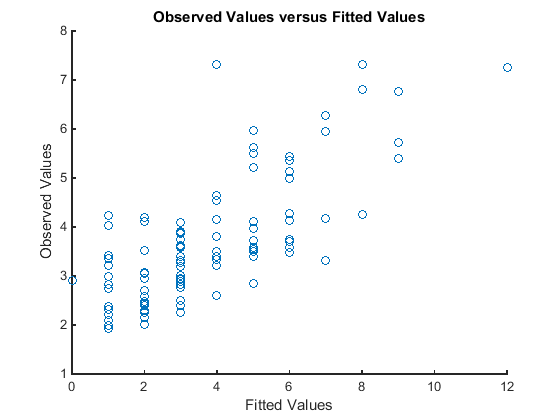
Постройте график между наблюдаемыми значениями отклика и подходящими значениями отклика.
figure scatter(mfr.defects,mufit) title('Observed Values versus Fitted Values') xlabel('Fitted Values') ylabel('Observed Values')
Создание диагностических графиков с использованием условных остатков Пирсона для проверки предположений модели. Поскольку необработанные остатки для обобщенных линейных моделей смешанных эффектов не имеют постоянной дисперсии в наблюдениях, используйте вместо этого условные остатки Пирсона.
Постройте гистограмму, чтобы визуально подтвердить, что среднее значение остатков Пирсона равно 0. Если модель верна, мы ожидаем, что остатки Пирсона будут центрированы в 0.
plotResiduals(glme,'histogram','ResidualType','Pearson')
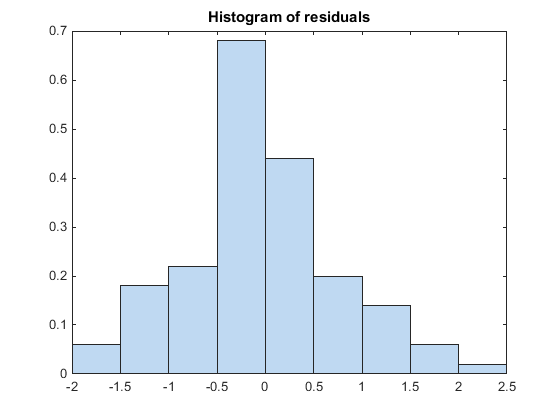
Гистограмма показывает, что остатки Пирсона центрированы в 0.
Постройте график остатков Пирсона по сравнению с подходящими значениями, чтобы проверить признаки непостоянной дисперсии между остатками (гетероскедастичность). Мы ожидаем, что условные остатки Пирсона будут иметь постоянную дисперсию. Следовательно, график условных остатков Пирсона против условных аппроксимированных значений не должен обнаруживать никакой систематической зависимости от условных аппроксимированных значений.
plotResiduals(glme,'fitted','ResidualType','Pearson')
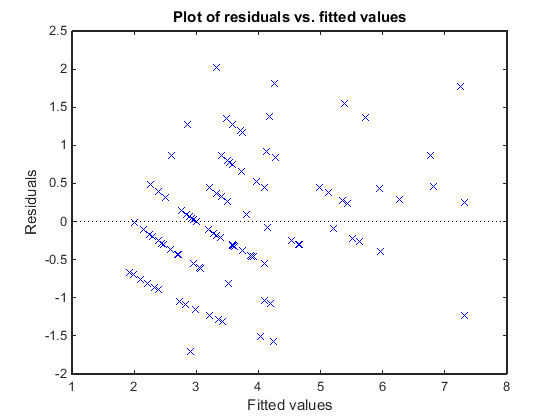
График не показывает систематической зависимости от подогнанных значений, поэтому нет признаков непостоянной дисперсии среди остатков.
Постройте график остатков Пирсона по сравнению с запаздывающими остатками, чтобы проверить корреляцию между остатками. Предположение об условной независимости в GLME подразумевает, что условные остатки Пирсона приблизительно некоррелированы.
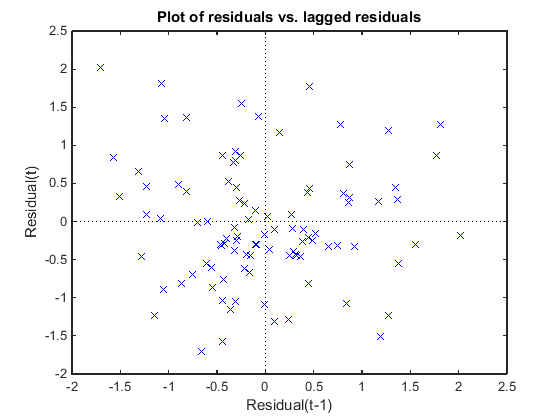
Нет закономерности сюжета, поэтому нет признаков корреляции между остатками.
fitglme | GeneralizedLinearMixedModel