Скрытая модель Маркова (HMM) - это модель, в которой вы наблюдаете последовательность выбросов, но не знаете последовательность состояний, через которые прошла модель для генерации выбросов. Анализ скрытых марковских моделей направлен на восстановление последовательности состояний из наблюдаемых данных.
В качестве примера рассмотрим марковскую модель с двумя состояниями и шестью возможными выбросами. Модель использует:
Красный штамп, имеющий шесть сторон с меткой от 1 до 6.
Зеленая матрица, имеющая двенадцать сторон, пять из которых помечены 2-6, в то время как остальные семь сторон обозначены 1.
Взвешенная красная монета, для которой вероятность головок равна .9, а вероятность хвостов равна .1.
Взвешенная зелёная монета, для которой вероятность головок равна .95, а вероятность хвостов - .05.
Модель создает последовательность чисел из набора {1, 2, 3, 4, 5, 6} со следующими правилами:
Начните с проката красной матрицы и запишите номер, который приходит вверх, который является эмиссией.
Бросьте красную монету и выполните одно из следующих действий:
Если результатом являются головки, катите красный штамп и запишите результат.
Если результатом являются хвосты, сверните зеленый штамп и запишите результат.
На каждом последующем шаге необходимо перевернуть монету, цвет которой совпадает с цветом матрицы, свернутой на предыдущем шаге. Если монета поднимается вверх головками, катите так же, как на предыдущем этапе. Если монета подходит к хвостам, переключитесь на другой штамп.
Диаграмма состояний для этой модели имеет два состояния: красное и зеленое, как показано на следующем рисунке.
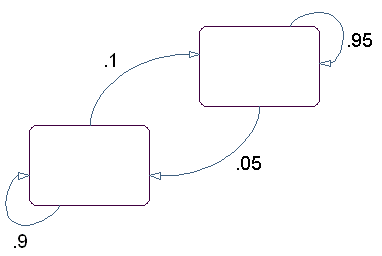
Вы определяете испускание из состояния, катая штамп с тем же цветом, что и состояние. Переход в следующее состояние определяется переворачиванием монеты тем же цветом, что и состояние.
Матрица перехода:
0,90.050.10.95]
Матрица выбросов:
161616161616712112112112112112]
Модель не скрыта, потому что вы знаете последовательность состояний из цветов монет и кости. Предположим, однако, что кто-то другой генерирует выбросы, не показывая вам кости или монеты. Все, что вы видите, это последовательность выбросов. Если вы начнете видеть больше 1, чем другие числа, вы можете заподозрить, что модель находится в зеленом состоянии, но вы не можете быть уверены, потому что вы не видите цвет проката матрицы.
Скрытые марковские модели вызывают следующие вопросы:
Учитывая последовательность выбросов, каков наиболее вероятный путь государства?
С учетом последовательности выбросов как можно оценить вероятность перехода и выбросов модели?
Какова прямая вероятность того, что модель генерирует заданную последовательность?
Какова апостериорная вероятность того, что модель находится в определенном состоянии в любой точке последовательности?
Функции Toolbox™ статистики и машинного обучения, связанные со скрытыми марковскими моделями:
hmmgenerate - Генерирует последовательность состояний и выбросов из марковской модели
hmmestimate - Расчет оценок максимального правдоподобия вероятностей перехода и выбросов из последовательности выбросов и известной последовательности состояний
hmmtrain - рассчитывает оценки максимальной вероятности перехода и вероятности выбросов на основе последовательности выбросов;
hmmviterbi - Вычисляет наиболее вероятный путь к состоянию для скрытой модели Маркова
hmmdecode - Вычисляет вероятности заднего состояния последовательности выбросов
В этом разделе показано, как использовать эти функции для анализа скрытых моделей Маркова.
Следующие команды создают матрицы перехода и излучения для модели, описанной в разделе Введение в скрытые модели Маркова (HMM):
TRANS = [.9 .1; .05 .95]; EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;... 7/12, 1/12, 1/12, 1/12, 1/12, 1/12];
Чтобы создать случайную последовательность состояний и выбросов из модели, используйте hmmgenerate:
[seq,states] = hmmgenerate(1000,TRANS,EMIS);
Продукция seq - последовательность выбросов и выходных данных; states - последовательность состояний.
hmmgenerate начинается в состоянии 1 на шаге 0, переходит в состояние i1 на шаге 1 и возвращает i1 в качестве первой записи в states. Сведения об изменении начального состояния см. в разделе Изменение распределения начального состояния.
С учетом матриц перехода и эмиссии TRANS и EMIS, функция hmmviterbi использует алгоритм Витерби для вычисления наиболее вероятной последовательности состояний, через которые проходит модель для генерации данной последовательности seq выбросов:
likelystates = hmmviterbi(seq, TRANS, EMIS);
likelystates - последовательность той же длины, что и seq.
Проверка точности hmmviterbi, вычислить процент фактической последовательности states что согласуется с последовательностью likelystates.
sum(states==likelystates)/1000 ans = 0.8200
При этом наиболее вероятная последовательность состояний согласуется со случайной последовательностью 82% времени.
Функции hmmestimate и hmmtrain оценка матриц перехода и излучения TRANS и EMIS задана последовательность seq выбросов.
Используя hmmestimate. Функция hmmestimate требует, чтобы вы знали последовательность состояний states что модель прошла через для генерации seq.
Далее берутся последовательности излучения и состояния и возвращаются оценки матриц перехода и излучения:
[TRANS_EST, EMIS_EST] = hmmestimate(seq, states) TRANS_EST = 0.8989 0.1011 0.0585 0.9415 EMIS_EST = 0.1721 0.1721 0.1749 0.1612 0.1803 0.1393 0.5836 0.0741 0.0804 0.0789 0.0726 0.1104
Можно сравнить выходные данные с исходными матрицами перехода и излучения, TRANS и EMIS:
TRANS TRANS = 0.9000 0.1000 0.0500 0.9500 EMIS EMIS = 0.1667 0.1667 0.1667 0.1667 0.1667 0.1667 0.5833 0.0833 0.0833 0.0833 0.0833 0.0833
Используя hmmtrain. Если последовательность состояний неизвестна states, но у вас есть начальные догадки для TRANS и EMIS, вы все еще можете оценить TRANS и EMIS использование hmmtrain.
Предположим, что у вас есть следующие начальные догадки для TRANS и EMIS.
TRANS_GUESS = [.85 .15; .1 .9]; EMIS_GUESS = [.17 .16 .17 .16 .17 .17;.6 .08 .08 .08 .08 08];
Вы оцениваете TRANS и EMIS следующим образом:
[TRANS_EST2, EMIS_EST2] = hmmtrain(seq, TRANS_GUESS, EMIS_GUESS) TRANS_EST2 = 0.2286 0.7714 0.0032 0.9968 EMIS_EST2 = 0.1436 0.2348 0.1837 0.1963 0.2350 0.0066 0.4355 0.1089 0.1144 0.1082 0.1109 0.1220
hmmtrain использует итеративный алгоритм, изменяющий матрицы TRANS_GUESS и EMIS_GUESS чтобы на каждом этапе скорректированные матрицы с большей вероятностью генерировали наблюдаемую последовательность, seq. Алгоритм останавливается, когда матрицы в двух последовательных итерациях находятся в пределах небольшого допуска друг от друга.
Если алгоритму не удается достичь этого допуска в пределах максимального числа итераций, значением по умолчанию которого является 100алгоритм останавливается. В этом случае hmmtrain возвращает последние значения TRANS_EST и EMIS_EST и предупреждает о том, что допуск не достигнут.
Если алгоритм не достигает требуемого допуска, увеличьте значение по умолчанию максимального числа итераций с помощью команды:
hmmtrain(seq,TRANS_GUESS,EMIS_GUESS,'maxiterations',maxiter)
где maxiter - максимальное количество шагов, выполняемых алгоритмом.
Измените значение допуска по умолчанию с помощью команды:
hmmtrain(seq, TRANS_GUESS, EMIS_GUESS, 'tolerance', tol)
где tol - требуемое значение допуска. Увеличение значения tol заставляет алгоритм остановиться раньше, но результаты менее точны.
Два фактора снижают надежность выходных матриц hmmtrain:
Алгоритм сходится к локальному максимуму, который не представляет истинные матрицы перехода и излучения. Если вы подозреваете это, используйте различные начальные догадки для матриц TRANS_EST и EMIS_EST.
Последовательность seq может быть слишком коротким, чтобы правильно обучить матрицы. Если вы подозреваете это, используйте более длинную последовательность для seq.
Вероятности заднего состояния последовательности эмиссии seq - условные вероятности того, что модель находится в определенном состоянии, когда она генерирует символ в seq, учитывая, что seq испускается. Вы вычисляете вероятности заднего состояния с помощью hmmdecode:
PSTATES = hmmdecode(seq,TRANS,EMIS)
Продукция PSTATES - матрица M-by-L, где M - число состояний, а L - длина seq. PSTATES(i,j) - условная вероятность того, что модель находится в состоянии i когда он генерирует j-й символ seq, учитывая, что seq испускается.
hmmdecode начинается с модели в состоянии 1 на шаге 0, перед первым излучением. PSTATES(i,1) - вероятность того, что модель находится в состоянии i на следующем шаге 1. Сведения об изменении начального состояния см. в разделе Изменение распределения начального состояния.
Возврат логарифма вероятности последовательности seq, используйте второй выходной аргумент hmmdecode:
[PSTATES,logpseq] = hmmdecode(seq,TRANS,EMIS)
Вероятность последовательности стремится к 0 по мере увеличения длины последовательности, и вероятность достаточно длинной последовательности становится меньше, чем наименьшее положительное число, которое может представить компьютер. hmmdecode возвращает логарифм вероятности избежать этой проблемы.
По умолчанию в состоянии 1 начинаются скрытые функции модели Маркова (Statistics and Machine Learning Toolbox). Другими словами, распределение начальных состояний имеет всю свою вероятностную массу, сконцентрированную в состоянии 1. Для назначения другого распределения вероятностей p = [p1, p2,..., pM] M начальным состояниям выполните следующее:
Создайте дополненного перехода M + 1 по M + 1, T ^ следующего вида:
0p0T]
где T - истинная матрица перехода. Первый столбец ^ содержит M + 1 нулей. p должен быть равен 1.
Создайте дополненную матрицу эмиссии M + 1-by-N, E ^, которая имеет следующий вид:
0E]
Если матрицы перехода и излучения TRANS и EMIS, соответственно, можно создать дополненные матрицы с помощью следующих команд.
TRANS_HAT = [0 p; zeros(size(TRANS,1),1) TRANS]; EMIS_HAT = [zeros(1,size(EMIS,2)); EMIS];
hmmdecode | hmmestimate | hmmgenerate | hmmtrain | hmmviterbi