Неклассическое многомерное масштабирование
Y = mdscale(D,p)
[Y,stress] = mdscale(D,p)
[Y,stress,disparities] = mdscale(D,p)
[...] = mdscale(D,p,'Name',value)
Y = mdscale(D,p) выполняет неметрическое многомерное масштабирование матрицы n-на-n разнородности D, и возвращает Y, конфигурация n точек (строк) в p размеры (колонны). Евклидовы расстояния между точками в Y аппроксимировать монотонное преобразование соответствующих разнородностей в D. По умолчанию mdscale использует нормированный критерий стресс1 Крускала.
Можно указать D либо в виде полной матрицы n-на-n, либо в форме верхнего треугольника, например, выводимой pdist. Матрица полной разнородности должна быть действительной и симметричной и иметь нули вдоль диагональных и неотрицательных элементов везде. Матрица разнородности в форме верхнего треугольника должна иметь вещественные неотрицательные записи. mdscale удовольствия NaNs в D как отсутствующие значения и игнорирует эти элементы. Inf не принимается.
Можно также указать D в качестве полной матрицы подобия, с элементами по диагонали и всеми другими элементами меньше единицы. mdscale преобразует матрицу подобия в матрицу различия таким образом, что расстояния между точками, возвращенными в Y приблизительный sqrt(1-D). Чтобы использовать другое преобразование, преобразуйте подобия перед вызовом mdscale.
[Y,stress] = mdscale(D,p) возвращает минимизированное напряжение, т.е. напряжение, вычисленное в Y.
[Y,stress,disparities] = mdscale(D,p) возвращает различия, то есть монотонное преобразование различий D.
[...] = mdscale(D,p,' указывает одну или несколько необязательных пар имя/значение параметра, которые управляют дополнительными подробностями Name',value)mdscale. Определить Name в одиночных кавычках. Доступные параметры:
Criterion- Критерий пригодности для минимизации. Это также определяет тип масштабирования, неметрическое или метрическое, который mdscale выполняет. Варианты неметрического масштабирования:
'stress' - Напряжение, нормализованное по сумме квадратов межточечных расстояний, также известное как напряжение1. Это значение по умолчанию.
'sstress' - напряжение в квадрате, нормированное с суммой 4-х степеней межточечных расстояний.
Варианты масштабирования метрики:
'metricstress' - Напряжение, нормированное с суммой квадратов различий.
'metricsstress' - Напряжение в квадрате, нормированное с суммой 4-х степеней различий.
'sammon' - критерий нелинейного отображения Саммона. Недиагональные различия должны быть строго положительными с этим критерием.
'strain' - критерий, эквивалентный критерию, используемому при классическом многомерном масштабировании.
Weights - матрица или вектор того же размера, что и D, содержащий неотрицательные весы несходимости. Их можно использовать для взвешивания вклада соответствующих элементов D в вычислениях и минимизации напряжения. Элементы D соответствующие нулевым весам фактически игнорируются.
Примечание
При указании весов как полной матрицы ее диагональные элементы игнорируются и не имеют эффекта, так как соответствующие диагональные элементы D не вводите в расчет напряжения.
Start - Метод, используемый для выбора начальной конфигурации точек для Y. Варианты:
'cmdscale' - использование классического решения многомерного масштабирования. Это значение по умолчанию. 'cmdscale' недопустим при нулевых весах.
'random' - Выбирайте местоположения случайным образом из соответствующего масштабированного p-мерного нормального распределения с некоррелированными координатами.
N-by-p матрица начальных расположений, где n - размер матрицы D и p - количество столбцов выходной матрицы Y. В этом случае можно пройти [] для p и mdscale выводит p от второго размера матрицы. Можно также предоставить массив 3-D, подразумевая значение для 'Replicates' из третьего измерения массива.
Replicates - количество повторений масштабирования с новой начальной конфигурацией. Значение по умолчанию: 1.
Options - опции итеративного алгоритма, используемого для минимизации критерия подгонки. Передача структуры опций, созданной statset. Например,
opts = statset(param1,val1,param2,val2, ...); [...] = mdscale(...,'Options',opts)
Выбор statset параметры:
'Display' - уровень вывода на дисплей. Выбор: 'off' (по умолчанию), 'iter', и 'final'.
'MaxIter' - максимально допустимое число итераций. Значение по умолчанию: 200.
'TolFun' - Допуск окончания для критерия напряжения и его градиента. Значение по умолчанию: 1e-4.
'TolX'- Допуск окончания для размера шага расположения конфигурации. Значение по умолчанию: 1e-4.
load cereal.mat
X = [Calories Protein Fat Sodium Fiber ...
Carbo Sugars Shelf Potass Vitamins];
% Take a subset from a single manufacturer.
X = X(strcmp('K',cellstr(Mfg)),:);
% Create a dissimilarity matrix.
dissimilarities = pdist(X);
% Use non-metric scaling to recreate the data in 2D,
% and make a Shepard plot of the results.
[Y,stress,disparities] = mdscale(dissimilarities,2);
distances = pdist(Y);
[dum,ord] = sortrows([disparities(:) dissimilarities(:)]);
plot(dissimilarities,distances,'bo', ...
dissimilarities(ord),disparities(ord),'r.-');
xlabel('Dissimilarities'); ylabel('Distances/Disparities')
legend({'Distances' 'Disparities'},'Location','NW');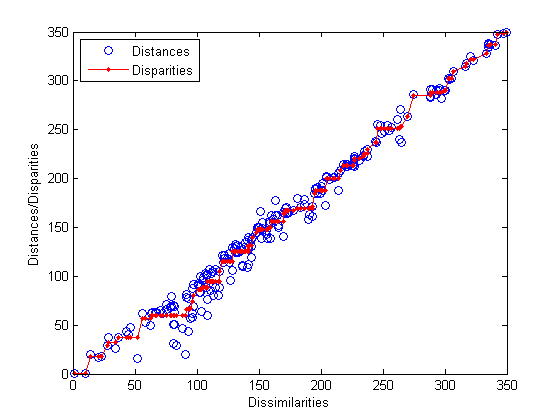
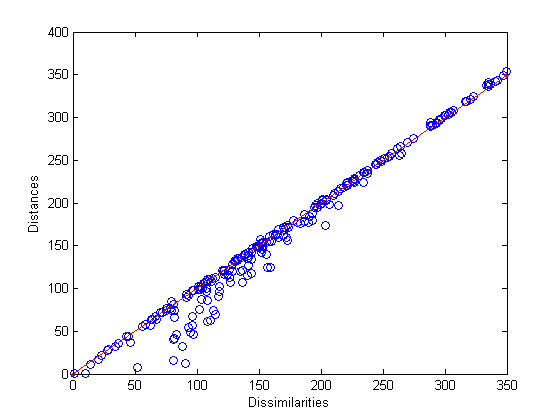
% Do metric scaling on the same dissimilarities.
figure
[Y,stress] = ...
mdscale(dissimilarities,2,'criterion','metricsstress');
distances = pdist(Y);
plot(dissimilarities,distances,'bo', ...
[0 max(dissimilarities)],[0 max(dissimilarities)],'r.-');
xlabel('Dissimilarities'); ylabel('Distances')