В статистике эффект - это все, что влияет на значение переменной ответа при конкретной установке переменных предиктора. Эффекты преобразуются в параметры модели. В линейных моделях эффекты становятся коэффициентами, представляющими пропорциональные вклады модельных членов. В нелинейных моделях эффекты часто имеют специфические физические интерпретации и появляются в более общих нелинейных комбинациях.
Фиксированные эффекты представляют параметры совокупности, предполагаемые одинаковыми при каждом сборе данных. Оценка фиксированных эффектов является традиционной областью регрессионного моделирования. Случайные эффекты, для сравнения, являются случайными переменными, зависящими от выборки. В моделировании случайные эффекты действуют как дополнительные члены ошибки, и их распределения и ковариации должны быть определены.
Например, рассмотрим модель выведения препарата из кровотока. Модель использует время t в качестве предиктора и концентрацию лекарства С в качестве ответа. Термин нелинейной модели C0e-rt объединяет параметры C0 и r, представляющие, соответственно, начальную концентрацию и скорость исключения. Если данные собираются по нескольким индивидуумам, разумно предположить, что скорость исключения является случайной переменной ri в зависимости от индивидуума i, варьирующейся вокруг среднего значения популяции. Термин C0e-rt становится
C0e − (β + bi) t,
где β = - фиксированный эффект, а bi = r - случайный эффект.
Случайные эффекты полезны, когда данные попадают в естественные группы. В модели элиминации лекарств группы являются просто исследуемыми лицами. Более сложные модели могут группировать данные по возрасту, весу, диете и т. Д. Хотя группы не являются фокусом исследования, добавление случайных эффектов к модели расширяет надежность выводов за пределы конкретной выборки людей.
Модели смешанных эффектов учитывают как фиксированные, так и случайные эффекты. Как и во всех регрессионных моделях, их целью является описание переменной ответа как функции переменных предиктора. Модели со смешанными эффектами, однако, распознают корреляции в подгруппах образцов. Таким образом, они обеспечивают компромисс между полным игнорированием групп данных и подгонкой каждой группы с помощью отдельной модели.
Предположим, что данные для модели нелинейной регрессии попадают в одну из m различных групп i = 1,..., m. Чтобы учесть группы в модели, запишите ответ j в группу i как:
+ αij
yij - ответная реакция, xij - вектор предикторов, start- вектор параметров модели, αij - погрешность измерения или процесса. Индекс j находится в диапазоне от 1 до ni, где ni - количество наблюдений в группе i. Функция f определяет форму модели. Часто xij - это просто время наблюдения tij. Ошибки обычно считаются независимыми и идентичными, обычно распределенными с постоянной дисперсией.
Оценки параметров в startописывают популяцию, предполагая, что эти оценки одинаковы для всех групп. Если, однако, оценки различаются по группам, модель становится
+ αij
В модели со смешанными эффектами γ i может быть комбинацией фиксированного и случайного эффекта:
+ bi
Случайные эффекты bi обычно описываются как многомерные, нормально распределенные, со средним нулем и ковариацией ("covariance Оценивая фиксированные эффекты β и ковариацию случайных эффектов ("" convariance of the random effects ""), дает описание совокупности, которая не предполагает, что параметры "" "" "" "" "" "" "" "" "" "" "" "" "" "" "" "" " Оценка случайных эффектов bi также дает описание конкретных групп в данных.
Параметры модели не должны идентифицироваться с помощью отдельных эффектов. В общем случае для идентификации параметров с линейными комбинациями фиксированных и случайных эффектов используются расчетные матрицы А и В:
Bbi
Если матрицы конструкции различаются между группами, модель становится
Биби
Если матрицы конструкции также различаются между наблюдениями, модель становится
xij) + αij
Некоторые из групповых предикторов в xij могут не меняться при наблюдении j. Назвав эти vi, модель становится
) + αij
Предположим, что данные для модели нелинейной регрессии попадают в одну из m различных групп i = 1,..., m. (В частности, предположим, что группы не вложены.) Чтобы задать общую нелинейную модель смешанных эффектов для этих данных:
Определите параметры модели, специфичные для группы, как линейные комбинации фиксированных эффектов β и случайных эффектов bi.
Определите значения ответа yi как нелинейную функцию f параметров и специфичных для группы предикторных переменных Xi.
Модель:
εi∼N (0, start2)
Эта формулировка нелинейной модели смешанных эффектов использует следующую нотацию:
| φi | Вектор параметров модели, специфичных для группы |
| β | Вектор фиксированных эффектов, моделирование параметров заполнения |
| bi | Вектор многомерных нормально распределенных групповых случайных эффектов |
| Ай | Матрица проектирования для конкретных групп для комбинирования фиксированных эффектов |
| Висмут | Матрица проектирования для конкретных групп для комбинирования случайных эффектов |
| Си | Матрица данных значений предиктора для конкретной группы |
| yi | Вектор данных значений ответа для конкретной группы |
| f | Общая, вещественно-значимая функция для objecti и Xi |
| εi | Вектор специфичных для группы ошибок, предполагаемый как независимый, идентичный, нормально распределенный и независимый от bi |
| Ψ | Ковариационная матрица для случайных эффектов |
| σ2 | Дисперсия ошибок, предполагаемая постоянной для всех наблюдений |
Например, рассмотрим модель выведения препарата из кровотока. Модель включает две перекрывающиеся фазы:
Начальная фаза p, в течение которой концентрации лекарств достигают равновесия с окружающими тканями
Вторая фаза q, во время которой лекарственное средство удаляется из кровотока
Для данных о нескольких лицах i модель
rqitij + αij,
где yij - наблюдаемая концентрация в индивидууме i во время tij. Модель допускает различное время выборки и различное количество наблюдений для разных людей.
Скорости исключения rpi и rqi должны быть положительными, чтобы быть физически значимыми. Обеспечьте это путем введения логарифмических скоростей Rpi = log (rpi) и Rqi = log (rqi) и репарамеризации модели:
Rqi) tij + αij
Выбор параметров для моделирования со случайными эффектами является важным фактором при построении модели со смешанными эффектами. Один из методов заключается в добавлении случайных эффектов ко всем параметрам и использовании оценок их дисперсий для определения их значимости в модели. Альтернативой является подгонка модели отдельно к каждой группе без случайных эффектов и просмотр вариаций оценок параметров. Если оценка сильно варьируется по группам или если доверительные интервалы для каждой группы имеют минимальное перекрытие, параметр является хорошим кандидатом для случайного эффекта.
Чтобы ввести фиксированные эффекты β и случайные эффекты bi для всех параметров модели, повторно экспрессируйте модель следующим образом:
+ b1i) e − ex
В нотации общей модели:
(ti1⋮tini),
где ni - количество наблюдений отдельных i. В этом случае матрицы Ai и Bi проектирования являются, по крайней мере изначально, матрицами тождества 4 на 4. Матрицы проектирования могут быть изменены, при необходимости, для введения взвешивания отдельных эффектов или зависимости от времени.
Подгонка модели и оценка ковариационной матрицы Startчасто приводит к дальнейшим уточнениям. Относительно небольшая оценка дисперсии случайного эффекта предполагает, что его можно удалить из модели. Аналогично, относительно небольшие оценки ковариаций среди определенных случайных эффектов предполагают, что полная ковариационная матрица не нужна. Так как случайные эффекты не наблюдаются, Ψ должен быть оценен косвенно. Задание диагональной или блочно-диагональной ковариационной схемы для, может улучшить сходимость и эффективность алгоритма аппроксимации.
Функции Toolbox™ статистики и машинного обучения nlmefit и nlmefitsa подгонять общую нелинейную модель смешанных эффектов к данным, оценивая фиксированные и случайные эффекты. Функции также оценивают ковариационную матрицу для случайных эффектов. Дополнительные диагностические результаты позволяют оценить компромиссы между количеством параметров модели и степенью соответствия.
Если модель в разделе Определение моделей смешанных эффектов предполагает зависимую от группы ковариату, такую как вес (w), модель становится:
Таким образом, параметр фi для любого индивидуума в iВ-ю группу входят:
Чтобы указать ковариатную модель, используйте 'FEGroupDesign' вариант.
'FEGroupDesign' является p-by-q-by-m массив, указывающий другое p-by-q матрица проектирования с фиксированными эффектами для каждого из m группы. В предыдущем примере массив напоминает следующий:
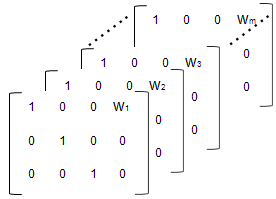
Создайте массив.
% Number of parameters in the model (Phi) num_params = 3; % Number of covariates num_cov = 1; % Assuming number of groups in the data set is 7 num_groups = 7; % Array of covariate values covariates = [75; 52; 66; 55; 70; 58; 62 ]; A = repmat(eye(num_params, num_params+num_cov),... [1,1,num_groups]); A(1,num_params+1,1:num_groups) = covariates(:,1)
Создать struct с указанной конструктивной матрицей.
options.FEGroupDesign = A;
Укажите аргументы для nlmefit (или nlmefitsa), как показано в моделях смешанных эффектов с использованием nlmefit и nlmefita.
nlmefit или nlmefitsaНабор инструментов для статистики и машинного обучения предоставляет две функции: nlmefit и nlmefitsa для подгонки нелинейных моделей смешанных эффектов. Каждая функция предоставляет различные возможности, которые могут помочь вам решить, какие из них использовать.
nlmefit предоставляет следующие четыре метода аппроксимации для подгонки нелинейных моделей смешанных эффектов:
'LME' - Использовать вероятность для линейной модели смешанных эффектов при текущих условных оценках beta и B. Это значение по умолчанию.
'RELME' - Использовать ограниченную вероятность для линейной модели смешанных эффектов при текущих условных оценках beta и B.
'FO' - лапласовое приближение первого порядка без случайных эффектов.
'FOCE' - Лапласианское приближение первого порядка при условных оценках B.
nlmefitsa предоставляет дополнительный метод аппроксимации, стохастическое аппроксимационное ожидание-максимизация (SAEM) [25] с тремя шагами:
Моделирование: Генерировать смоделированные значения случайных эффектов b из задней плотности p (b 'Λ), учитывая текущие оценки параметров.
Стохастическая аппроксимация: Обновите ожидаемое значение функции логарифмического правдоподобия, взяв его значение из предыдущего шага и переместив часть пути к среднему значению логарифмического правдоподобия, вычисленному из моделируемых случайных эффектов.
Шаг максимизации: Выберите новые оценки параметров, чтобы максимизировать логарифмическую функцию правдоподобия, учитывая смоделированные значения случайных эффектов.
Оба nlmefit и nlmefitsa попытка найти оценки параметров для максимизации функции правдоподобия, которую трудно вычислить. nlmefit имеет дело с проблемой, аппроксимируя функцию правдоподобия различными способами и максимизируя аппроксимированную функцию. В ней используются традиционные методы оптимизации, зависящие от таких факторов, как критерии сходимости и пределы итерации.
nlmefitsaс другой стороны, моделирует случайные значения параметров таким образом, что в долгосрочной перспективе они сходятся к значениям, которые максимизируют точную функцию правдоподобия. Результаты случайны, и традиционные тесты сходимости не применяются. Поэтому nlmefitsa предоставляет опции для печати результатов по мере выполнения моделирования и многократного перезапуска моделирования. Эти функции можно использовать для определения того, были ли результаты сходятся с желаемой точностью.
nlmefitsaСледующие параметры специфичны для nlmefitsa. Большинство из них управляют стохастическим алгоритмом.
Cov0 - Начальное значение ковариационной матрицы PSI. Должна быть r-by-r положительной определенной матрицей. Если пусто, значение по умолчанию зависит от значений BETA0.
ComputeStdErrors — true для вычисления стандартных ошибок для оценок коэффициентов и сохранения их в выходных данных STATS структура, или false (по умолчанию), чтобы опустить это вычисление.
LogLikMethod - задает метод аппроксимации логарифмического правдоподобия.
NBurnIn - количество начальных итераций записи, в течение которых оценки параметров не пересчитываются. Значение по умолчанию - 5.
NIterations - управляет количеством итераций, выполняемых для каждой из трех фаз алгоритма.
NMCMCIterations - Количество итераций цепи Маркова Монте-Карло (MCMC).
Есть некоторые различия в возможностях nlmefit и nlmefitsa. Поэтому некоторые данные и модели можно использовать с любой из функций, но некоторые могут потребовать выбора только одной из них.
Модели ошибок - nlmefitsa поддерживает различные модели ошибок. Например, стандартное отклонение отклика может быть постоянным, пропорциональным значению функции или комбинации этих двух значений. nlmefit подходит для моделей в предположении, что стандартное отклонение отклика является постоянным. Одна из моделей ошибок, 'exponential'указывает, что журнал ответа имеет постоянное стандартное отклонение. Подогнать такие модели можно с помощью nlmefit путем предоставления логарифмического ответа в качестве входных данных и путем перезаписи функции модели для получения логарифмического значения нелинейной функции.
Случайные эффекты - обе функции подгоняют данные к нелинейной функции с параметрами, и параметры могут быть простыми скалярными значениями или линейными функциями ковариат. nlmefit позволяет любым коэффициентам линейных функций иметь как фиксированные, так и случайные эффекты. nlmefitsa поддерживает случайные эффекты только для постоянного (коэффициента пересечения) линейных функций, но не для коэффициентов наклона. Итак, в примере «Определение ковариатных моделей» nlmefitsa может рассматривать только первые три бета-значения как случайные эффекты.
Форма модели - nlmefit поддерживает очень общую спецификацию модели с несколькими ограничениями на матрицы конструкции, которые связывают фиксированные коэффициенты и случайные эффекты с параметрами модели. nlmefitsa является более ограничительным:
Конструкция с фиксированным эффектом должна быть постоянной в каждой группе (для каждого индивидуума), поэтому конструкция, зависящая от наблюдения, не поддерживается.
Конструкция случайного эффекта должна быть постоянной для всего набора данных, поэтому не поддерживается ни конструкция, зависящая от наблюдения, ни конструкция, зависящая от группы.
Как упомянуто в разделе Случайные эффекты, конструкция случайного эффекта не должна задавать случайные эффекты для коэффициентов наклона. Это означает, что конструкция должна состоять из нулей и единиц.
Конструкция случайного эффекта не должна использовать один и тот же случайный эффект для нескольких коэффициентов и не может использовать более одного случайного эффекта для одного коэффициента.
Конструкция с фиксированным эффектом не должна использовать один и тот же коэффициент для нескольких параметров. Это означает, что он может иметь не более одного ненулевого значения в каждом столбце.
Если вы хотите использовать nlmefitsa для данных, в которых ковариатные эффекты являются случайными, включить ковариаты непосредственно в выражение нелинейной модели. Не включайте ковариаты в матрицы конструкции с фиксированным или случайным эффектом.
Сходимость - как описано в форме Модель, nlmefit и nlmefitsa имеют различные подходы к измерению сходимости. nlmefit использует традиционные меры оптимизации, и nlmefitsa обеспечивает диагностику, помогающую судить о сходимости случайного моделирования.
На практике, nlmefitsa как правило, они являются более надежными и менее склонны к сбоям в решении сложных проблем. Однако nlmefit может быстрее сойтись по проблемам, где вообще сойдётся. Некоторые проблемы могут выиграть от комбинированной стратегии, например, запуск nlmefitsa на некоторое время для получения разумных оценок параметров и использования их в качестве отправной точки для дополнительных итераций с использованием nlmefit.
Outputfcn области options структура определяет одну или несколько функций, вызываемых решателем после каждой итерации. Как правило, функция вывода может использоваться для построения точек в каждой итерации или для отображения величин оптимизации из алгоритма. Чтобы настроить функцию вывода:
Запишите функцию вывода как файловую функцию MATLAB ® или локальную функцию.
Использовать statset для установки значения Outputfcn быть дескриптором функции, то есть именем функции, которой предшествует @ знак. Например, если функция вывода outfun.m, команда
options = statset('OutputFcn', @outfun);определяет OutputFcn быть дескриптором для outfun. Чтобы указать несколько функций вывода, используйте синтаксис:
options = statset('OutputFcn',{@outfun, @outfun2});Вызовите функцию оптимизации с помощью options в качестве входного аргумента.
Пример функции вывода см. в разделе Выборка функции вывода.
Строка определения функции вывода имеет следующий вид:
stop = outfun(beta,status,state)
бета - текущие фиксированные эффекты.
- это структура, содержащая данные текущей итерации. Поля со статусом подробно описывают структуру.
state - текущее состояние алгоритма. Состояния алгоритма перечисляют возможные значения.
stop - флаг, который true или false в зависимости от того, должна ли процедура оптимизации завершаться или продолжаться. Дополнительные сведения см. в разделе Флаг остановки.
Решатель передает значения входных аргументов в outfun на каждой итерации.
В следующей таблице перечислены поля status структура:
| Область | Описание |
|---|---|
procedure |
|
iteration | Целое число, начинающееся от 0. |
inner |
Структура, описывающая статус внутренних итераций в пределах
|
fval | Текущее правдоподобие журнала |
Psi | Текущая ковариационная матрица случайных эффектов |
theta | Текущая параметризация Psi |
mse | Текущее отклонение ошибки |
В следующей таблице перечислены возможные значения для state:
| государство | Описание |
|---|---|
| Алгоритм находится в начальном состоянии перед первой итерацией. |
| Алгоритм находится в конце итерации. |
| Алгоритм находится в конечном состоянии после последней итерации. |
Следующий код иллюстрирует, как функция вывода может использовать значение state чтобы решить, какие задачи выполнять в текущей итерации:
switch state
case 'iter'
% Make updates to plot or guis as needed
case 'init'
% Setup for plots or guis
case 'done'
% Cleanup of plots, guis, or final plot
otherwise
endВыходной аргумент stop является флагом, который true или false. Флаг указывает решателю, следует ли ему выйти или продолжить работу. Следующие примеры показывают типичные способы использования stop флаг.
Остановка оптимизации на основе промежуточных результатов. Функция вывода может остановить оценку в любой итерации на основе значений аргументов, переданных в нее. Например, следующий код устанавливает значение stop равным true на основе значения правдоподобия журнала, сохраненного в 'fval'поле структуры статуса:
stop = outfun(beta,status,state)
stop = false;
% Check if loglikelihood is more than 132.
if status.fval > -132
stop = true;
endОстановка итерации на основе ввода графического интерфейса пользователя. При проектировании графического интерфейса пользователя для выполнения nlmefit итерации можно остановить функцию вывода, когда пользователь нажимает кнопку Остановить (Stop) в графическом интерфейсе пользователя. Например, следующий код реализует диалог для отмены вычислений:
function retval = stop_outfcn(beta,str,status)
persistent h stop;
if isequal(str.inner.state,'none')
switch(status)
case 'init'
% Initialize dialog
stop = false;
h = msgbox('Press STOP to cancel calculations.',...
'NLMEFIT: Iteration 0 ');
button = findobj(h,'type','uicontrol');
set(button,'String','STOP','Callback',@stopper)
pos = get(h,'Position');
pos(3) = 1.1 * pos(3);
set(h,'Position',pos)
drawnow
case 'iter'
% Display iteration number in the dialog title
set(h,'Name',sprintf('NLMEFIT: Iteration %d',...
str.iteration))
drawnow;
case 'done'
% Delete dialog
delete(h);
end
end
if stop
% Stop if the dialog button has been pressed
delete(h)
end
retval = stop;
function stopper(varargin)
% Set flag to stop when button is pressed
stop = true;
disp('Calculation stopped.')
end
end
nmlefitoutputfcn - образец выходной функции панели инструментов статистики и машинного обучения для nlmefit и nlmefitsa. Он инициализирует или обновляет график с фиксированными эффектами (BETA) и дисперсия случайных эффектов (diag(STATUS.Psi)). Для nlmefit, сюжет также включает логарифмическое правдоподобие (STATUS.fval).
nlmefitoutputfcn является функцией вывода по умолчанию для nlmefitsa. Чтобы использовать его с nlmefit, укажите дескриптор функции для него в структуре опций:
opt = statset('OutputFcn', @nlmefitoutputfcn, …)
beta = nlmefit(…, 'Options', opt, …)nlmefitsa из использования этой функции укажите пустое значение для выходной функции:opt = statset('OutputFcn', [], …)
beta = nlmefitsa(…, 'Options', opt, …)nlmefitoutputfcn остановки nlmefit или nlmefitsa при закрытии создаваемой фигуры.