Выполнение неклассического многомерного масштабирования с помощью mdscale.
Функция mdscale выполняет неклассическое многомерное масштабирование. Как и с cmdscale, вы используете mdscale либо визуализировать разнородные данные, для которых не существует «местоположений», либо визуализировать высокоразмерные данные путем уменьшения их размерности. Обе функции принимают матрицу разнородностей в качестве входных данных и создают конфигурацию точек. Однако mdscale предлагает выбор различных критериев для построения конфигурации и допускает отсутствие данных и весов.
Например, данные по зерновым включают измерения по 10 переменным, описывающим хлопья для завтрака. Вы можете использовать mdscale для визуализации этих данных в двух измерениях. Сначала загрузите данные. Для ясности этот пример кода выбирает подмножество из 22 наблюдений.
load cereal.mat
X = [Calories Protein Fat Sodium Fiber ...
Carbo Sugars Shelf Potass Vitamins];
% Take a subset from a single manufacturer
mfg1 = strcmp('G',cellstr(Mfg));
X = X(mfg1,:);
size(X)
ans =
22 10Затем использовать pdist преобразование 10-мерных данных в разнородности. Выходные данные pdist - симметричная матрица разнородности, хранящаяся в виде вектора, содержащего только элементы (23 * 22/2) в его верхнем треугольнике.
dissimilarities = pdist(zscore(X),'cityblock');
size(dissimilarities)
ans =
1 231Этот пример кода сначала стандартизирует данные зерновых, а затем использует расстояние городского блока в качестве отличия. Выбор преобразования в разнородность зависит от приложения, и выбор здесь только для простоты. В некоторых приложениях исходные данные уже имеют форму разнородностей.
Далее используйте mdscale для выполнения метрической MDS. В отличие от этого, cmdscale, необходимо указать требуемое количество размеров и метод, используемый для создания выходной конфигурации. В этом примере используются два размера. Метрический критерий STRESS является общим методом вычисления выходного сигнала; для получения информации о других вариантах см. mdscale справочная страница в онлайн-документации. Второй выход из mdscale - значение этого критерия, вычисленное для выходной конфигурации. Он измеряет, насколько хорошо межточечные расстояния выходной конфигурации приближаются к исходным входным различиям:
[Y,stress] =...
mdscale(dissimilarities,2,'criterion','metricstress');
stress
stress =
0.1856Разброс выходных данных mdscale представляет исходные 10-мерные данные в двух измерениях, и можно использовать gname для маркировки выбранных точек:
plot(Y(:,1),Y(:,2),'o','LineWidth',2); gname(Name(mfg1))
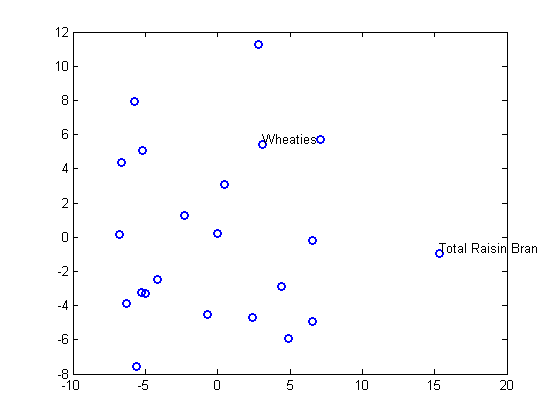
Метрическое многомерное масштабирование создает конфигурацию точек, межточечные расстояния которых аппроксимируют заданные различия. Это иногда слишком строгое требование, и неметрическое масштабирование разработано, чтобы немного расслабить его. Вместо того, чтобы пытаться аппроксимировать сами разнородности, неметрическое масштабирование аппроксимирует нелинейное, но монотонное их преобразование. Из-за монотонности большие или меньшие расстояния на графике выходного сигнала будут соответствовать большим или меньшим различиям, соответственно. Однако нелинейность подразумевает, что mdscale только попытки сохранить упорядоченность разнородностей. Таким образом, могут иметь место сокращения или расширения расстояний в различных масштабах.
Вы используете mdscale для выполнения неметрической MDS во многом так же, как для метрического масштабирования. Неметрический критерий СТРЕСС является обычным методом вычисления выходного сигнала; для получения дополнительной информации см. mdscale справочная страница в онлайн-документации. Как и при метрическом масштабировании, второй выход из mdscale - значение этого критерия, вычисленное для выходной конфигурации. Для неметрического масштабирования, однако, он измеряет, насколько хорошо межточечные расстояния выходной конфигурации аппроксимируют различия. Различия возвращаются в третьем выпуске. Они являются преобразованными значениями исходных различий:
[Y,stress,disparities] = ...
mdscale(dissimilarities,2,'criterion','stress');
stress
stress =
0.1562Чтобы проверить соответствие выходной конфигурации различиям и понять различия, это помогает сделать график Шепарда:
distances = pdist(Y);
[dum,ord] = sortrows([disparities(:) dissimilarities(:)]);
plot(dissimilarities,distances,'bo', ...
dissimilarities(ord),disparities(ord),'r.-', ...
[0 25],[0 25],'k-')
xlabel('Dissimilarities')
ylabel('Distances/Disparities')
legend({'Distances' 'Disparities' '1:1 Line'},...
'Location','NorthWest');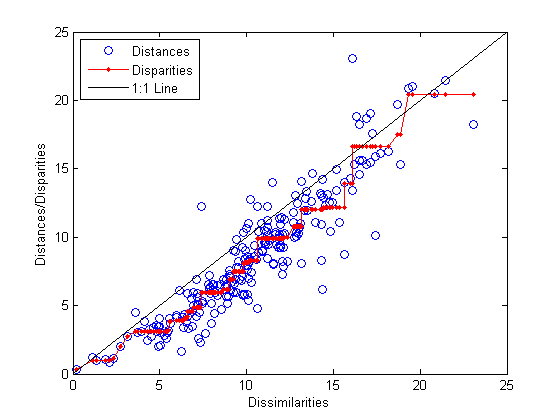
Этот сюжет показывает, что mdscale обнаружил конфигурацию точек в двух измерениях, межточечные расстояния которых аппроксимируют различия, которые, в свою очередь, являются нелинейным преобразованием исходных разнородностей. Вогнутая форма различий как функция различий указывает на то, что подгонка имеет тенденцию сокращать небольшие расстояния относительно соответствующих различий. Это может быть вполне приемлемым на практике.
mdscale использует итеративный алгоритм для поиска выходной конфигурации, и результаты часто могут зависеть от начальной точки. По умолчанию mdscale использование cmdscale для построения начальной конфигурации, и этот выбор часто приводит к глобальному наилучшему решению. Однако это возможно для mdscale для остановки в конфигурации, которая является локальным минимумом критерия. Такие случаи можно диагностировать и часто преодолевать бегом mdscale несколько раз с различными начальными точками. Это можно сделать с помощью 'start' и 'replicates' аргументы пары имя-значение. Следующий код запускает пять реплик MDS, каждая из которых начинается с другой произвольно выбранной начальной конфигурации. Значение критерия распечатывается для каждой репликации; mdscale возвращает конфигурацию с наилучшим вписыванием.
opts = statset('Display','final');
[Y,stress] =...
mdscale(dissimilarities,2,'criterion','stress',...
'start','random','replicates',5,'Options',opts);
35 iterations, Final stress criterion = 0.156209
31 iterations, Final stress criterion = 0.156209
48 iterations, Final stress criterion = 0.171209
33 iterations, Final stress criterion = 0.175341
32 iterations, Final stress criterion = 0.185881Обратите внимание, что mdscale находит несколько различных локальных решений, некоторые из которых не имеют такого низкого значения напряжения, как решение, найденное с помощью cmdscale начальная точка.