В этом разделе описывается работа Toolbox™ статистики и машинного обучения quantile и prctile вычислить квантили и процентили.
prctile функция вычисляет процентили аналогично quantile вычисляет квантили. Следующие этапы вычисления квантилей также верны для процентилей, учитывая тот факт, что для одной и той же выборки данных квантиль при значении Q является тем же самым, что и процентиль при значении P = 100 * Q.
quantile первоначально назначает отсортированные значения в X к квантилям (0,5/n), (1,5/n),..., ([n-0,5 ]/n). Например:
Для вектора данных из шести элементов, таких как {6, 3, 2, 10, 8, 1}, отсортированные элементы {1, 2, 3, 6, 8, 10} соответственно соответствуют квантилям (0,5/6), (1,5/6), (2,5/6), (3,5/6), (4,5/6) и (5,5/6).
Для вектора данных из пяти элементов, таких как {2, 10, 5, 9, 13}, отсортированные элементы {2, 5, 9, 10, 13} соответственно соответствуют квантилям 0,1, 0,3, 0,5, 0,7 и 0,9.
Следующий рисунок иллюстрирует этот подход для вектора данных X = {2, 10, 5, 9, 13}. Первое наблюдение соответствует кумулятивной вероятности 1/5 = 0,2, второе наблюдение соответствует кумулятивной вероятности 2/5 = 0,4 и так далее. Пошаговая функция на этом рисунке показывает эти кумулятивные вероятности. quantile вместо этого помещает наблюдения в средние точки, так что первая соответствует 0,5/5 = 0,1, вторая соответствует 1,5/5 = 0,3 и так далее, а затем соединяет эти средние точки. Красные линии на следующем рисунке соединяют средние точки.
Назначение наблюдений квантилям
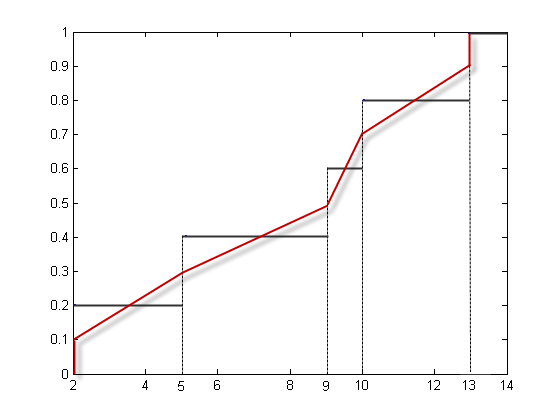
p квантили. Квантили X
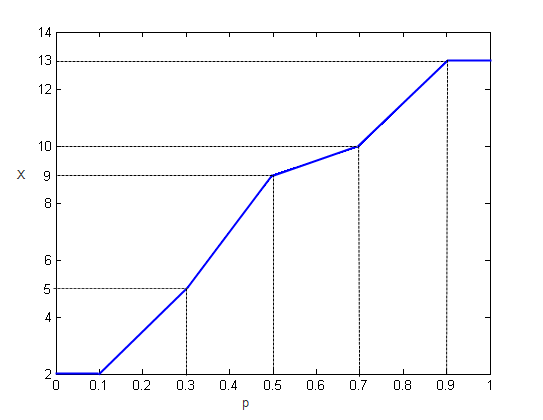
quantile находит любые квантили между значениями данных с помощью линейной интерполяции.
Линейная интерполяция использует линейные многочлены для аппроксимации функции f (x) и построения новых точек данных в пределах диапазона известного набора точек данных. Алгебраически, учитывая точки данных (x1, y1) и (x2, y2), где y1 = f (x1) и y2 = f (x2), линейная интерполяция находит y = f (x) для данного x между x1 и x2 следующим образом:
x1) (y2 − y1).
Аналогично, если квантиль 1,5/n равен y1,5/n и квантиль 2,5/n равен y2,5/n, то линейная интерполяция находит квантиль 2,3/n y2,3/n как
quantile присваивает первое и последнее значения X квантилям для вероятностей меньше (0,5/n) и больше ([n-0,5 ]/n) соответственно.
[1] Лэнгфорд, Э. «Квартили в начальной статистике», Журнал статистики образования. т. 14, № 3, 2006.